 Полная версия
Полная версияГравитация и эфир

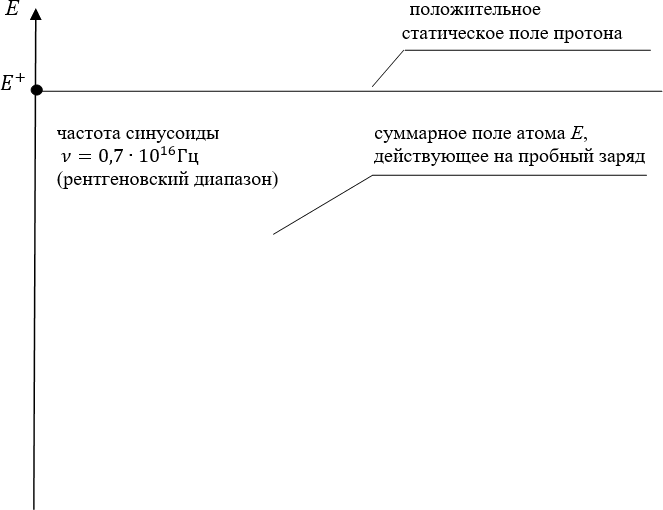
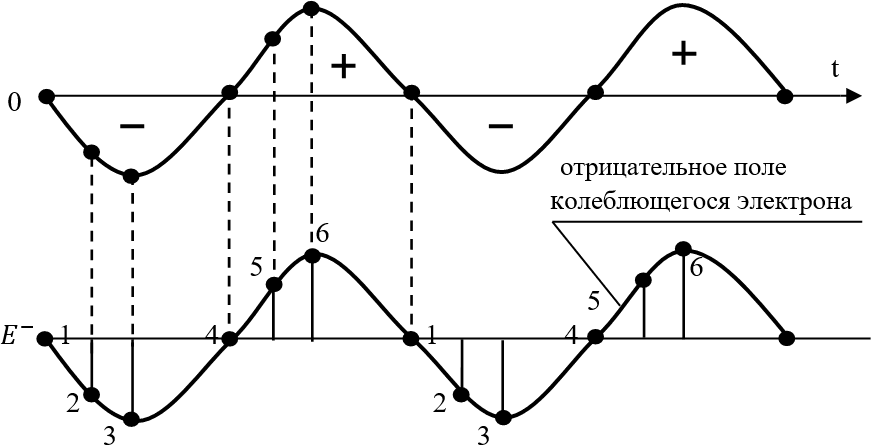
Рис. 21.8
Однако физики до сих пор никак не видят эти законные излучения нейтрального атома в его стационарном режиме и поэтому считают, что такой атом, поскольку он не возбуждён, то не излучает никакой энергии. Об этом же (о том, что физики не видят этих законных излучений атома) говорит один из двух фундаментальных постулатов Бора: «в стационарном режиме атомных орбит атом не излучает электрическое поле» (второй посулат Бора говорит об излучении атомом фотона при переходах электрона с более верхних орбит на более нижние).
Таким образом, квантовая физика видит, что даже те фотоны, которые современные физики «в упор не видят», имеют на самом деле ту «массу-энергию», которую, если бы эти физики очень захотели, то смогли бы запросто обнаружить в специальных опытах, и уже сейчас. Но они не мыслят в этом нужном для них направлении, а потому вообще не понимают с помощью своей любимой квантовой механики – а что там происходит с динамическими полями в ближней зоне каждого атома. Здесь «ближней зоной» можно даже считать размер атома газа по уровню, скажем, его сотой и даже тысячной орбиты, то есть по тем уровням, на которых электрон становится свободным от атома даже при весьма малом облучении последнего супер-мало энергичными фотонами, не говоря уже об облучении фотонами с энергиями в десятые или даже сотые доли электронвольта.
А теперь мы перейдём, наконец, к тем фотонам, которые уже «видел», но не знал пока действительной физики их излучения Макс Планк, перейдём к тем фотонам, которые Релей, Джинс, Вин и старинные спектроскописты воспринимали в виде интенсивностей «излучений», наблюдаемых ими в приборах-спектроскопах и для которых Бором была развита теория атомных переходов. Физики-спектроскописты естественным образом начинали свои исследования атомных спектров с тех фотонов, которые, во-первых, относились к видимому диапазону частот, во-вторых, имели аккурат те длины волн (порядка микрона), которые запросто можно было обнаруживать в дифракционных и интерференционных картинках с помощью простейших микроскопов.
Темы возбуждения атома мы уже касались (рисунки 21.5 и 21.7). На рисунке 21.9 показан процесс возбуждения двух атомов. Эти атомы возбуждаются из одного и того же состояния стационарного вращения электрона по первой круговой орбите. В обоих атомах начальной точкой возбуждения электронов является точка 1. Направление орбитального вращения электрона в левом атоме – правое (по часовой стрелке), в правом атоме – левое (против часовой стрелки), что, впрочем, не принципиально для сути процессов возбуждения. Пусть оба атома возбуждаются ударным способом короткими фотонами, следующими из точек 4, ускоряющими электроны по первоначальным дугам 1–2–3.
Мы можем уточнить, что из точек 4 на электроны точек 1 налетают не столько именно «фотоны», сколько «кванты энергии», причём в обоих случаях – «отрицательные» кванты энергии, отталкивающие электроны «вперёд» по их курсу, то есть положительно их ускоряющие. Энергия возбуждающих фотонов одинакова и такова, что в максимуме удалённости от ядра электроны касаются уровня второй атомной орбиты в точках 2.
Поскольку мы утверждаем, что электроны и протоны излучают кванты их полей всегда, где бы и когда бы они ни находились, то, следовательно, во время всего переходного процесса возбуждения атомов, в точку пробного заряда 5 будут следовать последовательные потоки квантов эфира, сгруппированные в короткие «кванты энергии» соответствующих полярностей. Причём от протонов в точку 5 будут следовать потоки положительных квантов энергии поля положительного «заряда» (протона) по лучу 0–5. Одновременно с этим, от движущихся электронов в точку 5 будут следовать потоки отрицательных квантов эфира, излучённых отрицательными «зарядами» (электронами) из всех точек сектора угла 1–5–3. Все эти потоки, как и сами электронные орбиты, жёстко поляризованы в плоскости книжного листа. Поскольку время движения электрона по дуге 1–2–3 составляет величину порядка
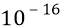
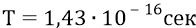
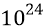
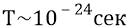
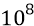
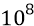
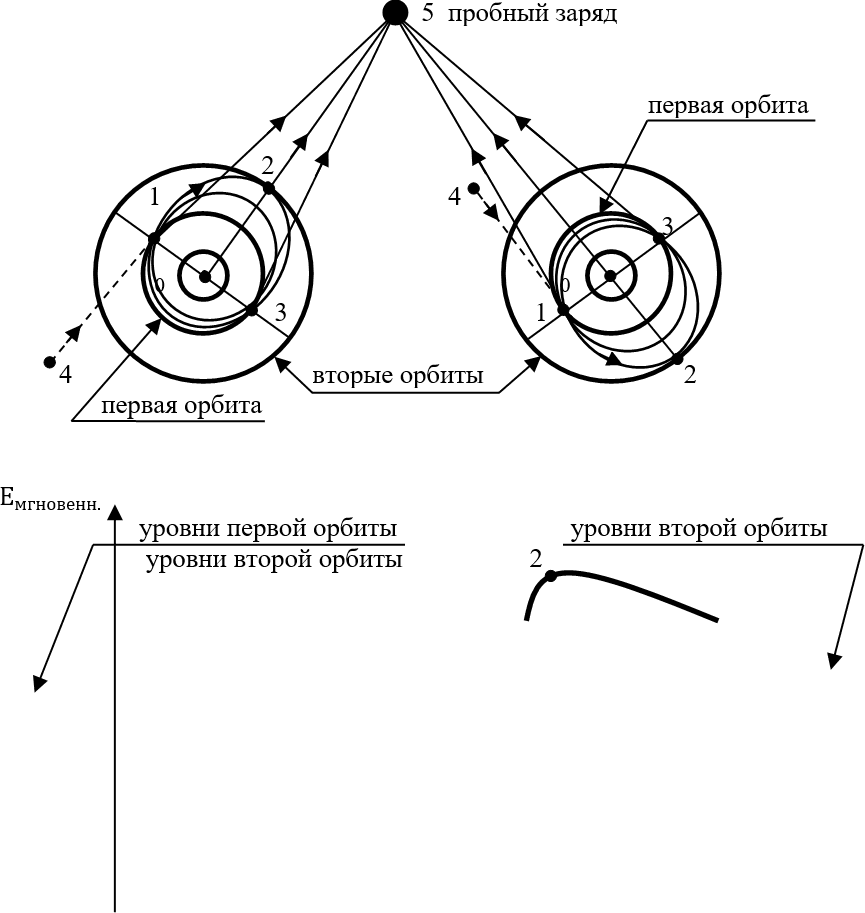

Рис. 21.9
Фактически на нижних диаграммах рисунка 21.9 представлена структура фотона, излучаемого атомом во время всего переходного (излучательного) процесса. В качестве огибающей этого сигнала мы выбираем закон изменения усреднённой напряжённости
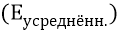
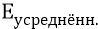

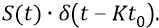
То есть в качестве
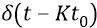

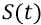
Последнее выражение определяет характер не сигнала, принимаемого в точке 5, но только сигнала излучаемого атомом «в точке излучения», то есть как бы «на выходе из атома». Но в точку приёма 5 этот сигнал придёт ослабленным пропорционально радиусу удалённости точки 5 от атома (R). Мы утверждаем, что закон изменения напряжённости поля по мере удаления фотона от источника (от атома) будет обратно пропорциональным не квадрату радиуса удалённости R, но обратно пропорциональным первой степени этого радиуса:
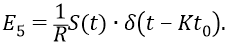
Все эти наши объяснения по поводу формул для излучаемых фотонов – это, грубо говоря, «объяснения на пальцах». В данной главе мы не ставим задачу досконального (математически грамотного) вывода – показа каких-то формул, но здесь впервые (и вот это «впервые» мы жёстко утверждаем) показываем школьнику (а заодно и профессионалам) примерную физику настоящего процесса излучения настоящих (эфирных) квантов, излучаемых атомом и называемых «фотоном». Про диаграммы можно приводить ещё очень много всяких подробностей. Но скажем сейчас главное. Мы утверждаем, что если временной сигнал усреднённой огибающей
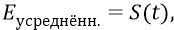
как функцию времени, подвергнуть далее преобразованию Фурье, то мы получим тот спектр того фотона, который излучил атом в данном его переходном процессе. И именно этот спектр видят всегда физики-спектроскописты, исследующие, например, нагретый газ водорода. В реальности они видят спектр, излучаемый не одним атомом (формулы Бора или Бальмера говорят о спектре единичного атома), но сразу многими атомами. То есть они видят как бы сумму многих и многих огибающих

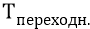
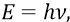
где частота ν будет соответствовать конкретной единичной спектральной линии, которую видят в микроскопы спектроскописты в виде-образе «длины волны». Эта «длина волны» – это расстояние между последовательными светлыми линиями (именно эти «светлые линии» видят в микроскоп исследователи). Измерив же это расстояние – как длину волны колебательного процесса, воспринимаемого «на глаз» в виде светлых и тёмных полосок в окуляре микроскопа, они вычисляют частоту этого процесса (как какого-нибудь светового луча данной частоты, падающего на экран – «измерительную дифракционную решётку»), по формуле:
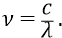
Ниже по тексту мы приведём конкретную методику вычисления конкретной спектральной линии.
Ещё раз, но уже – более понятно для школьника, то есть – без обращения к фурье-преобразованиям. Глядя на нижнюю диаграмму рисунка 21.9, мы видим то, как атом, быстро возбудившись, затем «медленно» успокаивается. При этом электрон движется по эллипсо-подобной орбите, медленно приближаясь «круг за кругом» к первой круговой атомной орбите. В переходном процессе левого атома электрон большую часть времени смещён в сторону пробного заряда точки 5, то есть атом суммой двух «зарядов» (электрона и протона) излучает всегда усреднённую отрицательную амплитуду поля E. В правом атоме электрон в среднем смещён дальше от точки 5, чем «стоящий на месте» положительный протон. Поэтому здесь атом излучает усреднённое положительное поле для точки 5. То есть в среднем за весь переходный процесс левый атом будет излучать в точку 5 только сплошь отрицательные кванты энергии, а правый атом – только положительные кванты энергии. Но спектроскописты никогда не видят излучение отдельного атома. Они воспринимают процесс излучения сразу многих атомов. А эти возбуждения большого количества атомов всегда подчинены закону больших чисел. Который говорит о том, что, например, в газе число «положительных» атомов, излучающих в данное мгновение положительный квант энергии в точку наблюдения за газом, с большой степенью точности равно числу «отрицательных» атомов, излучающих в эту же точку в это же мгновение «отрицательные» кванты энергии.
Поэтому общий поток фотонов, падающих на измерительный прибор физиков (например, на дифракционную решётку) будет состоять из большого количества положительных и отрицательных полуволн – как отдельных положительных и отрицательных «квантов энергии». И поскольку этих положительно-отрицательных пар квантов энергии будет, с большой степенью точности, одинаковое количество, то их сумму можно выстраивать-рассматривать в виде некоторого непрерывного (а на самом деле – чётко прерывного) синусоидального сигнала. Частота этой суммарной синусоиды будет соответствовать двум полу-периодам огибающей переходного атомного процесса. То есть полупериод этой синусоиды (именно полупериод, а не полный период) будет говорить о том, за какое время успокаивается переходный процесс после каждого возбуждения каждого конкретного атома.
Но чем могут быть вызваны те источники возбуждений в газе, которые в виде квантов энергии у нас на рисунке налетают на электроны точек 1 из точек 4? В простейшем случае они могут быть вызваны, например, процессами столкновений отдельных атомов в газе водорода. Атомы сталкиваются друг с другом своими отрицательными «электронными облаками». То есть к орбитальному электрону данного атома сначала приближается орбитальный электрон другого атома, который излучает в сторону первого (в ближней зоне между двумя близкими почти соприкасающимися атомами) свой «квант энергии» отрицательной полярности, то есть тот квант, о котором мы говорили в самом начале пояснений, касающихся рисунка 21.9.
Примерно такая же качественная картина возбуждений атомов будет и в любом нагретом веществе, включая вещество, например, металлов. Только там атомы, грубо говоря, «стоят на месте». Но между ними постоянно бегают внутри металла гигантское количество всевозможных квантов энергии (фотонов), всегда поддерживающих абсолютно все атомы металла в тех или иных возбуждённых состояниях. Причём при данной температуре эти возбуждённые состояния атомов по любому выделенному там линейному направлению носят строго периодический характер. То есть в любом выделенном направлении излучается свой определённый поток своих особых квантов энергии, говорящих об особых переходных процессах атомов металла в данной цепочке данного направления в структуре металла.
Таким образом, мы видим, что квантовая физика (как классическая теория) способна вернуть физиков из их вероятностной квантовой механики к временнóму описанию всех процессов, происходящих в любом участке любого вещества. Причём она может это выполнить досконально точно для любого выделенного дискрета времени изучаемого процесса.
Итак, мы утверждаем, что в любом случае любой фотон, излучаемый атомом в любом режиме работы атома (стационарном или возбуждённом) представляет собой сложный радиотехнический сигнал с АФИМ модуляцией (амплитудно-фазово-импульсная модуляция). Все попытки чистых математиков, не знакомых или плохо знакомых с радиотехникой, приводили и приводят их к непониманию того, чем является у Природы обычный фотон обычного света, мириадами фотонов которого мы окружены в каждую секунду нашей жизни. Если же к этому добавить главный фактор непонимания физиками фотона, а именно то, из чего у Природы сделан фотон (из квантов-частиц эфира), то одно только это непонимание фундамента квантовой физики даёт красноречивое объяснение причины жестокого кризиса, поразившего физику в последний век её развития.
Амплитудная модуляция излучаемого фотона проявляется в том, что на самом деле амплитуда отрицательных квантов, излучаемых колеблющимся электроном вокруг точки «равновесия» неподвижного протона, периодически меняется в точке приёма АФИМ сигнала (в точке 5). На каждом круге колебания электрона он: то приближается к точке 5, то удаляется от неё. У нас, в нашем грубом выражении-формуле эта амплитуда колебаний заключена составной частью в члене
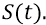
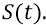

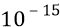
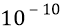
Фазовая модуляция в АФИМ фотоне – это общий случай частотной модуляции, поскольку частота – это
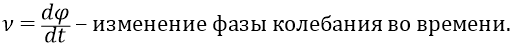
Огибающая усреднённой напряженности поля, излучаемого атомом
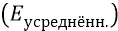
Импульсная модуляция АФИМ фотона – это заполнение каждого полупериода синусоиды δ-функциями (дельта-функциями), то есть отсчётами амплитуды очень короткой по времени длительности каждого из них, следующими через интервалы, равные периодам собственных вращений излучающих «зарядов» (протона и электрона). Эти отсчёты амплитуд следуют примерно через

Таким образом, мы теперь прекрасно видим, что любой свет на самом деле состоит не из «волн энергии» или даже (ближе к физике) не из «волн напряжённости» поля какого-нибудь излучателя этих «волн», но он состоит только из потока квантов эфира, сгруппированных источником (атомом) в «кванты энергии» – как в согласованные порции согласованных квантов эфира, несущих на себе, с собой энергию этого кванта. Эта энергия каждого такого кванта может выполнить ту или иную работу тогда, когда «квант энергии» (как «порция энергии») упадёт на какой-нибудь предмет. Далее этот «квант энергии» (на самом деле – поток-череда квантов эфира) может: либо отразиться от предмета (от электронных облаков его, предмета, атомов); либо углубиться вглубь «атомной решётки» этого тела-предмета и там – то ли упруго рассеяться на атомах, то ли возбудить эти атомы, ещё более рассеиваясь на них (то есть «поглощаясь» в веществе, как о том говорят физики).
Даже свет «монохроматического» лазера – как свет одной строго определённой «частоты» (например, зелёного луча лазера) не состоит ни из каких «синусоид» монохроматической частоты. Но он состоит только из отдельных «квантов энергии» – как отдельных полу-волн, возникающих при излучении атома активного вещества того же, например, лазера. Если далее луч лазера падает на любую атомную гладкую поверхность любого вещества (например, металла), то этот свет мы видим только потому, что он отражается от металла к нам в глаза или в объектив того микроскопа, в который мы смотрим, наблюдая за поверхностью металла потому, что от разных участков этой поверхности к нам в глаза летят потоки отражённых квантов энергии (фотонов).
Почему, глядя в микроскоп, мы видим всегда чередующиеся светлые и тёмные полоски отражённого к нам света? Физики не смогут грамотно ответить на этот простой вопрос школьника. Мы же говорим о том, что свет, как мы выяснили, состоит из положительных и отрицательных квантов энергии – как положительных и отрицательных (как бы) «полуволн» некоего «синусоидального» (одной частоты) монохроматического света. Но поскольку «квант энергии» видимого диапазона (как результат переходного процесса атома-излучателя) имеет порядок частоты повторения –
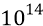
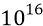
Таким образом, глядя в микроскоп, мы видим (и все физики тоже видели) действительный волновой процесс. Но он состоит, на удивление физикам, не из каких ни «синусоидальных» непрерывных волн, но только из прерывных потоков квантов эфира. Макс Планк в своей теории теплового излучения называл эти «прерывные потоки» (как мы их называем) по-своему – «порции энергии» или «элементы энергии». Ни Планку, ни физикам его времени, признавшим, тем не менее, его теорию, было абсолютно не понятно то, что атом излучает прерывные «порции энергии», но далее эти порции обязаны были распространяться в виде волны, иначе никак нельзя было объяснить никакие интерференционные и дифракционные эффекты, наблюдаемые физиками в многочисленных опытах. У нас эти порции квантов в виде «квантов энергии» распространяются от источника их излучения, далее – до поверхности падения луча и ещё далее (часть из них) – к нам в глаза, в качестве отразившихся «фотонов». Весь путь этих «фотонов» – только продолен – вдоль распространения луча света. То есть фотон – это продольный «сигнал», несмотря на то, что он же является волной.
Какой главный вывод можно сделать из проделанной нами здесь работы? Мы только что показали школьнику, что свет на самом деле состоит из корпускул вещества (эфира), движущихся в пространстве всегда только продольно, как думал об этом же ещё Ньютон. Но в то же время, как мы только что показали, этот поток квантов-частиц ведёт себя в пространстве (как макро-процесс) как волновой процесс, со всеми вытекающими из этого последствиями.
То есть, как видим, классическая квантовая физика «запросто» разрешает одну из самых загадочных проблем физики двух последних веков – «корпускулярно-волновой дуализм». На квантовом уровне продольный поток частиц ведёт себя как электромагнитная волна. При этом квантовая физика не отметает «поперечную волну Максвелла». Но просто она превращает такую волну в макро-процесс, запросто объясняемый на квантовом уровне: согласованными по фазе потоками многих и многих частиц материи, которые наши физики (скажем грубо) прошляпили, и которые у квантовой физики называются электромагнитными квантами – частицами эфира.

