 Полная версия
Полная версияГравитация и эфир
Но у электрона-частицы, как у единичного не релятивистского тела, не может быть никакой «потенциальной» энергии. То есть когда физики, в связи с атомом, начинают говорить о потенциальной энергии, то школьник должен чётко понимать, что они теперь говорят не об энергии электрона, но об энергии атома – как об энергии физической системы, состоящей из двух тел: из электрона и из ядра атома (из единичного протона в простейшем атоме водорода). Только у системы тел бывает «потенциальная энергия». Например, когда камень падает на землю, то, хотя физики жаргонно и говорят, что мол «поднятый над землёй камень имеет потенциальную энергию», но думают при этом обязательно о системе тел: о камне и о Земле, в потенциальном гравитационном поле которой падает камень. Поэтому Бор в своей теории, хотя и говорит кое-где (мы специально по этому поводу не исследовали первоисточники) о «потенциальной энергии электрона», но думает обязательно «о потенциальной энергии атома» – как системы тел. В выводах Бором его формул присутствуют оба типа энергий, из которых складывается полная энергия атома: присутствует кинетическая энергия (естественно – только электрона, ну не атома же) и присутствует потенциальная энергия – жаргонно – того же электрона, а на самом деле – атома.
А теперь вернёмся к выражению физиков, взятому нами в кавычки: «Когда электрон находится в атоме, то у него (выделено нами) энергии меньше, чем когда он свободен». Вот здесь сдвинутая шкала физиков явно запутывает школьника.
– Как же так, – думает школьник, – это получается, что чем глубже электрон «ныряет» в нижние атомные орбиты, тем у него там энергии меньше? Но я чётко помню о том, что кинетическая энергия тела, падающего в потенциальном поле, возрастает. То есть, например, у планеты Меркурий, самой близкой к Солнцу, самая большая скорость среди других планет. А это значит, что у какой-нибудь «единицы массы» тела Меркурия кинетическая энергия больше, чем у такой же «единицы» массы Венеры и тем более больше, чем у аналогичной «единицы» массы, кружащей в составе Земли по орбите Земли. То же и у электрона: чем «ниже» он скатывается по орбитам, стремясь в поле ядра к своему протону, тем больше на этих нижних орбитах его скорость, а значит, тем выше его кинетическая энергия. И наоборот, чем выше он поднимается по орбитам по возрастающему радиусу верхних орбит, тем меньше у него там скорость, а следовательно, тем меньше его кинетическая энергия. И если бы в природе существовали бы атомы с какими-нибудь «тысячными» орбитами, то там на них электрон, поднимаясь «наверх» всё больше и больше, терял бы свою скорость всё больше и больше, а значит, терял бы свою кинетическую энергию. И наконец, на какой-нибудь очень высокой орбите он настолько бы потерял свою скорость, что почти перестал бы двигаться по именно «орбите» такого гигантского атома, но его движение (еле уже заметное) можно было бы считать свободным от атома. В пределе, этот электрон мог бы вообще остановиться-зависнуть «над ядром». И тогда бы его кинетическая энергия превратилась в действительную нулевую. То есть он бы никуда не двигался: ни около ядра атома по касательной, намекая при этом на какое-то движение по «виртуальной», в таком случае, орбите; ни падая в сторону ядра, по причине полного разрыва с прежним ядром, около которого он раньше вращался. И можно ли при этом считать, что у системы тел есть какая-то «потенциальная» энергия, когда сейчас и самой-то системы уже нет как нет, поскольку электрон теперь полностью от неё свободен? То есть физики-то, как я понимаю (напоминаем, что это – мысли школьника), хотели бы мне в этом случае сказать, что электрон-де теперь обладает, хотя и нулевой кинетической энергией, но зато максимально возможной «потенциальной» энергией. Интересно, какой же такой «потенциальной» он в этом состоянии обладает?
Мы видим, что школьник, рассуждая логически, самостоятельно понял то, что электрон, далеко улетевший по каким-либо причинам от атома (от ядра – протона) не обладает там никакой уже потенциальной энергией системы «ядро-электрон». Физики это тоже прекрасно понимают. Они это понимали ещё задолго до исследования ими атомной системы, ещё тогда, когда были выведены законы электростатики. Потому что о самой потенциальной энергии заряда (электрона, а мы скажем – о потенциальной энергии не «заряда», но системы, состоящей из двух зарядов) можно говорить лишь тогда, когда один «заряд» (электрон) находится в потенциальном поле другого «заряда» (протона) и наоборот: когда протон находится в потенциальном поле электрона. Но поскольку рассматривается та система, в которой не ядро атома (протон) падает на электрон, но электрон падает на протон, то даже школьнику ясно, что такая система отличается по своим особенностям от, например, потенциальной системы «камень-Земля». В чём главном отличаются эти системы? В системе «камень-Земля» камень всегда находится не только в сильном гравитационном поле Земли, но практически в одном и том же сильном поле, лишь слегка отличающемся от положения поднятого камня и камня, лежащего на Земле – как на подставке, на которую упал камень. Если убрать эту подставку (поверхность Земли), то камень продолжит падать в потенциальном гравитационном поле Земли к её центру. Но у поднятого над поверхностью камня фактически есть новая (другая) подставка (где он либо лежит, либо что-то его держит на ней «за верёвочку»), где его кинетическая энергия равна нулю. То есть в этой системе движение камня происходит между двумя «подставками», на каждой из которых у камня есть своя потенциальная энергия. Но для кинематики движения камня в потенциальном поле удобно одну из подставок считать как бы «нулевой». Физики, для того чтобы прозрачно объяснить школьнику суть закона сохранения энергии, прибегают к картинке коромысла (качелей или чашек рычажных весов). На одной чашке весов как бы находится потенциальная энергия камня; на другой – кинетическая энергия камня. Когда камень поднят на высоту и там покоится, то его потенциальная энергия – максимальна (мы опять «жаргоним» вместе с физиками, говоря о потенциальной энергии одного тела, а не системы тел – как надо говорить правильно), а кинетическая энергия в верхнем положении равна нулю. В момент же касания упавшего камня поверхности земли (а точнее – перед самым-самым этим моментом) его кинетическая энергия максимальна, а потенциальная равна нулю. Максимальная потенциальная энергия перешла в максимальную кинетическую, а общая энергия системы тел, следовательно, всегда остаётся прежней, одной и той же (если в системе нет потерь, скажем, на какое-нибудь «трение»). Всё понятно: закон – он и есть закон.
Но у атомной системы двух тел – тогда, когда электрон далеко оторван от атома (от ядра), обе энергии равны нулю: электрон как бы завис над ядром и никуда не движется (кинетическая его энергия – нулевая), по причине очень малого (нулевого) там поля, действующего со стороны протона атомного ядра (система по потенциалу поля находится как бы в разрыве, а следовательно, её потенциальная энергия тоже равна нулю) Да, даже там, на этой «высоте», всё же есть малое электростатическое поле протона, и поэтому электрон всё равно, рано или поздно, но начнёт падать на протон. Но практически удобно считать, что система разорвана, со всеми вытекающими последствиями для её потенциальной энергии.
Но «классические» физики любили доскональность во всех своих механических и немеханических системах. Это только потом, физики 20-го века, предавшие почти во всех своих делах классику (механику), вынуждены были (как наказание для них) убежать от этой доскональности. Доскональность же классиков, в их отношении к определению ими потенциальной энергии, была и философски, и даже математически – идеальной. Покажем это.
Возвращаясь к камню, поднятому над землёй, мы видим, что на какую бы высоту мы ни поднимали этот камень, он всё равно будет падать с этой высоты на Землю. Будет ли он падать на Землю, если мы перенесём его, скажем, в другую галактику? Будет. Почему? Потому что даже там до него всё равно долетят гравитационные кванты поля, излучённого Землёй в направлении камня. Да, практически он, находясь в другой галактике, никогда не упадёт на Землю под влиянием этого её поля. Потому что там это поле Земли будет перебиваться значительно более сильным полем той галактики. И только поэтому камень не упадёт на Землю. Но если оттуда убрать ту галактику, оставив там камень в одиночестве, а также убрать все другие гравитационные тела, которые обязательно в реальности располагаются в космосе между тем камнем и Землёй, то рано или поздно камень всё равно упадёт на Землю под влиянием её гравитационного потенциального поля. То есть потенциальная система двух тел сохранится. Почему? Потому что сохранится третье тело, которое участвует в этой потенциальной системе. Когда мы говорим о том, что это тело «участвует» в системе, то при этом сильно принижаем значение этого третьего тела. Потому что если бы его, этого тела, не было, то камень никогда не упал бы на Землю, если только его изначальный курс не был бы направлен «лоб в лоб» точно на Землю. И здесь мы подходим к самому главному, говоря о потенциальной системе. Любая потенциальная система состоит на самом деле из трёх тел: из двух – взаимодействующих и одного – «посредника» между ними. Но именно этот посредник всегда совершает непосредственную работу по взаимодействию двух других тел в системе.
Начиная со времён Фарадея, в физику прочно вошло понятие «поля» (электрического, магнитного). Правда, гравитационному полю в 20-ом веке явно не повезло. Это только мы в нашей философии, да дилетанты всех мастей продолжаем говорить о «гравитационном поле». Но физики в 20-ом веке заменили это поле (внимание, школьники!!!) – пространством. У них два гравитирующих тела стали притягиваться не полем, но …… пространством. Правда – смешно? То есть физики от Фарадея снова скатились к пустому пространству. Потому что оно у них (тогда, когда они говорят о гравитации) ничем теперь не заполнено. Если же физики скажут, что пространство у них заполнено какими-то «массами», то мы скажем, что между любыми их «массами» всё равно остаётся какое-то пространство, причём пустое пространство, раз уж там нет гравитационного поля.
Но старинные физики (ещё до «полей») тоже работали с телами в как бы пустом пространстве. Однако они тогда были похитрее «двадцатово-вековых» физиков. Не зная пока ничего про поля, они работали в пустоте, но с силами. У них все тела передвигались (со времён Ньютона) – силами. Причём великолепно передвигались: точь-в-точь по законам механики. Но в 20-ом веке на поле физики наступил…, простите – ступил, новый учёный – Альберт Эйнштейн. Он предложил физикам свою новенькую теорию (ОТО), в которой в отношении гравитации убрал – запретил все силы. И у него всю работу по перемещению гравитирующих тел стало выполнять пустое…, простите – математическое, пространство. Но мы с этого учёного в нашей философии не будем брать пример, но вернёмся к старинным учёным и к их «силам».
Итак, у тех мудрых и неспешных физиков всю работу по перемещению любых тел выполняли соответствующие силы. В гравитационных взаимодействиях, например, всю работу выполняли «силы тяжести». Но мы, в 21-ом веке, возьмём за основу их «силы тяжести», но дополним их гравитационным потенциальным полем, беря пример с фарадеевых электрических полей. То есть чётко остаёмся на поле классики. Тогда, возвращаясь к камню, поднятому над Землёй, мы будем говорить сначала о работе этих самых «сил тяжести», совершаемой на самом деле гравитационным полем Земли по перемещению – притягиванию камня в потенциальном поле к Земле. Здесь работает, в соответствии со вторым законом Ньютона, сила тяжести:
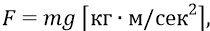
где
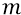
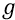
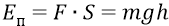
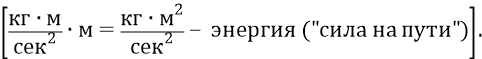
Здесь h – это высота поднятия камня над землёй, когда он падает с этой высоты h на подставку – Землю
Эту величину
Но теперь перейдём к общему случаю нахождения – движения тела в потенциальном поле Земли, когда тело падает (а мы скажем – передвигается полем Земли) с высоты
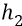
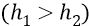
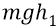
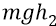
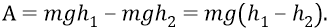
То есть здесь действует сила
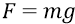

Далее нам надо будет вспомнить о классических «консервативных силах». Старинные физики ещё пока не говорили о «работе потенциального поля Земли» по перемещению тела из точки с уровнем потенциальной энергии на высоте
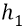
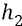
Но далее мы переходим к понятию изменения потенциальной энергии тела. А под этим изменением величины понимается разность между конечным (именно – конечным) и начальным значениями энергии тела. Так – по определению. Следовательно, для этого изменения (по определению) напишем формулу:

И далее, так как для сил тяжести
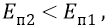
то работа сил будет отрицательна:
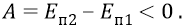
То есть если при перемещении тела с верхней (начальной) точки в нижнюю (конечную) работа сил тяжести естественна и, следовательно, положительна, то при перемещении тела из конечной (нижней) точки в начальную (верхнюю) работа этих сил «неестественна» и, следовательно, отрицательна. Так – у физиков с их силами тяжести.
Но наше объяснение должно быть проще, для понимания и запоминания школьником, когда мы будем говорить о тех же «силах тяжести», но как о «силах поля тяжести». Если поле притягивает верхнее тело (естественно) вниз, то работа такого поля будет положительна, но потенциальная энергия тела изменится отрицательно (упадёт). Если же над этим телом в этом поле совершается работа, неестественная работе самого поля, то есть тело поднимается снизу-вверх, то работа здесь будет совершаться (кем-то) отрицательная, хотя потенциальная энергия тела (от «нижнего» начального значения до «верхнего» конечного будет возрастать. В любом случае работа сил поля и изменение потенциальной энергии тела будут иметь противоположные знаки.
Теперь перейдём к атому. Там, в потенциальном электростатическом поле протона отрицательный электрон всегда будет падать в сторону положительного протона. Работу по притяжению электрона будет совершать поле протона. Причём поскольку эта работа будет естественна (в соответствии с законом Кулона – как с законом электростатики), то работа, совершаемая этим полем, будет положительной. Но изменение потенциальной энергии электрона (а мы скажем – системы «электрон-протон») будет отрицательным. То есть здесь, аналогично потенциальным силам тяжести (а мы скажем – силам гравитации), по мере падения «сверху» в сторону протона, потенциальная энергия системы будет естественно уменьшаться. Но где тогда эта энергия будет максимально возможной, раз она внутри атома уменьшается? Получается, что максимально возможной она будет где-то очень далеко от ядра атома, где электрон будет «висеть» над атомом очень «высоко». В пределе она будет максимальной только где-то в «бесконечности» от атома. Почему – в бесконечности? Потому что «лучи» электростатического поля любого «заряда» (протона – у нас) распространяются (не только в классике теории электростатики, но и в реальной природе эфира) очень-очень далеко, покуда существует этот эфир. Фактически (и мы это утверждаем в нашей философии) так оно и будет хотя бы потому, что какой-нибудь реальный квант – частица поля любого нашего протона вполне может добежать до краёв Метагалактики и даже забежать за эти края, притянув там какой-нибудь электрон в сторону, откуда квант начал свой бег; притянув электрон, если бы тот там был. Поэтому физики, предполагая о том, о чём мы только что сказали, присваивают статус обладания максимумом возможной электростатической потенциальной энергии – тому заряду, который удалён от поля заряда – излучателя на «бесконечность».
Но с другой стороны, как мы о том уже говорили ранее, на расстоянии – очень далёком от атома, фактически разрывается связь между электроном и протоном, то есть разрывается сама потенциальная система. Значит здесь, на большом удалении, потенциальная энергия электрона (на самом деле – системы) превращается в нулевую. То есть возникает как бы противоречие: энергия – нулевая и в то же время – максимально возможная. Но на самом деле никакого противоречия здесь нет, если мы вспомним о том, что потенциальная энергия может быть отрицательной. Ноль больше любого отрицательного числа. Это говорит о том, что приближаясь из бесконечности к атому, энергия электрона падает от нуля всё больше и больше в минусовую сторону. Но работа А потенциального поля протона (как мы помним) при этом естественна, и следовательно, положительна.
То есть в атоме мы снова приходим к картине изменения энергий, аналогичной картине подбрасывания камня над Землёй. И падающий в поле протона электрон, и падающий в поле Земли камень будут увеличивать кинетическую энергию. Кинетическая энергия принадлежит не полю, но самому телу – электрону и камню. И она для них будет только положительна, потому что определяется по фундаментальной классической формуле:
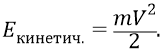
Здесь даже для любого V (положительного или отрицательного) она всегда будет положительна. Во всех выводах Бора она у него всегда – только положительна.
Потенциальная же энергия атомной системы будет всегда отрицательна. Так получается только потому, что в атомной системе мы сами выбираем для электрона самую «высокую» подставку, с которой он будет скатываться «вниз» – к ядру. «Вниз» – это всегда уменьшение потенциальной энергии – как уменьшение потенциальной возможности системы далее продолжать совершать работу. В этом смысле система будет обладать минимальной потенциальной энергией тогда, когда электрон упадёт на ядро, и там у него не будет уже никакой потенциальной возможности совершить работу за счёт потенциальной энергии системы, которой (этой энергии) там уже не будет. Но зато у электрона там будет возможность совершить работу за счёт его максимальной кинетической энергии – как энергии той же системы, но энергии, оставшейся там в одиночестве.
Таким образом (забегая вперёд) мы видим, что электрон в атоме, стартуя с любой стационарной орбиты, может подбрасываться, подобно камню, «вверх», на более высокие орбиты, увеличивая там свою потенциальную энергию (энергию системы), но уменьшая кинетическую энергию электрона. Но поскольку эта кинетическая энергия входит в суммарную энергию системы атома как положительная, то на верхних орбитах энергия атома, за счёт уменьшения там этой кинетической энергии, уменьшается. Но зато суммарная энергия там, на верхних орбитах, увеличивается за счёт увеличения потенциальной энергии системы. Какое изменение какой энергии будет превалировать? В результате, как мы ещё раз повторяем, энергия такой системы превратится в действительную нулевую. Это произойдёт тогда, когда электрон оторвётся от атома, истратив (превратив в ноль) свою кинетическую энергию, «зависнув» без движения над атомом, а потенциальная энергия превратится (по математике – в максимальную), а практически тоже в нулевую, поскольку произойдёт фактически разрушение системы, когда ни о какой потенциальной энергии такой разрушенной системы говорить (теоретически) будет можно, но практически – говорить не будет иметь смысла.
В реальном же мире любого атомного вещества никакой электрон никогда не «зависает» над атомом, лишаясь своей кинетической энергии. Даже тогда, когда возбуждённый каким-нибудь фотоном, он уходит от своего протона «вверх» по эллиптической орбите, то там, на самом «кончике» этой орбиты, он: или снова возвращается к протону, не теряя слишком сильно своей скорости на этом «кончике», но лишь поворачивая вектор своей скорости из радиального в касательный и затем – снова в (обратный) радиальный; либо тогда, когда «высоко» подброшенный, он этим «высоким» кончиком эллипса вторгается в поле другого атома, отрываясь от своего бывшего и падая в поле уже другого атома. Но для того чтобы мы увидели действительно свободный (освободившийся) от атома электрон, этот последний должен улететь не только от данного атома, но от поверхности какого-нибудь, скажем, металла достаточно далеко. Но даже там, будучи уже свободным, он, «задумав», например, снова вернуться в атомную решётку, из которой только что вылетел, никогда не теряет своей поступательной скорости, но «медленно» меняя скорость с радиального направления на тангенциальное и далее – снова на обратное радиальное, сохраняет свою кинетическую энергию на этом повороте на достаточно приличном её уровне.
Внутри же металла свободные (освободившиеся от какого-то данного атома) электроны вообще никогда не могут иметь низкой скорости, а следовательно, низкой кинетической энергии. То есть внутри металла, например, они всегда могут вылететь из атома и влететь в пределы другого с приличными скоростями, не сильно отличающимися от их скоростей на нижних атомных орбитах. Так может происходить только потому, что атомы складываются в атомную решётку не на уровне каких-нибудь тысячных орбит, где вылетающий электрон мог бы действительно заметно потерять свою скорость и кинетическую энергию, но соединяются на уровне уже единичных или, в худшем случае, на уровне номеров орбит, не превышающих десятка.
Мы только что говорили фактически о тех электронах, которые вырываются, например, из металла подогретого катода любой лампы накаливания. В старых ламповых приборах (телевизорах или радиоприёмниках) нити накала ламп всегда светились красным светом. Для чего нити накала (или они же – фактически катоды ламп) подогревались проходящим по ним достаточно большим током накала? Для того, чтобы перевести множество электронов на возбуждённые орбиты. Из теории фотоэффекта мы знаем, что из холодного металла можно выбивать электроны только ультрафиолетовыми фотонами, имеющими высокую энергию порядка энергии ионизации металла из состояния первой орбиты (10–13 эВ). Но в телевизоре мы не применяем никакой ультрафиолет. Но зато сильно подогреваем металл катода лампы, как бы переводя заранее его электроны с нижних уровней на более верхние, когда он может ионизироваться с них уже не ультрафиолетовыми, но фотонами видимого диапазона, и даже не «белыми» или «жёлтыми», но уже «красными», то есть не такими уж и энергичными. Но их энергии уже хватает на то, чтобы выбить электроны – не с нижних орбит (с нижних всё равно не получится), но с «подогретых» верхних. Что и происходило в электронных лампах с подогревающимися катодами. Причём в этих лампах существовала так называемая «сетка». Она располагалась «выше» катода, но ниже ускоряющего анода. На эту сетку подавался отрицательный потенциал по отношению к потенциалу катода, из которого вылетали «подогретые» электроны. И в лампах существовали (как вполне рабочие) такие режимы, когда электроны с катода вылетали, но потом, отталкиваемые отрицательной сеткой, они не прорывались через неё к аноду и, следовательно, не давали никакого анодного тока лампы (где располагалась полезная нагрузка). То есть в этих режимах около катода наблюдалось действительное электронное облако из вылетевших электронов, затем закруглявших свои траектории и затем снова падающих на поверхность металла катода (а эта поверхность всегда удерживает атомные электроны, сохраняя таким образом атомную решётку).

