
Полная версия:
Удивительные числа Вселенной. Путешествие за грань воображения
Все это противоречит нашей интуиции. Если гепард бежит по равнине со скоростью 70 миль (113 км) в час, а Болт преследует его со скоростью 30 миль (48 км) в час, то обычная логика подсказывает, что гепард каждый час будет увеличивать свой отрыв от спринтера на 40 миль (65 км) – просто потому, что его относительная скорость равна 70–30 = 40 миль в час. Но когда мы говорим о луче света, двигающемся по равнине со скоростью 299 792 458 метров в секунду, то неважно, как быстро бежит Болт, – луч света все равно будет двигаться относительно него со скоростью 299 792 458 метров в секунду. Свет всегда будет двигаться со скоростью 299 792 458 метров в секунду[6] – относительно африканской равнины, относительно Усэйна Болта, относительно стада паникующих антилоп-импал. Это действительно не имеет значения. Мы можем подвести этот итог в одном твите:
Скорость света – это скорость света.
Эйнштейну бы это понравилось. Он всегда говорил, что его идеи следовало бы именовать теорией инвариантности, сосредоточив внимание на их наиболее важных аспектах: постоянстве скорости света и инвариантности законов физики. Ироничное название «теория относительности» придумал немецкий физик Альфред Бухерер, критиковавший работу Эйнштейна. Мы называем ее специальной теорией относительности, чтобы подчеркнуть тот факт, что все вышеизложенное применимо только к равномерному движению, или движению без ускорения. Для ускоренного движения (когда гонщик «Формулы-1» нажимает на газ или ракета взлетает в космос) нам нужно нечто более общее и глубокое – общая теория относительности Эйнштейна. Мы подробно поговорим об этом дальше, когда погрузимся на дно Марианского желоба.
А пока давайте придерживаться специальной теории относительности Эйнштейна. В нашем примере предполагается, что Болт, гепард, импала и луч света двигаются с постоянной скоростью друг относительно друга. Их скорости могут различаться, но не меняются со временем, и главное, несмотря на эти различия, все видят, что световой луч удаляется от них со скоростью 299 792 458 метров в секунду. Как мы уже видели, это общее представление о скорости света, безусловно, противоречит нашему повседневному пониманию относительных скоростей, когда одна скорость вычитается из другой. Но причина здесь только в том, что вы не привыкли путешествовать со скоростями, близкими к световой. Иначе вы бы смотрели на относительные скорости совсем по-другому.
Проблема во времени.
Видите ли, вы предполагали, что в небесах есть какие-то огромные часы, которые сообщают нам точное время. Возможно, вы не считаете, что предполагаете такое, но это именно так, – в частности, когда начинаете вычитать относительные скорости, руководствуясь тем, что считаете здравым смыслом. Мне жаль вас разочаровывать, но эти абсолютные часы – фантазия. Их нет. В реальности существуют лишь часы на вашем запястье, часы на моем запястье или часы на Boeing 747, летящем через Атлантику. У каждого из нас есть собственные часы, собственное время, и показания этих часов не всегда совпадают, особенно если кто-то мчится со скоростью, близкой к световой.
Предположим, я поднимаюсь на борт Boeing 747 и вылетаю из Манчестера. К тому моменту, когда самолет достигает побережья в Ливерпуле, он летит со скоростью несколько сотен километров в час. К легкому раздражению других пассажиров, я решаю подкинуть мяч в салоне на пару метров. Моя сестра Сьюзи (живущая в Ливерпуле) находится на пляже, когда самолет двигается над ней, и, с ее точки зрения, мяч пролетает значительно дальше – примерно двести метров или больше. На первый взгляд кажется, что такая ситуация не требует серьезного пересмотра нашего повседневного представления о времени. В конце концов, быстро летящий самолет просто переносит мяч с собой, и, естественно, Сьюзи видит, что он перемещается намного дальше. Но теперь поиграем в аналогичную игру со светом. Я ставлю вертикально на полу салона фонарик и включаю его: вертикальный луч света двигается перпендикулярно направлению движения самолета. Через какое-то очень короткое время я вижу, как свет достиг потолка салона. Если бы Сьюзи могла заглянуть внутрь, она увидела бы, как свет распространяется по диагонали, поднимаясь от пола к потолку, но при этом также перемещаясь горизонтально вместе с самолетом.

Траектория светового луча в глазах Сьюзи на пляже
Для нее это расстояние по диагонали больше, чем то расстояние по вертикали, которое измерил я; следовательно, она увидела, что свет прошел большее расстояние, нежели увидел я. Однако свет и для нее двигался с такой же скоростью. Это может означать только одно: для Сьюзи свету потребовалось больше времени, чтобы пройти свой путь. Иными словами, с ее точки зрения, мир внутри самолета должен двигаться в замедленном темпе. Этот эффект известен как замедление времени.
Степень замедления зависит от относительной скорости – скорости моего самолета относительно сестры или скорости Усэйна Болта относительно его родителей на трибунах стадиона. Чем ближе вы к скорости света, тем больше замедляется время. Когда Болт бежал в Берлине, его максимальная скорость составляла 12,42 метра в секунду, а время замедлилось в 1,000000000000000858 раза[7]. Это рекорд для человека.
Существует и еще одно следствие замедления времени: вы стареете медленнее. Например, Усэйн Болт постарел примерно на 10 фемтосекунд меньше, чем все зрители на трибунах во время берлинского забега. Конечно, фемтосекунда – это не так уж и много (всего лишь одна миллионная доля от миллиардной доли секунды), но все же он постарел меньше, так что, вернувшись в состояние неподвижности, он прыгнул в будущее, хотя и совсем чуть-чуть. Если вы не очень хорошо бегаете, то для замедления времени можно воспользоваться механическими средствами, и есть все шансы, что у вас получится даже лучше. Например, российский космонавт Геннадий Падалка провел в космосе 878 дней 11 часов и 31 минуту на борту космических станций «Мир» и МКС, вращаясь вокруг Земли со скоростью примерно 28 000 километров в час. В результате ему удалось попасть в будущее на рекордные 22 миллисекунды раньше по сравнению с его семьей, оставшейся на Земле[8].
Однако вам незачем становиться космонавтом, чтобы путешествовать во времени таким образом. Таксист, который ездит по городу сорок часов в неделю в течение сорока лет, окажется на несколько десятых микросекунды моложе по сравнению с человеком, который просто сидит на месте. Если вас не впечатляют микросекунды и миллисекунды, подумайте, что может случиться с бактериями, оказавшимися на борту корабля Starshot, который ученые хотят направить к альфе Центавра. Starshot – детище венчурного капиталиста-миллиардера Юрия Мильнера, который планирует разработать аппарат с солнечным парусом, способный долететь до ближайшей к нам звездной системы со скоростью в 20 процентов от световой. Альфа Центавра находится от нас на расстоянии около 4,37 светового года, поэтому до окончания такого путешествия землянам придется ждать более двадцати лет. Однако для самого аппарата и безбилетных бактерий на его борту время замедлится до такой степени, что путешествие займет менее девяти лет.
В этот момент вы можете заметить кое-что подозрительное. Если наша отважная бактерия будет девять лет мчаться со скоростью в одну пятую от скорости света, то она пролетит менее двух световых лет, а это менее половины расстояния до альфы Центавра. То же и с Усэйном Болтом. Я сказал вам, что он бежал на 10 фемтосекунд меньше, чем вы думали, а поэтому в реальности он и преодолел меньшее расстояние. И это действительно так. С точки зрения Болта, дорожка двигалась относительно него со скоростью 12,42 метра в секунду, поэтому она должна была уменьшиться в длину примерно на 86 фемтометров (что соответствует размеру примерно 50 протонов). Вы можете даже поспорить, что он в каком-то смысле не совсем совершил забег. Для бактерии пространство между Землей и альфой Центавра будет двигаться очень быстро, и в результате оно сократится менее чем на половину своей первоначальной протяженности. Такое сокращение пространства или дорожки берлинского стадиона известно как релятивистское (или лоренцево) сокращение длины. Итак, вы видите, что бег не только уменьшает ваш возраст, но и помогает вам выглядеть стройнее. Если бы вы бежали со скоростью, близкой к скорости света, любой наблюдатель заметил бы, что вы расплющились, как блин, благодаря сокращению занимаемого вами пространства.
Тут есть еще кое-что, о чем вам следует побеспокоиться. Я только что сказал, что дорожка стадиона двигалась относительно Усэйна Болта со скоростью 12,42 метра в секунду. Следовательно, его родители двигались по отношению к нему с точно такой же скоростью. С учетом всего вышесказанного это означает, что Болт должен увидеть, как часы его родителей замедлились. Но это выглядит очень странно, потому что я уже сказал вам: родители Болта должны увидеть, как замедляются часы их сына. Однако на самом деле именно так и обстоят дела: как Уэлсли и Дженнифер видят своего сына в замедленной съемке (!), так и Болт тоже видит их в замедленной съемке. И вот тут есть один действительно тревожный момент: я ведь также отмечал, что Болт финишировал в забеге, оказавшись на 10 фемтосекунд моложе, чем был бы, если бы стоял на месте. Разве мы не можем перевернуть ситуацию и посмотреть на нее с точки зрения Болта? Для его родителей время идет медленнее, так почему они не могут меньше постареть? Кажется, у нас появился парадокс. Он известен как парадокс близнецов (обычно в его объяснении фигурируют близнецы), но, к сожалению, у Усэйна Болта нет близнеца. Впрочем, это неважно. Истина состоит в том, что именно Болт стареет меньше и остается чуть-чуть моложе. Но почему он, а не его родители?
Чтобы ответить на этот вопрос, нужно учесть роль ускорения. Помните: все, что мы до сих пор обсуждали, относится к равномерному движению, когда ускорение отсутствует. В те моменты, когда Болт бежит с постоянной скоростью 12,42 метра в секунду, он и его родители – инерциальные объекты. Это просто причудливый жаргонный термин, который сообщает, что они не ускоряются, на них не действует никакая дополнительная сила, ускоряющая их или замедляющая. Во всех таких случаях применяются законы специальной теории относительности, поэтому и Болт будет видеть своих родителей в замедленной съемке, и наоборот. Однако спринтер не бежит с постоянной скоростью на протяжении всего забега: сначала он разгоняется с нуля до максимальной скорости, а в конце снова замедляется. На отрезках, когда он ускоряется или замедляется, бегун не является инерциальным объектом (в отличие от своих родителей). Движение с ускорением – совершенно другое дело. Например, даже если запереть вас в каюте корабля без окон, вы однозначно сможете сказать, ускоряется ли корабль, потому что почувствуете силу, действующую на ваше тело. Слишком сильное ускорение может даже убить вас. Конечно, смерть Болту никогда не грозила, однако его ускорения и замедления было вполне достаточно, чтобы убрать эквивалентность между ним и его родителями. Такая асимметрия устраняет наш парадокс: более подробный анализ, где тщательно учитывается ускоренное движение бегуна, показывает, что немного меньше будет стареть именно Болт, а не его родители.
Важно понимать, что это не просто забавное развлечение с уравнениями. Это реальные эффекты, которые ученые уже измерили. Установлено, что быстро движущиеся атомные часы тикают медленнее, чем их стационарные аналоги; они «меньше стареют», подобно Усэйну Болту в Берлине. Еще одно свидетельство дала крохотная частица под названием мюон: у нее обнаружена «отсрочка смерти». Мюон очень похож на обычный электрон, вращающийся вокруг ядра атома, но примерно в двести раз тяжелее и живет гораздо меньше. Примерно через две миллионные доли секунды он распадается на электрон и маленькие нейтральные частицы, называемые нейтрино. В Брукхейвенской национальной лаборатории в Нью-Йорке проводится эксперимент, в ходе которого мюоны разгоняют по 44-метровому кольцу до скорости в 99,94 процента от световой. Если учесть известную продолжительность их жизни, можно ожидать, что мюоны до своего распада совершат только 15 кругов; однако каким-то образом они проходят примерно 438 кругов. Дело тут не в том, что у них как-то удлинилась жизнь (если бы вы двигались рядом с одним из мюонов с той же скоростью, вы бы все равно увидели, как он распадается через две миллионные доли секунды[9]), просто при движении на такой скорости длина окружности кольца уменьшается в 29 раз по сравнению с исходной. В результате мюон успевает пройти около 438 кругов, потому что на каждом круге из-за сокращения длины ему приходится проходить меньшее расстояние.
Сокращение длины и замедление времени помогают нам понять, почему ничто и никто (и даже Усэйн Болт) не может двигаться быстрее света. По мере того как Болт все ближе подбирается к скорости света, кажется, что его время замедляется до полной остановки, а расстояния, с которыми он сталкивается, стягиваются к нулю. Как можно еще больше замедлить время? Куда можно еще уменьшить расстояния? Просто некуда. Скорость света представляет собой некий барьер, и единственный разумный вывод состоит в том, что ничто и никто не может двигаться быстрее.
Ускоряясь и приближаясь к скорости света, Болт потребляет все больше калорий, пытаясь разогнаться все сильнее. Скорость света выглядит непреодолимым барьером, поэтому в конце концов его скорость начинает стабилизироваться, а ускорение замедляться. Чем ближе он к скорости света, тем труднее двигаться. Его инерция – сопротивление ускорению – становится все больше. В этом и состоит проблема с попыткой разогнаться до скорости света: инерция увеличивается до бесконечности.
Но откуда берется эта инерция? Единственное, что Болт привносит в систему, – это энергия, и именно она должна быть источником дополнительной инерции Болта. Энергия никуда не исчезает, она просто меняет свой вид, переходя из одной формы в другую. Таким образом, инерция должна быть какой-то формой энергии, и это должно быть истинно, даже когда Болт находится в покое. Хорошо то, что для Болта, находящегося в покое, мы точно знаем инерцию: это просто его масса, ведь чем он тяжелее, тем ему труднее двигаться. Масса и энергия являются одним и тем же – в соответствии с формулой Эйнштейна[10]: E = mc2. Ужаснее всего в этой формуле то, какое огромное количество энергии (Е) можно получить из массы (m) благодаря огромной величине скорости света (c). Усэйн Болт в состоянии покоя весит около 95 килограммов, и, если всю эту массу преобразовать в энергию, она окажется эквивалентна 2 млрд тонн тротила. Это более чем в 100 000 раз превышает энергию, выделившуюся при взрыве в Хиросиме.
Теперь поговорим о пространстве-времени.
Погодите. Что это? Откуда оно взялось? На деле все это время мы говорили о пространстве-времени. Сокращение длины. Замедление времени. В вышеуказанных примерах время и пространство растягиваются и сжимаются в идеальном тандеме. Поэтому неудивительно, что они должны быть связаны, оказаться частью чего-то большего. Родившийся в Российской империи и проработавший почти всю жизнь в Германии математик Герман Минковский был настолько вдохновлен идеями Эйнштейна, что совершил первый прыжок в пространство-время. Он заявлял: «Отныне пространство само по себе и время само по себе уходят в мир теней, и в реальности существует лишь их своеобразное сочетание». Довольно любопытно, что Минковский некогда учил молодого Эйнштейна в Высшей технической школе Цюриха, хотя вспоминал его как лентяя, которого никогда не волновала математика.
Что на самом деле Минковский подразумевал под пространством-временем? Чтобы понять это, мы должны начать с трех пространственных измерений. У пространства есть три измерения, потому что для определения своего положения вам нужно указать три независимые координаты: например, две ваши GPS-координаты и высоту над уровнем моря. Теперь взгляните на часы и запишите время. Подождите 30 секунд и снова посмотрите на часы. Те два момента, когда вы смотрели на часы, произошли в одной и той же точке пространства, но в разные моменты. Мы могли бы различать их, введя еще одну (временную) координату для отображения момента, в который произошло каждое из этих событий. Таким образом, у нас есть четвертая независимая координата – четвертое измерение. Соединим их и получим пространство-время.
Чтобы должным образом оценить элегантность концепции пространства-времени, следует подумать о том, как мы измеряем расстояния – сначала в пространстве, а затем в пространстве-времени. Расстояния в пространстве можно измерить с помощью теоремы Пифагора. Вы, вероятно, помните это школьное утверждение о прямоугольных треугольниках: квадрат гипотенузы равен сумме квадратов катетов. Однако эта старая теорема дает гораздо больше, чем вы могли решить поначалу. Чтобы понять почему, давайте сначала построим пару перпендикулярных осей, как показано на левом рисунке.
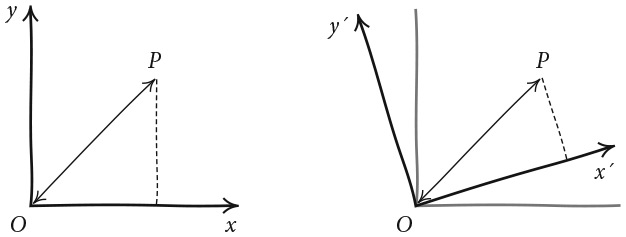
Относительно этих осей точка P имеет координаты (x, y), и по теореме Пифагора мы легко получаем, что она находится от центра координат на расстоянии
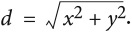
d2 = x2 + y2 = x2 + y2.
В этом и заключается настоящая прелесть теоремы Пифагора: расстояние остается неизменным даже при повороте координат.
Теперь о пространстве-времени. Минковский предложил нам объединить пространство и время. Конечно, в действительности нам хочется смешать три пространственных измерения с единственным временным измерением, но для простоты давайте рассмотрим одно пространственное, обозначенное координатой x, и соединим его со временем, обозначенным координатой t. Минковский определил, что для измерения расстояния d в этом пространстве-времени мы должны использовать странную форму теоремы Пифагора, которая задается формулой
d2 = c2t2 – x2.
Да-да, именно так: знак минус. Что все это означает? Мы к этому еще вернемся, но сначала нам нужно понять фрагмент c2t2. Мы хотим измерять расстояния и сразу констатируем очевидное: время – не расстояние. Чтобы превратить его в расстояние, нужно умножить его на какую-то скорость, а что может быть лучше скорости света? Это означает, что c2t2 можно рассматривать как единицу измерения квадрата расстояния, а это именно то, что нам нужно, когда мы думаем о теореме Пифагора. Теперь о знаке минус. Мера расстояния в пространстве-времени должна оставаться неизменной всякий раз, когда мы выполняем аналогичное вращение пространства-времени: когда проводим те преобразования, которые переводят нас между наблюдателями, движущимися друг относительно друга, – например, преобразование, которое переводит положение родителей Усэйна Болта в положение его самого. Такие «вращения» называются преобразованиями Лоренца; они кодируют растяжение времени и сжатие пространства, которые делают физику относительности такой удивительно причудливой. Таинственный знак минус имеет решающее значение для сохранения неизменными расстояний в пространстве-времени всякий раз, когда вы совершаете такой переход между инерциальными наблюдателями в относительном движении. Возможно, проще всего это увидеть для света, который движется в пространстве со скоростью x / t = c. Подставив это в формулу Минковского[11], мы увидим, что свет находится на нулевом расстоянии от начала координат в пространстве-времени. Начало координат остается на месте всякий раз, когда мы «вращаем» наши пространственно-временные координаты, и поэтому свет должен выглядеть одинаково для всех наблюдателей. Ничто не движется быстрее света в пространстве, но в пространстве-времени он вообще не перемещается ни на какое расстояние. Вот что делает его особенным.
А что насчет вас? Что вы делаете в пространстве-времени? Ну я предполагаю, что вы удобно устроились в кресле и читаете эту книгу. Что бы вы ни делали, мы знаем, что вы не движетесь в пространстве, определенном относительно вас самих, но движетесь во времени и поэтому должны двигаться в едином пространстве-времени. Насколько быстро? Что ж, берем формулу для расстояния при x = 0, получаем
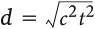
Соединив свои пространственно-временные координаты с расстоянием в пространстве-времени, Минковский начал строить удивительно изящную картину физики в терминах четырехмерной геометрии. Если записать на этом новом языке уравнения Максвелла, они обретают невероятно простую форму. Разделять пространство и время – все равно что смотреть на мир сквозь туман. Соедините их – и откроется мир удивительной красоты и простоты. Это и делает теоретическую физику таким замечательным предметом: чем больше вы понимаете, тем проще она становится. Возможно, это не более очевидно, чем использование Эйнштейном геометрии, чтобы победить силу гравитации и увидеть, что это обман. Эту историю мы расскажем попозже, снова используя замедление времени. Однако на этот раз мы не станем бежать вместе с Усэйном Болтом или мчаться сквозь космос с Геннадием Падалкой. Мы отправимся к центру Земли, где время идет чуть медленнее, чем на ее поверхности.
Бездна Челленджера«В действительности сильнее всего ощущение одиночества, осознание того, как крохотный ты опускаешься в это огромное, необъятное, темное, неизвестное и неисследованное место» – так сказал канадский кинорежиссер Джеймс Кэмерон. Эти слова свидетельствуют об ощутимом чувстве страха, о том, что ситуация не под контролем, что человек во власти чего-то большего. Эти слова были бы уместны в сценарии его самого известного фильма «Титаник», однако на самом деле они выражали эмоции режиссера после возвращения из Бездны Челленджера – самой глубокой из известных точек океанского дна, которая находится в Марианском желобе на глубине почти 11 километров ниже уровня моря. Кэмерон отправился туда 26 марта 2012 года в глубоководном аппарате Deepsea Challenger и провел три часа, исследуя этот чуждый мир: находясь в полном одиночестве в самой враждебной среде на планете.
Кэмерон стал первым человеком, который погрузился на такую глубину со времен группы ВМС США пятьдесят лет назад[12], и первым, кто сделал это в одиночку. Однако, возможно, примечательнее всего тот факт, что он вернулся из этого путешествия, прыгнув вперед во времени на 13 наносекунд.
Прыжок Кэмерона в будущее произошел не из-за высокой скорости, как у Усэйна Болта или Геннадия Падалки, а благодаря глубине погружения. Дело в том, что время замедляется еще и тогда, когда вы погружаетесь в гравитационный колодец, в данном случае – отправляетесь ближе к центру Земли. Это эффект общей теории относительности, объединившей релятивизм и гравитацию – вершины гения Эйнштейна. Поскольку Джеймс Кэмерон провел довольно много времени на глубине, у него накопилась впечатляющая величина гравитационного замедления времени.
Однако больше всех к центру Земли приблизился экипаж российской научно-исследовательской экспедиции «Арктика-2007».
2 августа 2007 года пилот Анатолий Сагалевич, полярник Артур Чилингаров и бизнесмен Владимир Груздев спустились в точке Северного полюса на дно Северного Ледовитого океана на борту глубоководного аппарата «Мир-1», оказавшись на глубине 4261 метра. Может показаться, что это гораздо меньше, чем глубина Марианского желоба. Однако Земля – не идеальная сфера, она имеет форму сплюснутого с полюсов сфероида, который слегка выпирает на экваторе. Поэтому аппарат «Мир-1» оказался гораздо ближе к центру планеты, чем Deepsea Challenger. Проведя полтора часа на морском дне, трое мужчин на борту аппарата переместились вперед во времени на несколько наносекунд. Помимо взятия образцов почвы и фауны, они установили российский флаг из нержавеющего титанового сплава. Это событие вызвало ожесточенные претензии со стороны других арктических стран, которые увидели здесь попытку объявить этот регион российской территорией. Россияне отрицали это, заявив, будто собирались просто доказать, что российский шельф простирается до Северного полюса, и сравнив это с тем моментом, когда астронавты «Аполлона-11» установили американский флаг на поверхности Луны.



