Все науки. №4, 2023. Международный научный журнал

Электрическое поле подвластно своему измерению благодаря такому понятию как напряжённость (12), что характеризуется воздействием на поля определённого заряда на некотором расстоянии на зондовый заряд благодаря силе Кулона (11).

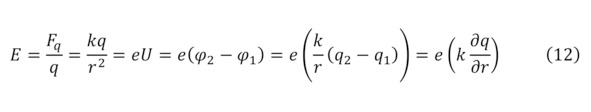
Такой же возможностью к вычислению обладает и магнитное поле, для него эта величина называется магнитной индукцией, измеряемая в единицах – Тесла, названные в честь великого и гениальнейшего сербского учёного своего времени Николы Тесла. Поскольку была ранее объяснена причина возникновения магнитного поля, то и её первое определение вычисляется через уравнения Максвелла и их следствия (13—16), подробнее о коих рассмотрено ниже.

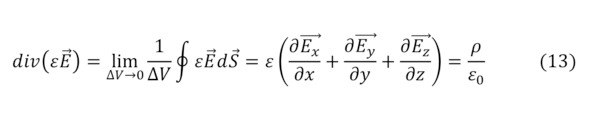
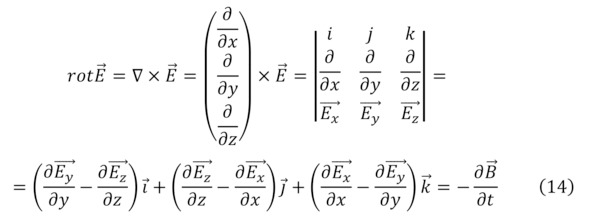
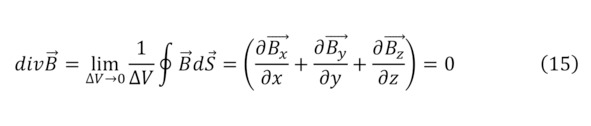
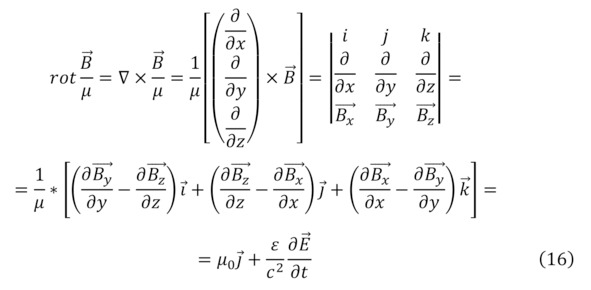
Кроме того, если сделать определённые исключения и благодаря свойству действия магнитного поля, в частности, и в статике, то закономерности для них будут подобны законам Кулона (17—18), а также в некоем поле будут следствием условия геометрии поля, что изначально предполагает теорема господина Андре Мари Ампера о циркуляции магнитного поля (19).

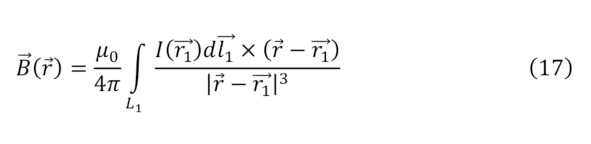
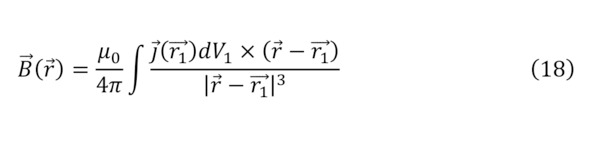
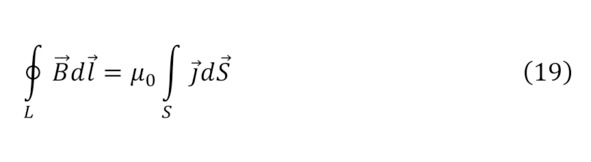
Однако, все эти параметры были приведены только для общего вида, но если обращаться к конкретным примерам, то в первую очередь стоит привести определение вектора магнитной индукции прямого провода с известным током и известном расстоянии от него определяется благодаря (20).

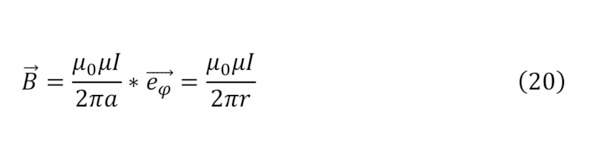
При этом важно отметить, что для определения вектора магнитной индукции необходимо определить магнитную проницаемость среды – это и есть параметр, демонстрирующий возможность того или иного материала проводить магнитное поле. Практически тоже самое можно сказать и о таком объекте как соленоид – самом настоящем электромагните, состоящий из спиралевидной проволоки и сердечника, как говорилось выше в самом начале описания.

И здесь, стоит присмотреться уже подробнее, ибо закономерность для определения магнитной индукции для соленоида выглядит следующим образом (21).

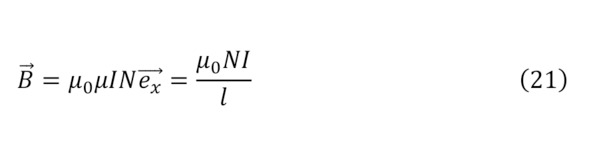
В данном случае, большую роль играет количество витков и с одной стороны, можно было бы сделать преобразование в (20), утвердив диаметр для спирали и учитывая все прошлые показатели для магнитной проницаемости, и протекающего тока (22), но эта закономерность будет не верной, поскольку в данном случае, образуется не прямолинейное, а именно вращательное электрическое поле, что создаёт непосредственно внутри соленоида прямое магнитное поле, приводя к верной формуле (21).

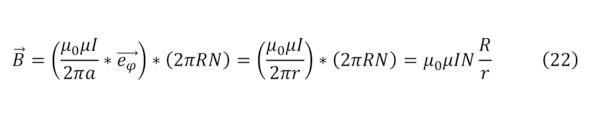
Перед продолжением, стоит отметить важный момент – если создаваемое поле является переменным по определению, оно создаёт переменное электрическое поле, которое в свою очередь опять создаёт паразитирующее магнитное поле, но уже противоположно расположенное для первого и сравнительно меньшее по величине. Такое дополнительное магнитное поле уменьшает эффективность первоначального магнитного поля, поэтому носит название паразитирующего, однако и оно создаёт паразитирующее поле для самого себя, а то в свою очередь для себя и т. д. В сумме, любое переменное магнитное поле состоит из большого количества малых молей, в лице своего родя рядов.

А поскольку магнитное поле, в отличие от электрического, всегда просто обязано быть замкнутым, оно замыкается вокруг соленоида, продолжаясь дальше. Именно таким образом и создаётся магнитное поле, которое обладает кроме показателя магнитной индукции, ещё и показателем напряжённости магнитного поля (23).

Но раз существует такая напряжённость и объяснён процесс создания при помощи зарядов магнитного поля, интересно рассмотреть обратный момент воздействия созданного магнитного поля на заряды. Тут стоит указать, что для образования магнитного поля можно воспользоваться также и природными магнитами, с изначально высокой концентрацией внутренних зарядов и их движений, за счёт природы самого сплава, либо при помощи прочих способов изменения формы электромагнита, к примеру, используя катушки Германа Гельмгольца для различных преобразований, а именно для суммарного модуля индукции магнитного поля из закона Био-Савара-Лапласа (24) или (25) для одиночного витка или для n витков (26), для случая что расстояние по оси от катушки до центра равняется половине радиуса (27), для двух катушек (28—29), или круглого соленоида, так называемого вида электромагнита – тороида (30), при том условии, что внутри него магнитное поле полностью отсутствует, а есть оно только внутри округлого проводника, на коем и намотана проволока.

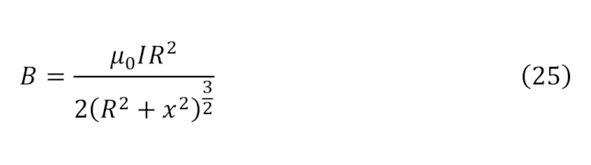
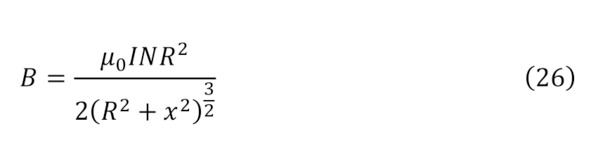
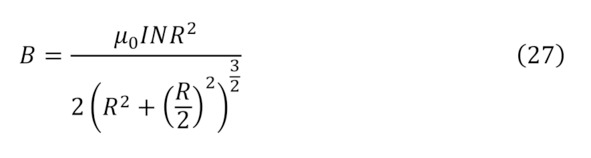
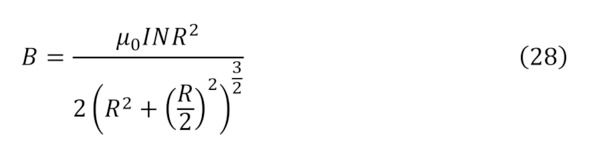
Таким образом, если свободный заряд попадает в магнитное поле, то он попадает под воздействие силы магнитной индукции под действием определённой силы Лоренца (31), под действием которого с учётом создаваемой центробежной силы (32), заряд начинает своё вращение с радиусом (33).

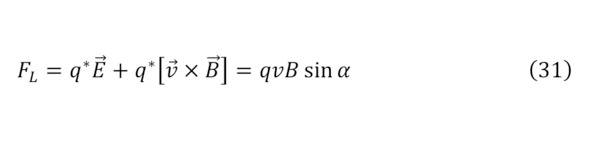
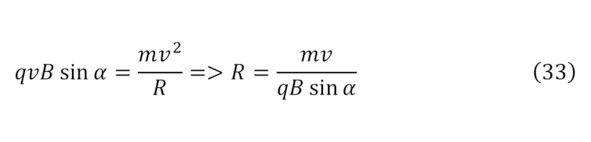
Более того, существует и релятивистская форма записи этой же закономерности (34—35).

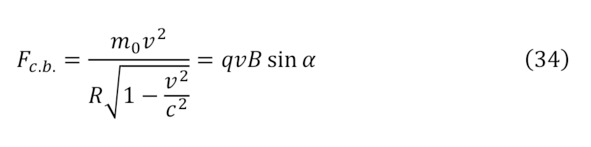
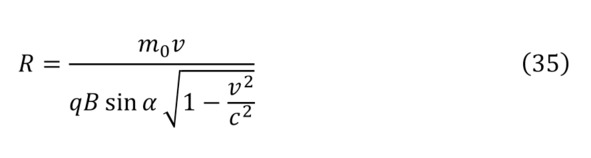
Но эти заряды при вращении опять же создают переменное электрическое поле, которое создаёт переменное магнитное поле – паразитирующее, а оно в свою очередь новое электрическое. То есть и в этом случае, ситуация с электромагнитном повторяется, что требует более подробного рассмотрения.

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.