Необычные размышления о…

На рис. 8.1 такая схема представлена.

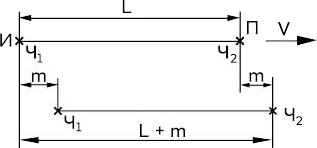
Рис. 8.1

где: И – точка испускания фотона;

П – точка приема фотона;

V – скорость перемещения материального объекта, например, галактики;

L – строго фиксированное расстояние между точкой испускания фотона и точкой приема фотона;

Т – время перемещения фотона из точки И в точку П;

m – перемещение материального объекта, например, галактики, в течение времени Т;

Ч1, Ч2 – часы, расположенные, соответственно, в точке И, а также, в точке П.

Верхняя часть схемы на рис. 8.1. отображает начальную фазу измерения – запуск фотона из точки испускания И.

Нижняя часть схемы на рис. 8.1. отображает конечную фазу измерения, когда фотон прилетает в точку приема фотона П. Перемещение фотона из точки И в точку П происходит в вакууме, с тем, чтобы скорость фотона была известной – 299 792 458 метров в секунду. В точках И, П размещены высокоточные атомные (цезиевые) часы Ч1 и Ч2. Расстояние между часами L тщательно измерено и остается неизменным в течение всего процесса измерений. Несколько слов о цезиевых часах.

Принцип действия таких часов основан на измерении излучения, возникающего при переходе электрона между двумя определенными энергетическими уровнями в атоме цезия-133. В течение одной секунды происходит 9 192 631 770 циклов колебаний такого излучения. Цезиевые часы производят подсчет таких колебаний. За одну наносекунду цезиевые часы насчитают приближенно 9,2 циклов колебаний. Если 1 метр разделить на 299 792 458 метров в секунду, то получим 3,335 наносекунд. За такое время фотон (свет) пролетает в вакууме расстояние в один метр. При измерении временного интервала в 3,335 наносекунд, цезиевые часы насчитают 30,68 циклов колебаний излучения. Ясно, что один километр фотон (свет) пролетает за 3335 наносекунд, а цезиевые часы сосчитают 30680 циклов колебаний излучений.

Эти примитивные расчеты мы приводим для того, чтобы читатель почувствовал, какой должна быть емкость счетчика и запоминающего устройства при цезиевых часах. Выбрали расстояние между часами (параметр L), равным одному метру, то необходимо будет запомнить 30,68 циклов. Но чувствительность и точность измерений будет низкой. При расстоянии в один километр между часами, чувствительность резко возрастает.

Следующая проблема при использовании цезиевых часов – это синхронизация их показаний или выставление единого нулевого показания (начала отсчета) на обоих часах. Можно указать на два способа синхронизации (выставления нулевого показания на обоих часах) часов. В первом случае, необходимо часы Ч1 и Ч2 расположить как можно ближе друг к другу и одновременно запустить на часах оба считывающих устройства, с помощью которых подсчитывают циклы колебаний излучения цезия.

Далее часы Ч1 и Ч2 можно переносить в пространстве, прикреплять их к чему-то, снимать с них показания, то есть, совершать с ними какие-то действия. При этом, количество сосчитанных ими циклов колебаний излучения цезия, в любой мгновенный момент времени на обоих часах будет одинаковым. Во втором случае, не обязательно часы помещать в единое место в пространстве. Часы можно разнести в пространстве. Но при этом необходимо точно знать расстояние между часами и обеспечить вакуумный канал между часами. В этом случае мы будем знать, что скорость света в таком вакуумном канале равна – 299 792 458 м/сек.

Проблема синхронизации времени (и часов) очень беспокоила Эйнштейна. Он считал, что синхронизировать часы можно только опираясь на принцип относительности. Поскольку, дескать, время всегда относительно и, якобы, абсолютного времени нет и быть не может.

Приступим к изложению методики измерения суммарного вектора скорости. Из точки И запускаем в сторону приемника П фотон (свет). Пусть, направление движения фотона совпадает с направлением перемещения нашего объекта (вектор скорости V). Если бы наш материальный объект (например, галактика, Солнце, Земля) не перемещался бы в пространстве, то фотон (свет) пролетел бы расстояние между часами Ч1и Ч2 (расстояние L) и долетел бы до приемника П за время: L/C. Но, пока фотон преодолевает расстояние L, наш объект переместится на какое-то расстояние: m = V*(L/C). В результате, фотон, прежде чем, достичь приемник П и часы Ч2, вынужден преодолеть расстояние: L+m за время:

T= (L+V*(L/C))/С; (8.1)

откуда, скорость объекта:

V= (T*C–L)/(L/C); (8.2)

где L – расстояние между источником испускания фотона и приемником испущенного фотона (приемник П) или расстояние между часами Ч1и Ч2;

Т – временной интервал, в течение которого, фотон преодолевает расстояние L+m;

С – скорость света в вакууме.

Временной интервал Т измеряется следующим образом: в момент запуска фотона, снимаются и запоминаются показания цезиевых часов Ч1, в момент прилета фотона (света) в точку П, снимаются показания часов Ч2.Определятся разность в показаниях часов Ч2 и Ч1. Эта разность – суть временной интервал Т. Величина параметра L с высокой точностью измеряется заблаговременно.

9. Измерение суммарной скорости перемещения галактики, Солнца и Земли

Таким образом, нам ничто не мешает измерить скорость суммарного движения галактики, Солнца и Земли, при нашем пребывании на поверхности Земли внутри галактики. И, вопреки утверждениям Галилео Галилея о том, что невозможно, находясь внутри объекта, который перемещается равномерно и прямолинейно (в инерциальной системе), отличить, пребывает ли он в состоянии покоя или находится в движении.

Оказывается, что даже можно измерить скорость такого объекта в любой, в практически мгновенный момент времени, построить график изменения скорости объекта во времени, и уже из графика узнать все о характере движения объекта. Напомним читателю, что точка испускания фотона (точка И) остается в неподвижной сетке и встраивается в неподвижную сетку (абсолютную систему отсчета). Кстати, абсолютный покой означает, что параметр m = 0. В этом случае, материальный объект неподвижен относительно любых точек испускания фотонов, испущенных и в прошлом, и в настоящем.

На нижней схеме рис. 8.1. мы наглядно видим, что точка И не перемещается вслед за фотоном, а, также, вслед за часами Ч1, что согласуется с нашими предыдущими рассуждениями. Попробуем оценить возможности наших измерений цезиевыми часами. Пусть, для определенности: L=1000 метров, V=1000 000 метров в секунду, тогда параметр m=3,3333 метра. Это то лишнее расстояние, которое вынужден пробежать свет, догоняя убегающие часы Ч2 и приемник света П. Напомним, что обусловлено такое убегание и лишнее расстояние перемещением галактики.

В параметре m заключена вся информация о скорости перемещения галактики, Солнца и Земли. 3,3333 метра свет пролетит за 11,0057 наносекунд. При этом, цезиевые часы насчитают лишних 101,2 циклов колебаний излучения. В цифре 101,2 – вся информация об измеряемой скорости V=1000 км/сек. Если L= 100 метров, то полезная информация будет включена в цифру 10,12 циклов. Мало. Если L=10 метров, то говорить не о чем (1,012 цикла). Цезиевые часы не помогут.

Для фундаментальных исследований расстояние: L= 1000 метров – не проблема. Но в подводную лодку или в космический аппарат, измерительный канал длиной в один километр – не всунуть. То есть для решения навигационной задачи необходимы дополнительные умствования. Но об этом чуть позже.

Мы рассмотрели случай, когда вектор скорости перемещения объекта полностью совпадает с направлением перемещения испускаемого фотона. На самом деле, применительно к суммарному вектору скорости галактики, Солнца и Земли, мы заблаговременно ничего не можем сказать об ориентации такого вектора в пространстве. То есть, мы заранее не знаем, куда направлять фотон (свет). В этом случае, мы должны обратиться к векторной математике. Построим прямоугольную (декартову) систему координат OXYZ. В начале такой системы координат поместим устройство, с помощью которого будем одновременно запускать три фотона в направлении трех осей системы координат, а также, в начале координат поместим часы Ч0. На трех координатных осях, на одинаковых расстояниях от центра такой декартовой системы координат, установим часы, соответственно, Чx, Чy, Чz.

Нетрудно видеть, что мы пролонгировали систему, на три оси декартовой системы координат. Если в центр такой декартовой системы координат поместить суммарный вектор скорости перемещения галактики V, ориентация которого в пространстве заранее неизвестна, то представляется возможным разложить такой вектор на его проекции по осям координат: Vx, Vy, Vz. Методика, изложенная выше, применительно к схеме на рис. 8.1, а также устройства (часы, источники испускания фотонов, приемники фотонов), установленные на осях системы координат OXYZ, позволяют измерить проекции Vx, Vy, Vz вектора скорости V.

По таким измеренным проекциям можно рассчитать величину вектора V, используя формулу векторной математики:

V = (Vx2 + Vy2 + Vz2)1/2. (9.1)

Ориентацию суммарного вектора скорости движения галактики, Солнца и Земли относительно осей нашей декартовой системы координат можно установить с помощью, так называемых, направляющих косинусов по формулам векторной математики:

COS X = Vx/V; COSY = Vy/V; COSZ = Vz/V. (9.2).

Напомним читателю, что время проведения измерения вектора скорости складывается из времени преодоления фотоном расстояния L (смотри рис. 8.1.), а, это 3335 наносекунд при L=1000 метров; времени считывания показаний часов – микросекунды; времени обработки (расчетов) информации в автоматическом режиме, на современных компьютерах – микросекунды.

В целом, процедура измерения вектора скорости V не превысит долей миллисекунды. Так что, процесс измерения – почти мгновенен. Если измерения приводить каждый час, то в течение суток получим 24 точки замеров, в течение года получим – 8760 точек замеров. Такие замеры можно использовать для построения графика изменения суммарного вектора скорости в течение определенного календарного срока времени, например, в течение года. Возможный вид такого графика может быть представлен на рис. 9.1. Если бы мы знали все о взаимном расположении в пространстве составных частей суммарного вектора скорости движения галактики, Солнца и Земли, то мы бы представили читателю более точную картину изображения такого вектора скорости. Поэтому приходится говорить о возможном виде такого графика. На рис. 9.1. по оси ординат отображена величина суммарного вектора скорости движения галактики, Солнца и Земли. Ось абсцисс – временная шкала.

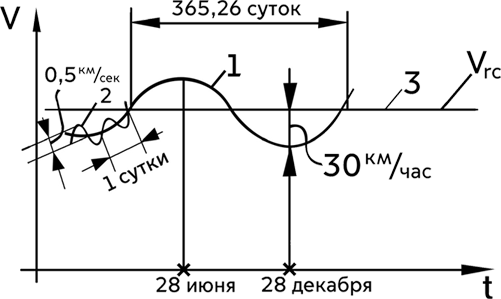
Рис. 9.1

где:

Vгс – суммарный вектор скорости, который образован путем векторного сложения скорости галактики и вектора линейной скорости перемещения Солнца, при его вращении вокруг центра галактики (постоянная, в течение 10 лет, составляющая вектора V);

1 – проекция траектории годового движения Земли вокруг Солнца на линию в пространстве – на вектор Vгс;

2 – проекция траектории суточного движения Земли вокруг земной оси вращения, на траекторию годового движения Земли. Такая проекция отображена не в масштабе, поскольку количество циклов суточных колебаний на годовой синусоиде должно быть 365. Такое количество суточных циклов не уместить на представленном рисунке;

3 – траектория суммарного перемещения в пространстве галактики и Солнца вокруг центра галактики. В течение 10 лет наблюдений за такой траекторией, ее имеет смысл рассматривать в качестве прямой линии. После 10 лет таких наблюдений, необходимо учитывать вращательное движение Солнца вокруг центра галактики.

Зададим вопрос: что будет, если мы станем испускать фотон в сторону, строго противоположную вектору скорости движения нашего объекта? В этом случае, до встречи с часами, фотон пролетит меньшее расстояние: L-m. Время, за которое фотон преодолевает такое расстояние, будет меньше, в сравнении с расстоянием: L+m.

Если, с помощью зеркала, заставить фотон перемещаться из точки испускания в точку приема и обратно – в точку испускания, то, в этом случае, фотон преодолеет расстояние: (L-m)+(L+m)=2L. Время преодоления такого двойного расстояния – соответствующее. При этом, мы видим, что реализация схемы измерения по принципу: перемещение фотона туда и обратно, ведет к потере параметра m. А это означает невозможность измерить скорость перемещения объекта, реализуя принцип измерения: туда и обратно. Так что, мы вынуждены измерять скорость движения объекта, путем перемещения фотона только в одну сторону, которая совпадает с направлением перемещения объекта. И это принципиально.

Реализация такого принципа позволяет нам понять, почему Альберт Майкельсон и его коллега Морли, не заявили об обнаружении светоносного эфира. Такое заявление они могли бы произнести, если бы сумели измерить скорость перемещения галактики и объяснить (интерпретировать) такое перемещение движением светоносного эфира. Но для этого, они должны были бы располагать соответствующим инструментарием. Например, цезиевыми часами, у которых высочайшая чувствительность измерения времени, и другими устройствами, которые позволяли бы им испускать и принимать испущенные фотоны, а в моменты испускания и приема этих фотонов, снимать и запоминать показания цезиевых часов.

В те далекие времена всего этого добра не было, и быть не могло. Цивилизации потребовались столетия, чтобы разработать и создать такое добро. Поэтому Майкельсон и его коллега воспользовались интерферометром, изобретенным Майкельсоном.

Свойством любого интерферометра является то, что у всех у них – один источник света. Если в интерферометр поместить два и более источника света, то становится невозможным получить когерентность циркулирующих в интерферометре лучей света. А, без когерентности лучей света, не получить интерференционную картину. Поэтому создатели интерферометров вынуждены встраивать в интерферометр зеркала, между которыми циркулируют лучи света, реализуя перемещение таких лучей по принципу: “туда и обратно”. А, это в принципе не позволяет измерить скорость объекта (галактики, Земли), с помощью, установленного в таком объекте интерферометра.

И, это – очень хорошо. Майкельсон и его коллега, 7 лет что-то там измеряли во всех пространственных направлениях, а также, в любые времена года и суток. И, слава богу, ничего не намерили. А, ведь, могли что-то намерить и объявить измеренное движением светоносного эфира. Настрой у них был такой: во чтобы-то не стало, найти светоносный эфир. Правда, они нашли нечто, на много более важное: установили независимость скорости перемещения света от скорости движения материального объекта.

Конечно, было бы не плохо, найти такого настойчивого Майкельсона и его коллегу, которые смогли бы на практике реализовать нашу идею измерения скорости галактики, Солнца и Земли. Только практика, а, не умствования, являются критерием истины. К сожалению, нам самим, не осилить такого рода практику. Одни, только цезиевые часы стоят столько, что даже подумать страшно. А, потому, продолжим наши умствования. И постараемся воспользоваться уже известными объектами. Например, лазерной интерферометрической обсерваторией (LIGO). Но об этом чуть позже. А пока, давайте попробуем определить пользу от всех наших возможных изысков.

10. Практическая польза от определения суммарного вектора скорости

В плане решения навигационной задачи и фундаментальной науки, просматриваются следующие возможные полезные достижения:

Как утверждалось выше, чтобы решить задачу навигации, необходимо втиснуть канал измерения суммарного вектора скорости внутрь подлодки или внутрь космического спутника.

То есть уменьшить канал измерения, хотя бы, до одного метра. Но, при этом, величина параметра m, в котором заключена вся полезная информация о скорости галактики, уменьшается до – 3,333 миллиметров. Свет пробегает такое расстояние так быстро, что цезиевые часы не успевают произвести хотя бы один цикл колебаний излучения цезия, соответствующий 3,333 миллиметрам.

Чтобы устранить такой недостаток, необходим дополнительный комплекс мероприятий. Во-первых, удлинить канал измерений, например, за счет применения оптоволоконных материалов. Скорость распространения света в оптическом волокне составляет – 160–180 тысяч км/сек., что уже хорошо, так как параметр m увеличивается (на одинаковой дистанции, которую пробегает свет) при уменьшении скорости света.

Правда, появляется дополнительная трудность: надо заранее знать длину оптоволокна и скорость прохождения света в нем. Потребуются дополнительные мероприятия, которые можно назвать заблаговременной калибровкой оптоволоконного канала. Суть такой калибровки состоит в том, чтобы измерить время прохождения света по оптоволоконному каналу, опираясь на принцип “туда и обратно” (чтобы исключить влияние скорости перемещения галактики). Зная время прохождения света по такому каналу, а также длину канала, можно определить скорость света в таком конкретном канале. Диаметр оптоволокна (или его толщина) принимает значения в диапазоне: 0,1–0,3 миллиметра. Если такой оптоволоконный провод, длиной в 1000 метров, намотать на барабан или на катушку диаметром – 30 сантиметров, то длина однослойной намотки оптоволоконного провода на такой катушке, составит 10–30 сантиметров. Что позволит втиснуть канал измерения длиной в 1000 и более метров в подводную лодку и в космический аппарат. При этом, достаточно будет одних часов, с помощью которых можно будет снимать показания, соответствующие моменту испускания фотона и моменту его фиксации приемником.

Однако, при этом, проблем не избежать. Дело в том, что когда свет перемещается внутри оптоволоконного витка, то пространственное направление перемещения света (фотона) в таком витке постоянно изменяется. В какие-то моменты времени направление света совпадает с направлением вектора Vгс (или его проекцией на направление света), в другие моменты времени – не совпадает. То есть, при движении света внутри одного витка, может быть реализован принцип: “туда и обратно”. В результате мы потеряем параметр m, а вместе с ним – информацию о скорости перемещения галактики. Единственный случай, когда такой потери не будет, это когда вектор Vгс перпендикулярен плоскости, проходящей через отдельно взятый виток оптоволокна. А, это значит, что ось катушки, на которую намотали оптоволокно, должна совпадать по направлению с вектором Vгс.

Читатель может сказать: мы же не знаем заранее – куда в пространстве направлен вектор Vгс. Да, это так. Но мы можем это узнать ранее изложенными способами, без применения оптоволокна, намотанного на катушку. Можем выяснить направление вектора Vгс в пространстве, запомнить его, например, с помощью визирования такого направления на известную звезду.

Или с помощью гироскопов, выставив на гироскопическую платформу катушку с оптоволокном таким образом, чтобы ее ось совпадала с заранее определенным направлением вектора Vгс. А, затем, остается катушку с оптоволокном удерживать в пространстве так, чтобы величина вектора Vгс оставалась неизменной (заранее определенной). Достичь этого можно, путем соответствующего подворачивания гироскопической платформы по углам тангажа, рыскания и крена. При этом катушка с оптоволокном будет участвовать в процессах по коррекции уходов гироскопов, в решении задач ориентации и определении пространственных и плоскостных параметров орбиты космического аппарата.

Неизменность положения вектора Vгс в пространстве, позволяет зафиксировать в пространстве плоскость орбиты и, тем самым, определить такие пространственные параметры, как наклонение орбиты и прямое восхождение восходящего узла, естественно, в сочетании с другими методами.

Если на вектор скорости Vгс спроектировать вектор орбитальной скорости спутника, то, станет возможным, определить параметры, характеризующие эллиптичность орбиты (величину большой оси, эксцентриситет). Чтобы избежать все эти сложности, необходимо на каждом витке катушки, в качестве полезной информации оставлять время прохождения света только в одном направлении. И игнорировать перемещение света в обратном направлении. В дальнейшем мы изложим один из таких способов.

10.1. Определение направления перемещения Туманной Андромеды

Если мы сумеем измерить и построить в пространстве вектор скорости перемещения нашей галактики, Солнца и Земли, то мы узнаем, в каком направлении и как движется наша галактика Млечный путь, например, по отношению к галактике Андромеда. Если окажется, что измеренный вектор скорости направлен в сторону Андромеды и его величина превышает относительную скорость сближения таких галактик, то, значит, Млечный путь гонится за Андромедой и собственная скорость Андромеды меньше скорости Млечного пути на величину скорости относительного сближения галактик.

Если окажется, что измеренный вектор скорости направлен в сторону, противоположную галактике Андромеда, то это означает, что Андромеда гонится за Млечным путем с большей скоростью. Зная величину и направление скорости перемещения галактики Млечный путь, а также скорость относительного сближения галактик, можно рассчитать столкнутся ли наши галактики через миллиарды лет. Вдруг, наша галактика летит куда-то плашмя, в даль туманную, и все-таки, уйдет от столкновения с Андромедой за миллиарды лет.

Нам все это безразлично, ибо в ту пору прекрасную жить не придется ни мне, ни тебе. А, любителям сочинять страшилки, такое знание пригодится.

10.2. Доказательство абсурдности в преобразованиях Лоренца

На рис. 9.1. мы видим, что вектор скорости годового перемещения Земли проецируется на вектор Vгс в виде синусоиды. Максимальное и минимальное значения величины такой синусоиды (амплитуды), мы не знаем, поскольку не знаем – каково взаимное расположение в пространстве вектора Vгс и плоскости, в которой расположена траектория годового перемещения Земли.

Амплитуда такой синусоиды может принимать значения, например, 30 км/сек. Такое максимальное значение амплитуды будет в том случае, если вектор Vгс лежит в плоскости годового перемещения Земли. При этом, если вектор скорости годового перемещения Земли совпадает по направлению с вектором Vгс, то такие вектора складываются и скорость Земли в мировом пространстве, относительно неподвижной сетки – возрастает. Если не совпадает, то – уменьшается.

Не будем забывать, что во всех наших рассуждениях, мы рассматриваем движение относительно неподвижной сетки. В случае, когда вектор Vгс не лежит в плоскости годового перемещения Земли, амплитуда синусоиды примет более низкое значение. Какое? Покажут измерения.

Синусный вид проекции вектора скорости годового перемещения Земли, на вектор Vгс, означает, что Земля, в зависимости от календарного срока на годовой временной шкале, перемещается в пространстве с различной скоростью. На рис. 9.1. точки максимального и минимального значений синусной амплитуды мы произвольно связали с некоторыми календарными датами. Например, пусть, максимальное значение такой синусоиды мы произвольно свяжем с 28 июня, а, минимальное значение – с 28 декабря. Реальная привязка к календарной шкале времени состоится при реальных измерениях векторов скорости.

Пусть, для определенности, минимальное значение такой синусоиды составляет – 15 км/сек, то есть, 28 июня Земля в пространстве летит со скоростью, на 15 км/сек меньшей, скорости Vгс. Пусть, максимальное значение такой синусоиды также равно – 15 км/сек, то есть 28 декабря скорость Земли превышает Vгс на 15 км/сек. Тогда, скорости перемещения Земли, измеренные 28 июня и 28 декабря будут отличаться на 30 км/сек. Это достаточно большая величина, чтобы проверить преобразования Лоренца.

Соберем в какое-нибудь место на поверхности Земли все виды часов, в том числе, и, цезиевые. Воспользовавшись математическими выражениями Лоренца, определим, как изменятся показания часов, при следующих данных: скорость галактики равна – 1000 км/сек; различия в скорости перемещения Земли, составляет – 30 км/сек. Если окажется, что реальные измерения времени совпадут с расчетными результатами, согласно преобразованиям Лоренца, то дружно споем оду восхищения преобразованиям Лоренца. И, наоборот, если показания часов (скорость хода часов) 28 июня, полностью совпадут с показаниями часов 28 декабря, то преобразования Лоренца можно будет положить на видное место в мусорное ведро. Туда же можно будет положить специальную теорию относительности. Поскольку, специальная теория относительности базируется на преобразованиях Лоренца.

Для убедительности, в таком эксперименте, можно привлечь абсолютного посредника – скорость света. Заставить свет пробегать заранее известное расстояние (например, один километр), по принципу туда и обратно (чтобы исключить влияние перемещения галактики). При этом, одними и теми же цезиевыми часами мы будем измерять время пробега светом такой двойной дистанции и 28 июня, и 28 декабря. Если ход времени в такие даты различен (согласно преобразованиям Лоренца он обязан быть различным), то преобразования Лоренца верны. Однако, мы уверены, что показания часов в такие даты будут одинаковыми, то есть цезиевые часы будут вырабатывать 9192631770 циклов колебаний излучения цезия в секунду, а, свет эти два километра (и 28 июня, и 28 декабря) пробежит одинаково в вакууме за 6670 наносекунд. Цезиевые часы при этом одинаково нащелкают 61364 цикла колебаний излучений цезия (и 28 июня, и 28 декабря).