
Полная версия:
Все науки. №8, 2024. Международный научный журнал
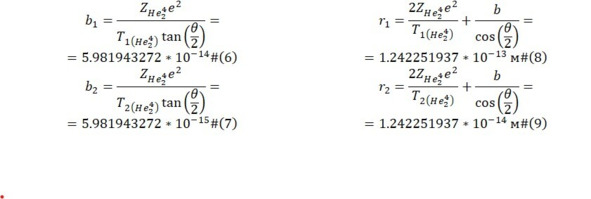
Результат наглядным образом демонстрирует достаточно большую по сравнению с радиусом действия ядерных сил 10—15 м величину, благодаря чему наглядно демонстрируется момент действия рассеяния Резерфорда. Возвращаясь к задаче о переводе значения дифференциального сечения рассеяния в процентное соотношение, для этого определяется материал мишени – кристаллический кремний с известной плотностью, массой ядра, а следовательно, и плотностью ядер (10), толщиной (11) и процентным соотношением (11—12).

Таким образом констатируется получаемый факт.
В результате, было определено, что из всего направленного пучка от 0,003106694% до 0,3101921% будут подвержены упругому рассеянию под воздействием рассеяния Резерфорда. Исходя из осуществлённых расчётов наглядно видно, что на момент действия системы космического излучения, имеющая в своей структуре заряженные частицы различной природы будет действовать эффект рассеяния Резерфорда, граничащий с системой ионизации.
Исходя из определений можно констатировать факт уменьшения процентного соотношения количества частиц, участвующие в настоящем явлении с ростом их энергии, что наглядно просматривается из типов частиц, участвующие в структуре пучков космического излучения. При том, что именно в структуре пучков космического излучения имеются высокоэнергетические частицы, констатируемые фактом, что также доказывает верность проведенных в ходе исследования расчётов.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Simon Knapen, and Steven Lowette. A Guide to Hunting Long-Lived Particles at the LHC. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023. Vol. 73:421—449 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-101920-013011
2. Roberto Franceschini. Physics Beyond the Standard Model Associated with the Top Quark. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023 Vol. 73:397—420 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-102020-011427
3. Brian D. Fields and Anton Wallner. Deep-Sea and Lunar Radioisotopes from Nearby Astrophysical Explosions. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023 Vol. 73:365—395 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-011823-045541
4. Zhen Cao, Songzhan Chen, Ruoyu Liu, and Ruizhi Yang. Ultra-High-Energy Gamma-Ray Astronomy. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023. Vol. 73:341—363 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-112822-025357
5. Aliyev I. X., Abdurakhmonov S. M. The algorithm of complex analysis of resonant nuclear reactions. Materials of the I International Scientific Conference «Modern problems of science, technology and production». SRI «PRNR». Electron Laboratory LLC. Ridero. pp. 193—217 p.
6. Aliev I. X. Aluminum resonant nuclear reaction. The international scientific journal «All Sciences». Electron Scientific School, Ridero. No. 3, 2022. 24—44 p.
7. Maria Lugaro, Marco Pignatari, René Reifarth, and Michael Wiescher. The s Process and Beyond. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023. Vol. 73:315—340 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-102422-080857
8. Marc Kamionkowski, and Adam G. Riess. The Hubble Tension and Early Dark Energy. ANNUAL REVIEW OF NUCLEAR AND PARTICLE SCIENCE Volume 73, 2023. Vol. 73:153—180 (Volume publication date September 2023) https://doi.org/10.1146/annurev-nucl-111422-024107
ИСПОЛЬЗОВАНИЕ СВОЙСТВА ИДЕАЛЬНОЙ ЖИДКОСТИ В МАЛОЙ ГИДРОЭНЕРГЕТИКЕ
UDK: 536.12
Ибратжон Хатамович Алиев, Султонали Мукарамович Абдурахмонов
Ферганский политехнический институт
Аннотация. Большие гидроэнергетические установки чаще всего используют изначальную конструкцию создания платины для увеличения напора входящей жидкости, что приводит к увеличению общего выхода энергии. В статье рассмотрено теоретическое предположение об использовании подобного метода увеличения скорости самого потока при помощи свойства идеальной жидкости из закона Бернулли и формулы Торричелли.
Ключевые слова: водный поток, напор, ускорение, скорость свободного падения.
Для больших гидроэнергетических установок часто преобладающими являются технологии создания плотин, где вода приводиться в близкое к статичному по отношению к общему объёму состоянию, после чего вода пропускается в канал, расположенный максимально низко под уровнем воды. Наличие такого ввода жидкости позволяет придавать массе дополнительную скорость благодаря потенциальной энергии, которая превращается в кинетическую.
Доказательством этого утверждения следует соотношение (1), из которого можно вывести как потенциальную энергию (2), так и кинетическую (3), далее при их равенстве (4), можно сделать вывод для скорости (5)

Но, чтобы указать на отношение этого вывода не только к обычным телам с высокой плотностью, то есть к твёрдым, но и к жидкостям, достаточно привести формулу Бернулли (6), вполне справедливую для жидкостей и вывод из неё этой же формулы (7—8).

Из этого видна возможность получения вторичного дополнительного вектора, который чаще всего преобладает и заставляет двигаться именно под давлением самой воды, а вектор скорости притока в само водохранилище чаще всего гасится. Но когда же дело обстоит с обычными малыми гидроэнергетическими установками, здесь ситуация обстоит по-другому, поскольку тормозная способность имеющегося малого объёма в «плотине» не так высока и определяется по коэффициенту трения воды о воду, если так можно выразиться. То есть каждый отрезок, уменьшение происходит именно на указанный коэффициент энергии (9).

Данный вектор скорости суммируется с образующимся вектором скорости из-за давления (8) под прямым углом образуя результирующий вектор (10).

Выводимый результирующий вектор логично будет больше изначального вектора скорости (11), благодаря чему можно сделать вывод того, что использование плотин в конструировании малых гидроэнергетических установок вполне целесообразная технология.
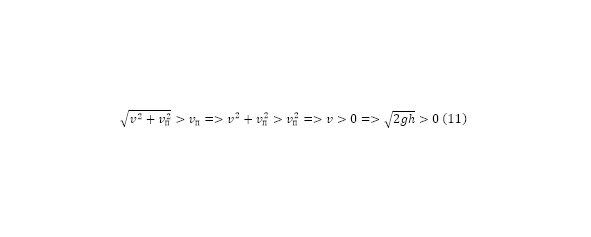
То есть какой бы ни была малой высота плотины и её разность между отверстием вывода потока и уровнем воды, действие, хоть и незначительное будет оказываться. Интересно здесь также и определение зависимости самой изначальной скорости и результирующего вектора (12).
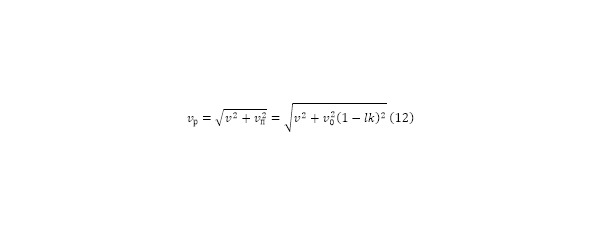
Эта зависимость была выведена, поскольку даже сама начальная скорость не совсем проста и за счёт того, что нижняя полость оврага для «водохранилища» должна быть выполнена в форме склона. Наряду с уменьшением по коэффициенту в зависимости от длины этого пути по (9), начальная скорость будет увеличиваться, поскольку к первоначальной скорости до входа в «водохранилище», при котором поток имел потенциальную энергию, кинетическая энергия, в которую превращается эта потенциальная, то есть действует тот же принцип (1—5), но при этом действует угловой коэффициент.
И если поскольку опять же этот потенциальный вектор направляющий вниз также находится под углом 90 градусов к основному первоначальному вектору, их суммированных вектор будет определяться по (13), создавая зависимость для начальной скорости от первоначальной в следующем расположении

И важно учесть, что (13) вместе с (14) действует только при плоском склоне самого оврага, не считая коэффициент трения, в случае его расчёта в (14) включается дополнительный коэффициент, ровно, как и в иных случаях, для реализации, но этот коэффициент определяется эмпирически.
При действии же (13) и (14), ранее описанная (12) изменяется как (15).
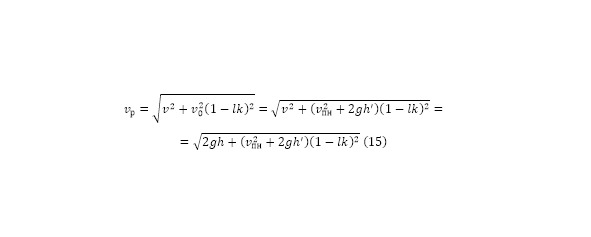
Таким образом (15) можно считать полноценной формулой при действии прямого склона на дне оврага. При наличии же нескольких векторов, целесообразно использование (16), по той простой причине, что несколько векторов не будут приходить из одного направления, ибо тогда их можно будет объединить в один. А разными вектора могут быть из-за наличия дополнительных поворотов, больших неровностей и подобных не существенных причин.

Заключительным штрихом служит лишь введение коэффициентов, о которых говорилось ранее, а именно о коэффициентах своего рода вязкости (18), зависящий от коэффициента сопротивления движения в потоке (17).
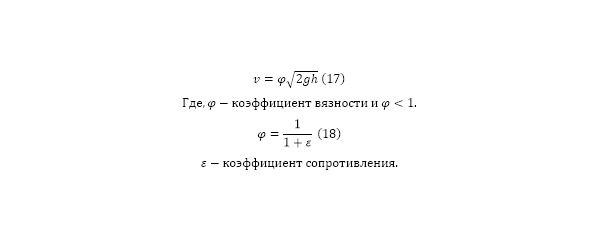
Такой вид (17) формулы (8) был доказан и описан итальянским учёным Эванджелиста Торричелли в 1643 году, а позже уже было показано, что эта формула, как уже упоминалось следствие закона Бернулли.
В заключении можно отметить, что развитие гидроэнергетики несёт в себе весьма прогрессирующий характер, что радует. И данное развитие требует всё новых и новых технологий, среди которых одним из лучших может стать технология использования «малого водохранилища» или искусственного рва с наклонным дном для увеличения эффективности всей гидроэнергетической установки.
Использованная литература
1. Evangelista Torricelli. De motu aquarium // Opera Geometrica. – 1644. C. 191. «Aquas violenter erumpentes in ipso eruptionis puncto eundem impetum habere, quem haberet grave aliquod, sive opsius aquae gutta una, si ex suprema eiusdem aquae superficie usque ad orificium eruptions naturaliter cecidisset».
2. Зиновьев В. А. Краткий технический справочник. Том 1. – М., Госиздат, 1949. – с. 362.
3. Савельев И. В. Курс общей физики. Том 1. Механика, молекулярная физика
О ТЕОРЕТИЧЕСКОМ ОПРЕДЕЛЕНИИ ЭНЕРГЕТИЧЕСКОГО ПОТЕНЦИАЛА ВЕТРА В СФЕРИЧЕСКИХ КООРДИНАТАХ ЗЕМЛИ
UDK: 531.51
Алиев Ибратжон Хатамович1, Абдурахмонов Султонали Мукарамович2
1НИИ «ФРЯР», ElectronLaboratoryLLC, 150100, Республика Узбекистан, Ферганская обл., г. Маргилан
2Ферганский политехнический институт, 151100, Республика Узбекистан, Ферганская обл., г. Фергана
Аннотация. В работе рассмотрена теоретическая модель образования ветра в сферических координатах Земли с учётом расчёта образуемых мощностей и скоростей ветра. Для моделирования использованы функции в сферической системе координат по определению точек выбора расчёта и величины смещения. Расчёт проводился на основе данных плотности атмосферы, расчётной точки и высоты размещения ветряных генераторов. На основе полученной модели построены графики расчётно-образуемых мощностей и скоростей ветра по Земляным координатам. Указываются совпадения теоретических результатов с экспериментальными данными.
Ключевые слова: сферические координаты, земляные координаты, образуемая мощность, периодичность, направленность.
Введение. В настоящее время на Земле истощаются традиционные источники энергии нефть, газ и уголь, поэтому основным направлением научных и инженерных исследований направлено на поиск альтернативных, возобновляемых источников энергии [1—2; 4]. Одним из них является ветряная энергетика. Для получения энергии ветра разработаны и сконструированы различные установки. Эффективность этих установок в настоящее время достигло до 40% от энергии ветра. Построение ветряных энергетических установок требует учёт возможностей существующих энергетических потенциалов атмосферы [2; 3—5].
Энергия ветра измеряется с использованием энергетического метрологического оборудования и на основе этих данных определяется траектория установки ветряных генераторов [6; 9—11]. В данное время не существует теоретическая модель, способная определить скорость и мощность ветра в координатах Земли. Теоретическое моделирование по земляным координатам скорости ветра дали бы возможность предварительного прогнозирования точек экспериментального измерения на земле. Кроме этого, в метрологических измерениях ветра наблюдается пико-образные данные скорости ветра, требующие теоретического объяснения возникновения. Поэтому проведение статистической и теоретической разработки модели формирования потоков ветра является актуальным.
Исследование. Для проектирования генерируемых мощностей, со стороны ветра, при учёте, что в системе будут использованы ветряные генераторы флюгерного типа, позволяющие изменять положение по направлению ветра, определяясь в стороны максимальной скорости ветра [7—8; 12]. Следовательно, устанавливается зависимость между скоростью ветра и генерируемой мощностью, где получаемая общая мощность равняется произведению кинетической энергии всего потока ветра и скорости ветра (1), с преобразованиями.
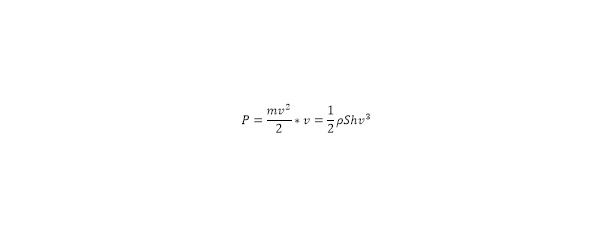
В выражении используется плотность атмосферы, высота получаемой энергетической точки и скорость ветра. В данном случае высота атмосферного слоя и плотность воздуха может приниматься за константу, площадь же может быть вычислена из запрашиваемых параметров, однако скорость ветра определяется исходя из температурной зависимости. Для этого следуя из условия постоянства объёма воздуха на планете Земля, система может рассматриваться в качестве изохорной, благодаря этому, действительно равенство по соотношениям:
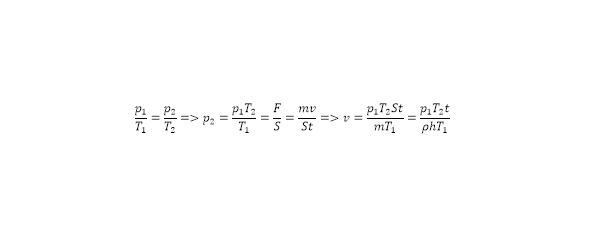
В данном случае первая величина давления равняется атмосферной, а температурные величины могут быть определены исходя из разности температур в двух задаваемых точках. Также вместе с этим появляется зависимость по времени.
Для вычисления температурного формирования используется закономерность неравномерной передачи энергии на планету со стороны Солнца [13] (3).

При использовании указанной функции зависимости от координат в сферической системе координат, а также по дополнительному времени начиная от даты зарождения Солнца, может быть получена величина температуры (4)
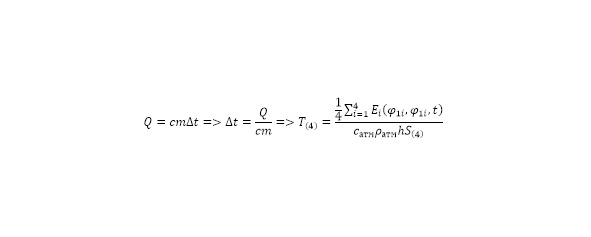
В формуле используется площадь криволинейного четырёхугольника на поверхности сферы, которая также учитывается в изначальных формулах. Исходя из всех преобразований, может быть сформирована единая форма для скорости ветра (5).
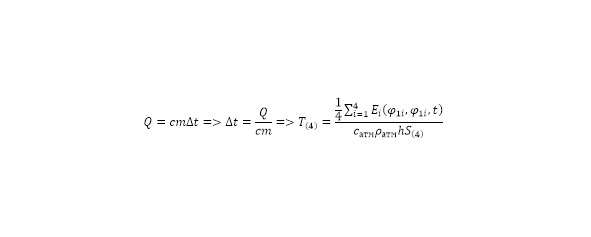
Для определения площади на поверхности сферы (O, R), необходимо следующее геометрическое моделирование. В формируемой задаче четырёхугольник ABCD имеет на поверхности сферы 4 точки с известными координатами широты, долготы и радиуса, формируя сферическую систему координат. При проекции с поверхности сферы на плоскость образуемого криволинейного четырёхугольника получается прямоугольник ABCD с четырьмя дугами —,, и в каждой из сторон.
Площадь сформированного прямоугольника SABCD вычисляется исходя из разности угловых координат. Так, при рассмотрении с точки зрения сечения и имеющихся координат всех 4 точек -, в силу равности радиусов могут быть преобразованы, как. Ещё одним аспектом рассмотрения с точки зрения сечения, является возможность определения длины отрезка между двумя координатами, при условии угла между двумя радиусами, соединённые дугой, между точками A и B, из свойства косинусов в треугольнике AOB (6).

Для вычисления площади дуг важно обратить внимание на то, что высота дуги прямоугольника на проекции равна высоте дуги на сечении, следовательно, вычисление сегмента окружности в проекции равна площади сегмента проекции прямоугольника на плоскость. Поскольку длина отрезка, на которую опираются линии радиусов, формирующие дугу известна в качестве стороны прямоугольника, для вычисления площади сегмента достаточно использование формулы площади сегмента (8).
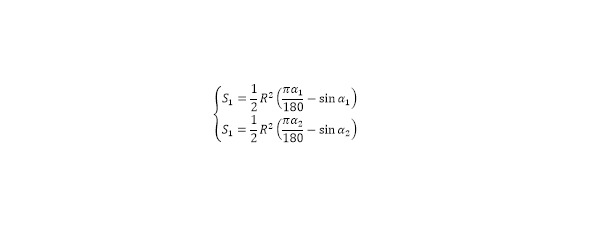
Исходя из этого общая формула площади составляет (9).
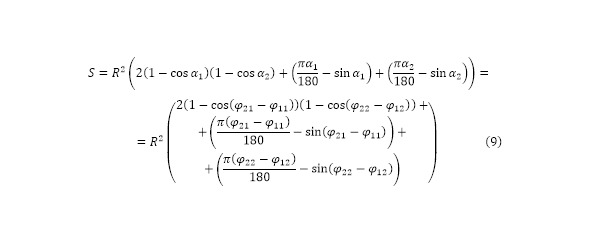
В результате подстановки полученных выражений площади в выражение скорости в (5), получается полная формула скорости (10).
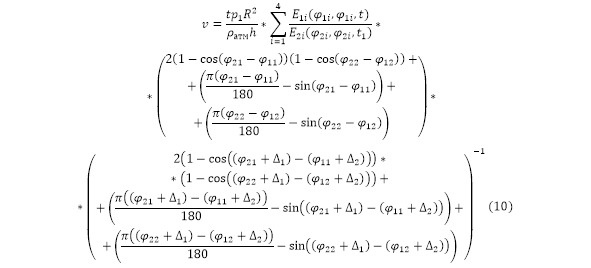
Последней стадией подстановки получается выведение значения выражения кинетической энергии, генерируемая посредством использования ветряных генераторов (11).

В результате была получена единая функция, зависимая от нескольких переменных, позволяющая моделировать значения образуемых мощностей ветра.
Расчёты. Для создания графика таковой функции необходимо использование несколько стадий ведения подсчёта. Величина детектируемых площадей на единицу дольной части остаётся константой, на основе чего определяется детектируемая площадь, при расчёте относительно всей планеты Земля равна 4 179,005 км2, формируя мнимый прямоугольник со стороной в 64,64522 км (эти данные определены исходя из минимальных возможностей расчёта). Следующей величиной являются значения функции энергии первой и второй стадии, отличающиеся разностью вводящихся значений углов при выбранном времени (Рис. 1—2).
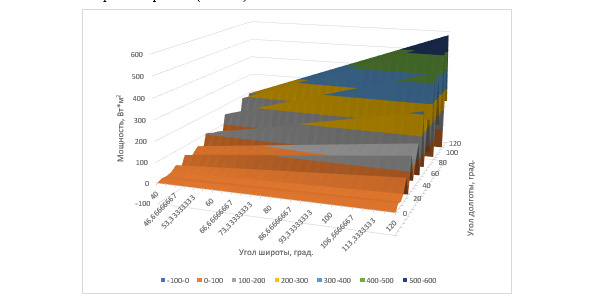
Рис. 1. График мощности в трёхмерных координатах в первой точке выбора
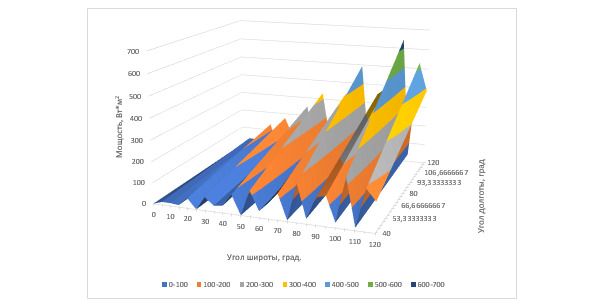
Рис. 2. График мощности в трёхмерных координатах во второй точке выбора
Полученные графики указывают на периодические полосы изменения мощности по Земляным координатам. Предполагается, что периодичность линий мощности связаны с изменениями дня и ночи в выбранных точках расчёта. На основе полученных данных по определению мощности, можно образовать график изменения скорости ветра по Земляным координатам для указанных точек расчёта (Рис. 3).
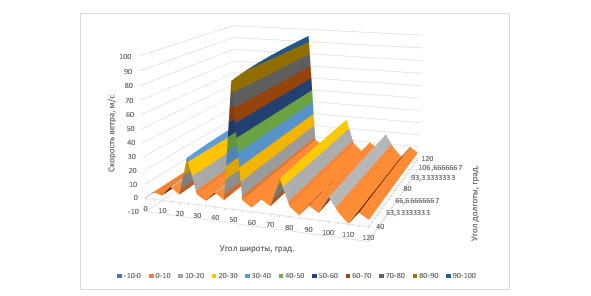
Рис. 3. График скорости ветра в трёхмерном пространстве
Полученные результаты теоретического расчёта коррелируются с реальным графиком скорости ветра (Рис. 4—5).
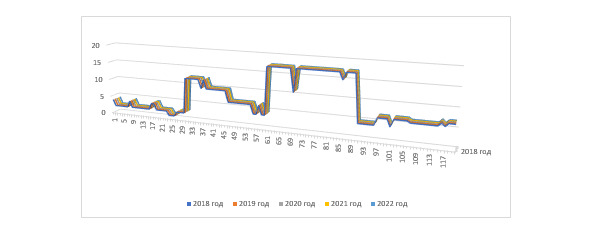
Рис. 4. Метрологические данные скорости ветра на протяжении 5 лет (2018—2022 гг.) [14—15]

Рис. 5. Усреднённый месячный график значений в промежутке 5 лет [14—15]
Представленные графики были получены метрологическим центром Ферганской долины посредством наблюдений на протяжении 5 лет, детектируя скорость ветра каждые 3 дня, при этом отмечая возможность масштабирования в планетарном масштабе, в силу использования фрактального подобия метрологических явлений.
Заключительной стадией моделирования является вывод графика функции образуемой мощности ветра (Рис. 6).
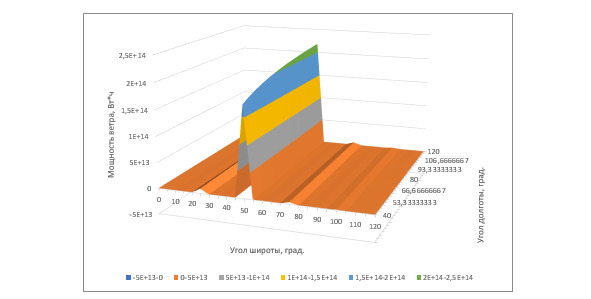
Рис. 6. Расчётная мощность ветра в трёхмерном пространстве
Заключение
Статистическое и теоретическое исследование показывает, что возникающая мощность ветра планеты зависит от Земляных координат, кроме этого, имеет периодичность. Периодичность изменения мощности может быть связана с наличием определённых каналов (направлений) возникающих потоков ветра на Земле. По проведённым расчётам максимальная пиковая скорость ветра наблюдается между основными океанами и возможно связано с особенностями рельефа Земли.
Использованная литература
1. Weather-sensitive renewable energy sources do not subject power systems to blackouts. Nat Energy 9, 1331—1332 (2024). https://doi.org/10.1038/s41560-024-01657-w
2. Parker, D.P., Johnston, S., Leonard, B. et al. Economic potential of wind and solar in American Indian communities. Nat Energy 9, 1360—1368 (2024). https://doi.org/10.1038/s41560-024-01617-4
3. Zhao, J., Li, F. & Zhang, Q. Impacts of renewable energy resources on the weather vulnerability of power systems. Nat Energy 9, 1407—1414 (2024). https://doi.org/10.1038/s41560-024-01652-1
4. de Kleijne, K., Huijbregts, M.A.J., Knobloch, F. et al. Author Correction: Worldwide greenhouse gas emissions of green hydrogen production and transport. Nat Energy 9, 1449 (2024). https://doi.org/10.1038/s41560-024-01644-1
Конец ознакомительного фрагмента.
Текст предоставлен ООО «Литрес».
Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Полная версия книги
Всего 10 форматов

