 Полная версия
Полная версияКак читать мир
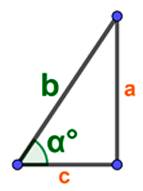
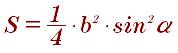
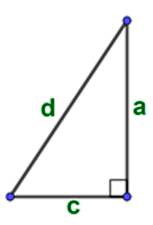
Площадь прямоугольного треугольника через катет и угол:
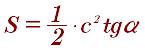
В случае, когда в прямоугольный треугольник вписан окружности она должна касается всех поверхностей и гипотенузы делит по полам для этого есть формула площади
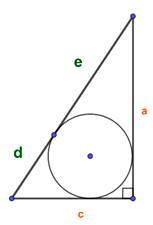
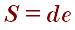
Вписав окружность в прямоугольной треугольник можно через гипотенузу найти площадь
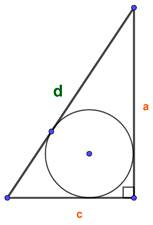
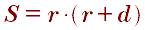
Для площади прямоугольного треугольника существует также формула Герона:
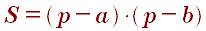
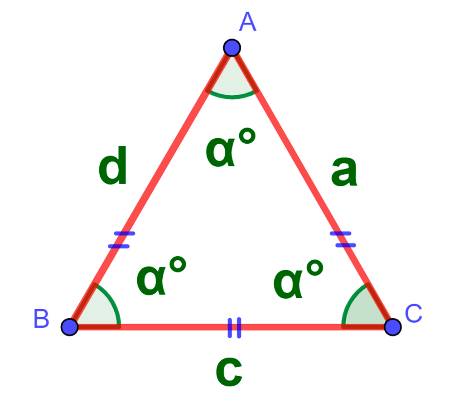
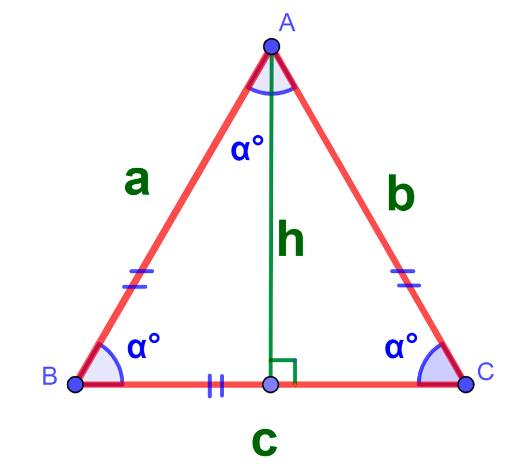
Равносторонний треугольник, у которого всё стороны равны. Формула площади по сторонам выглядит так:
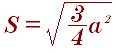
Площадь по высоте:
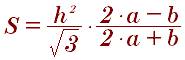
Площадь можно найти по радиусу вписанной окружности:
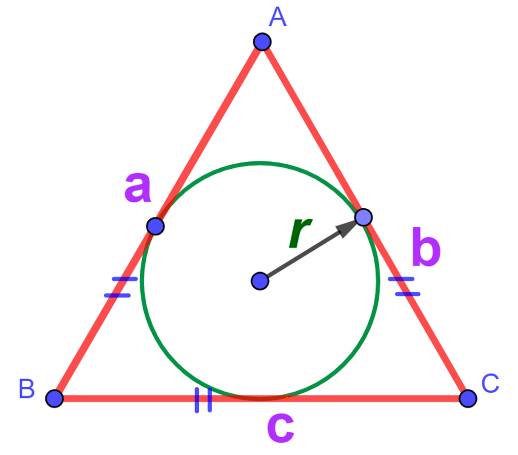
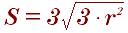
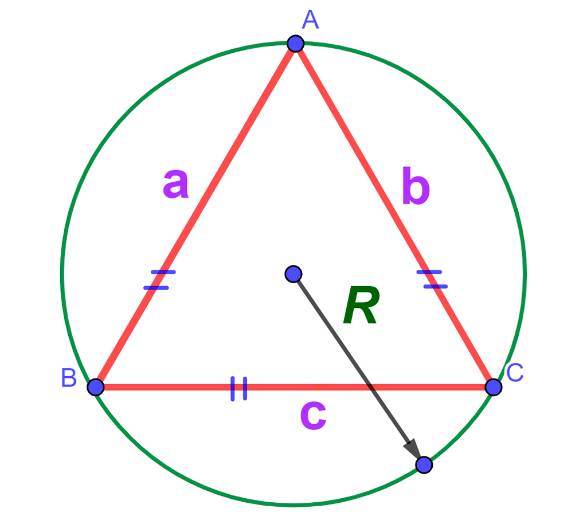
По радиусу описанного около треугольника окружности тоже можно найти площадь:
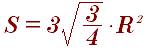
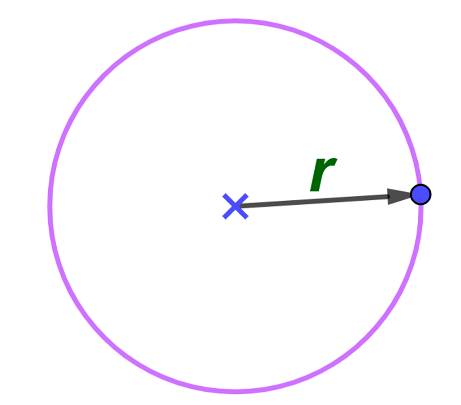
Круг самая фундаментальная фигура, которая очень часто встречается в природе площадь найти легко:
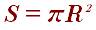
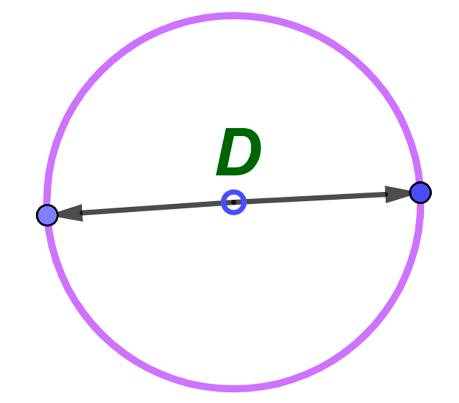
Площадь круга зная диаметр:
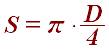
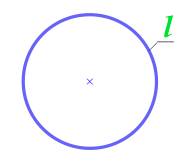
Площадь по длине окружности:
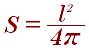
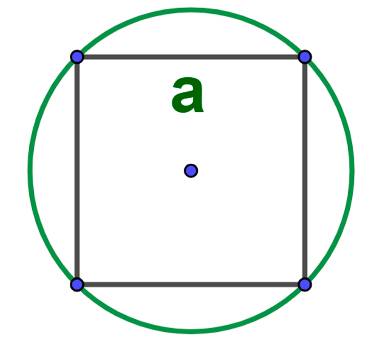
Чтоб найти площадь круга иногда помогают вписанные или описанные фигуры они следующие: через вписанный и описанный квадрат:
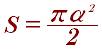
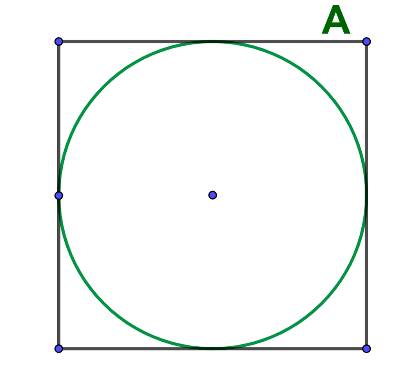
Формула площади вписанного в квадрат круга площадь находим по стороне А квадрата:
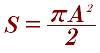
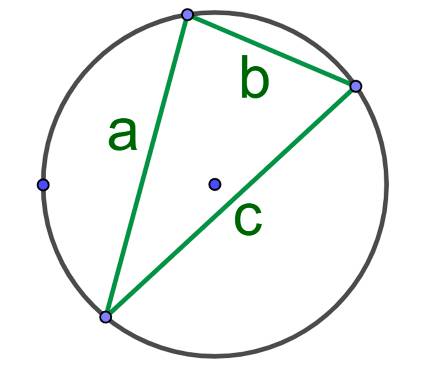
Площадь круга, описанного около произвольного треугольника:
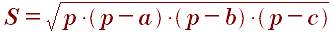
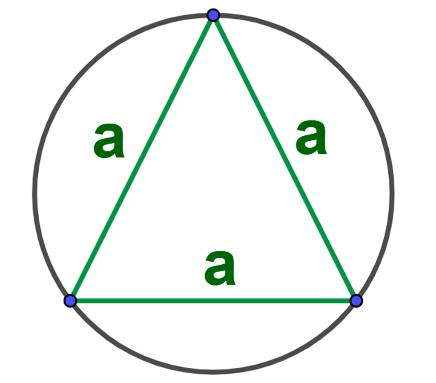
Описанный около равностороннего треугольника:
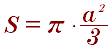
Площадь описанного круга зная высоту равностороннего треугольника:
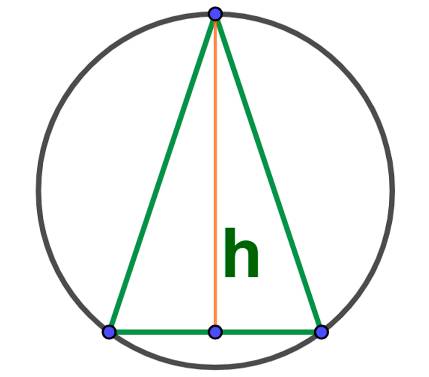
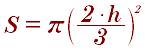
Площадь круга, описанного около равнобедренного треугольника:
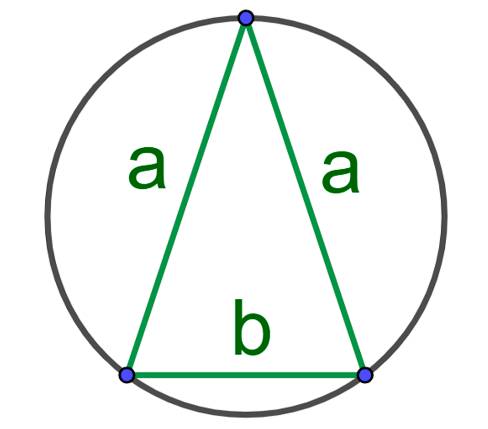
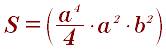
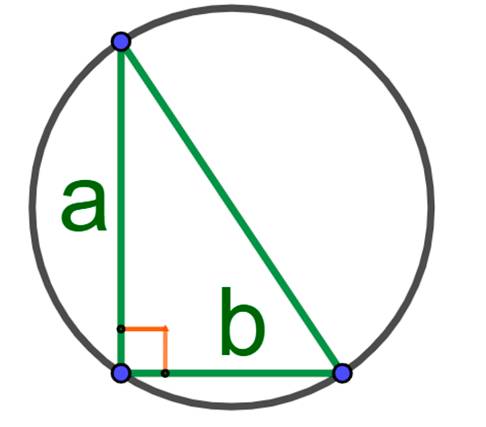
формула площади описанного круга около прямоугольного треугольника:
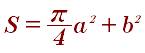
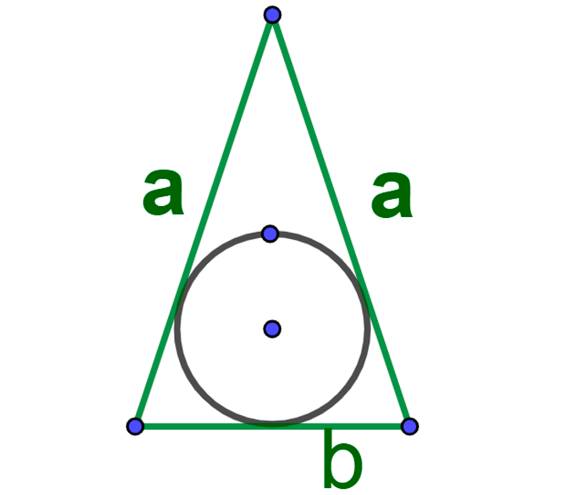
Формула площади вписанного круга в равнобедренный треугольник:

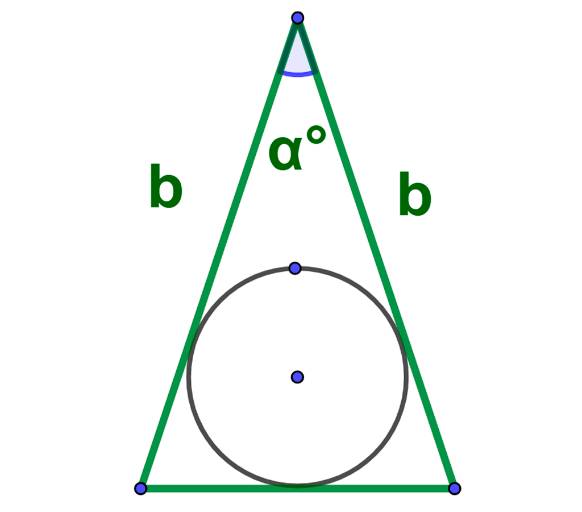
Формула площади вписанного круга в равнобедренный треугольник вычисляемый по боковым сторонам и углу между ними:
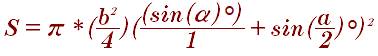
Формула вписанного круга в прямоугольный треугольник:
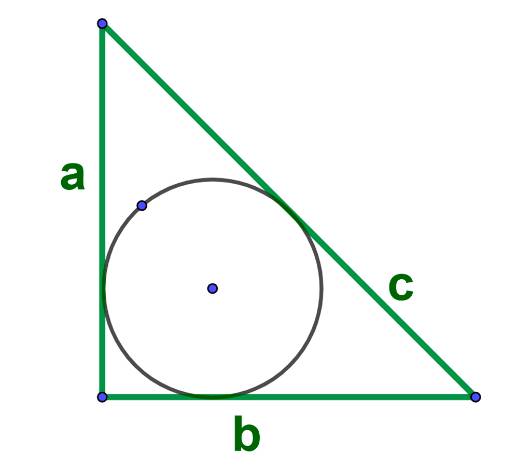
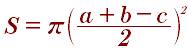
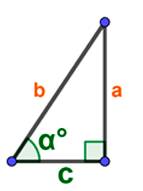
Вычисление площади по углу и стороне прямоугольного треугольника:
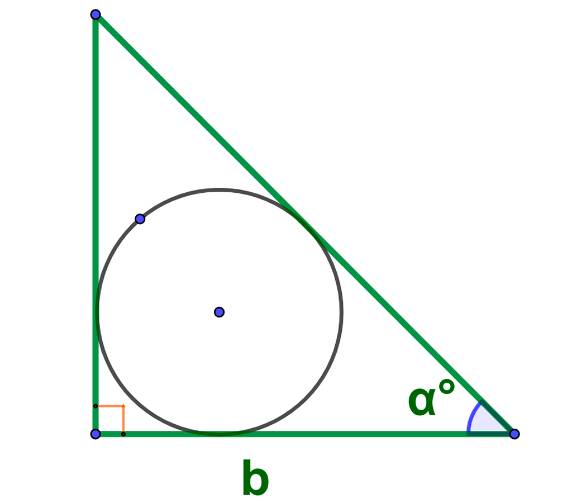
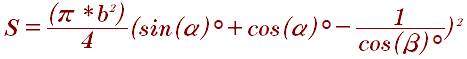
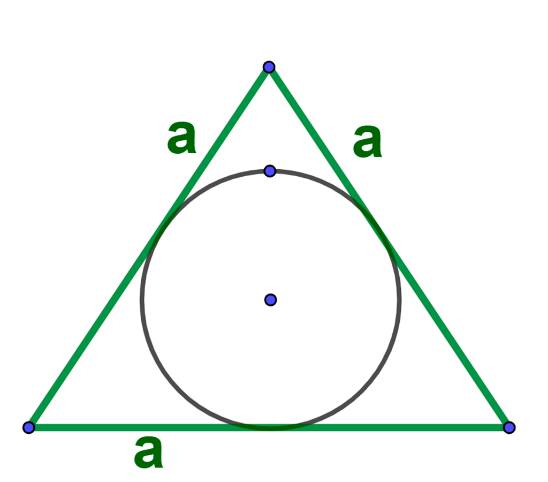
Площадь круга вписанный в равносторонний треугольник:
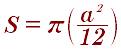
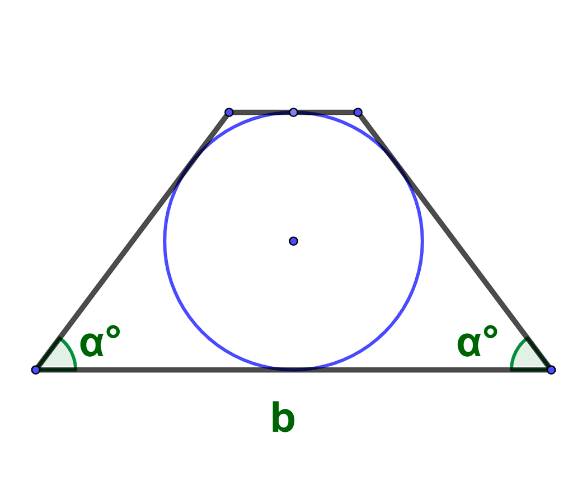
Площадь круга, вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании:
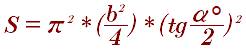
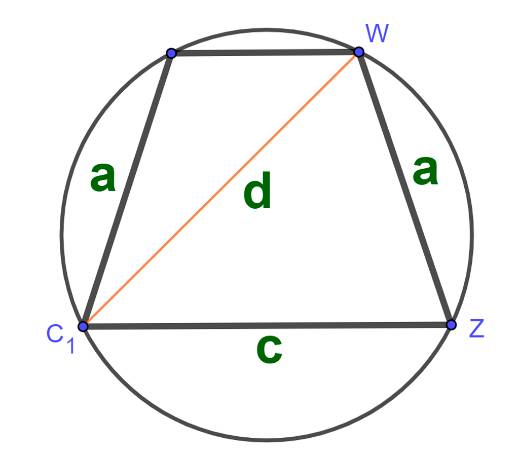
Чтобы рассчитать площадь круга, описанного около трапеции надо знать боковым сторонам трапеции, ее диагонали и основанию:
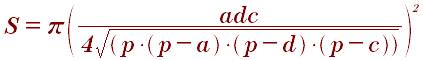
Площадь круга, описанного около прямоугольника:
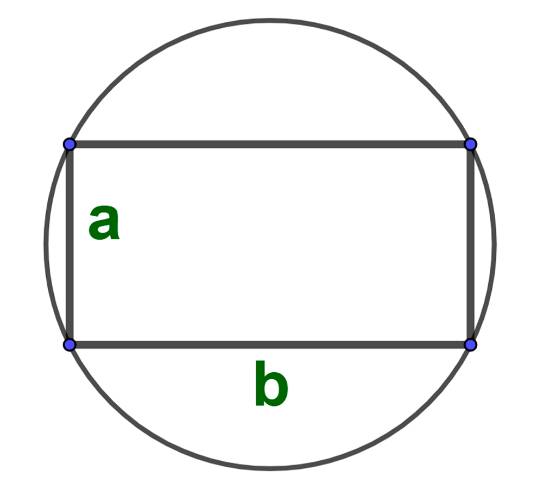
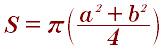
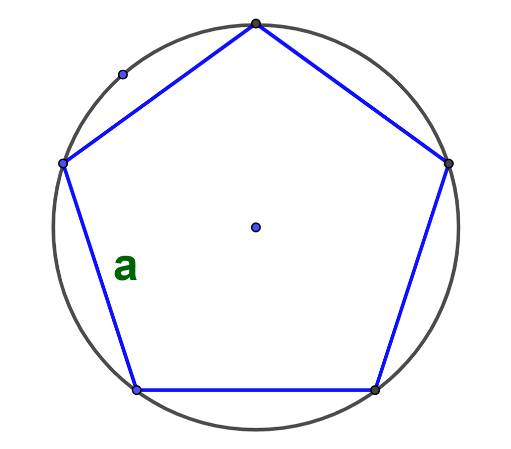
Формула для нахождения площади круга, описанного около правильного многоугольника:
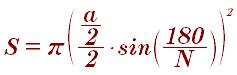
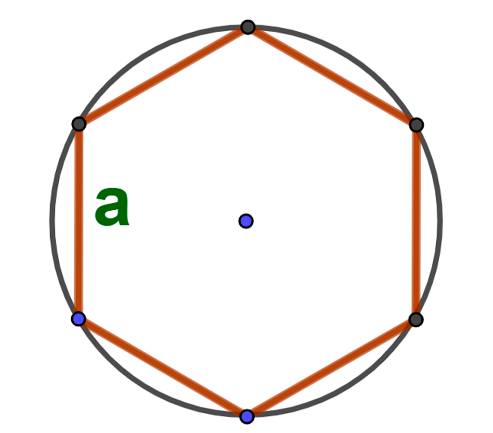
Площадь круга, описанного около правильного шестиугольника:
Приплюснутый круг с двух сторон называется Эллипсом.
Чтобы найти площадь данной фигуры надо узнать цени и построить отрезки под прямым углом к окружности формула следующая:
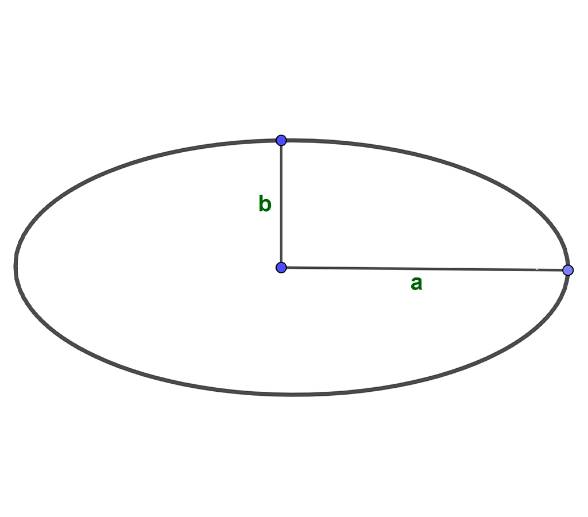
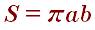
Формула для вычисления площади по осям следующая:

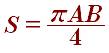
Площадь полу эллипса рассчитывается по следующей формуле:

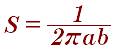
Площадь четверти эллипса рассчитывается так:

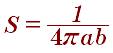
Трапеция не очень распространённая фигура, но знать формулы надо применятся в жизни очень часто.
Площадь по высоте и средней линии трапеции.
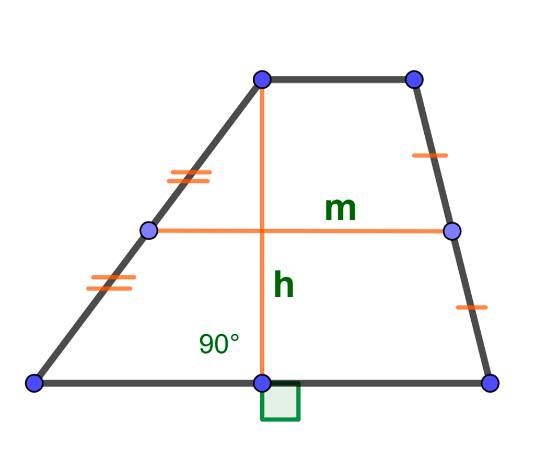
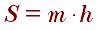
Площадь трапеции по четырем сторонам:

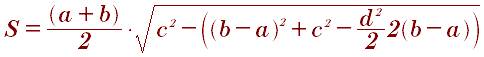
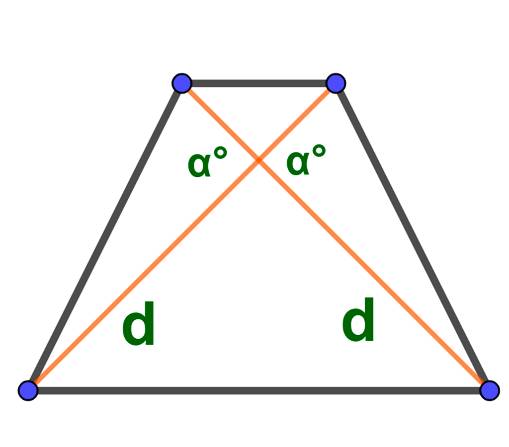
Площадь трапеции по диагонали и углу между диагоналями:

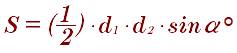
Формула площади где основным элементом являются углы возле основания:
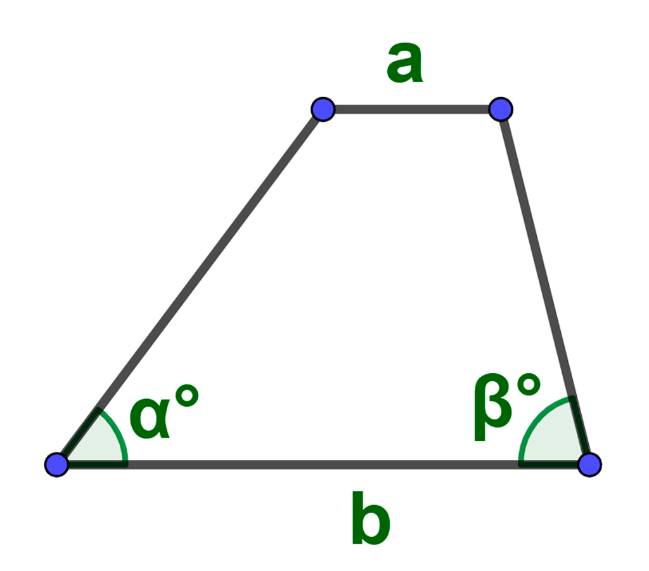
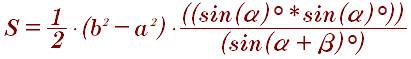
Площадь равнобедренной трапеции через ее стороны:
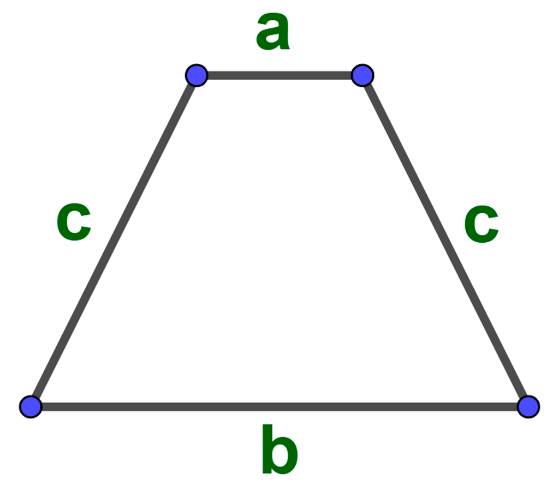
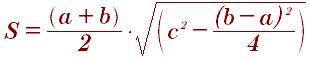
Формула для похождения площади через малое основание боковые стороны и углы возле большого основания:
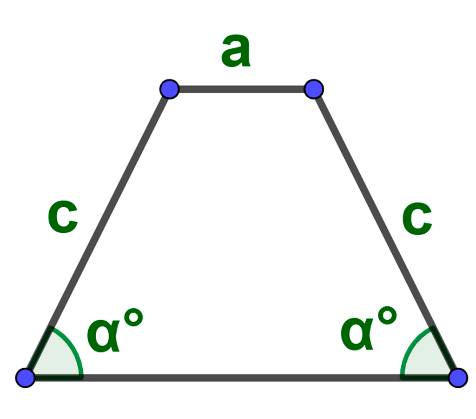
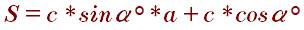
Площадь через большое основание боковые стороны и углы при большом основании:
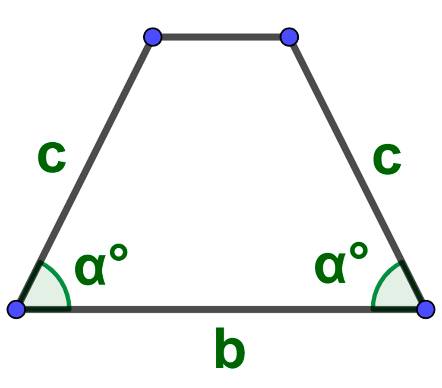
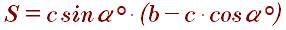
Площадь равнобедренной трапеции через основания и угол при основании:
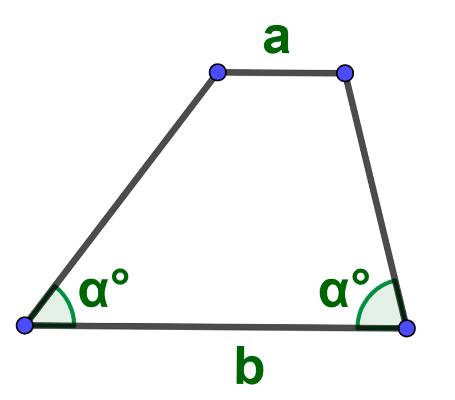
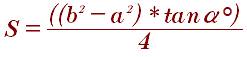
Формула где находят площадь через диагонали и углы между ними:
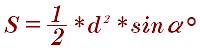
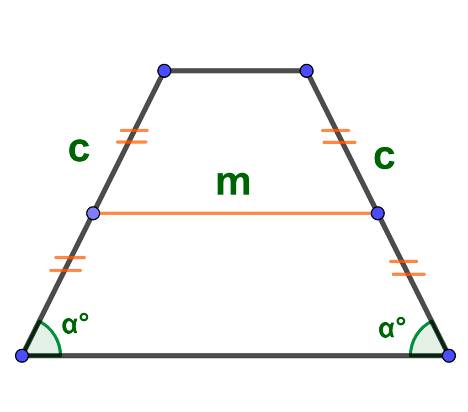
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
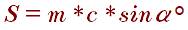
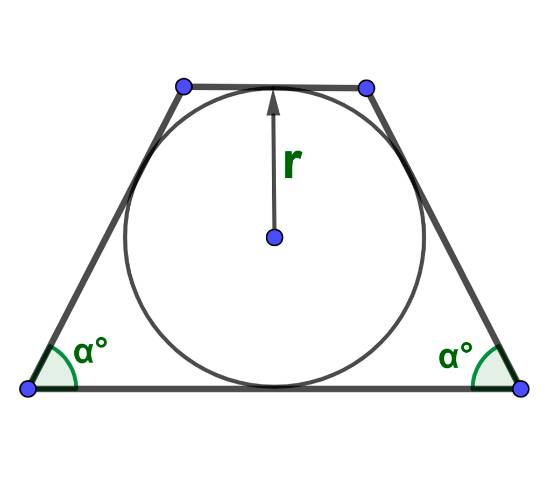
Площадь по радиусу вписанной окружности и углам между сторонами:
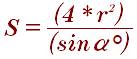
Площадь равнобедренной трапеции через два ее основания и радиус вписанной окружности:
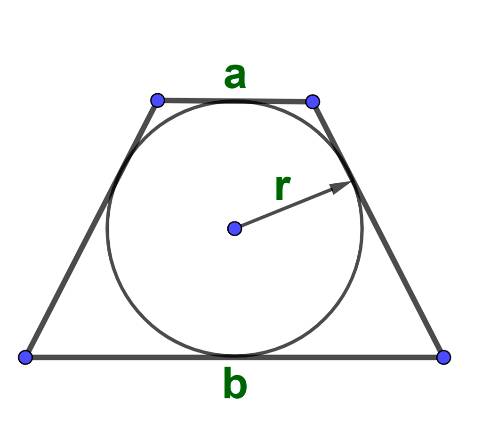

Площадь равнобедренной трапеции через ее основания и угол при большем основании;
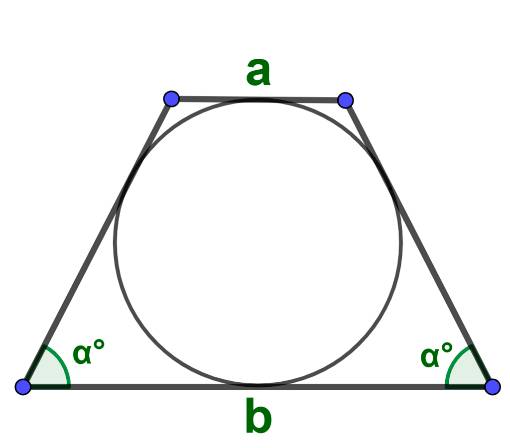
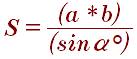
В трапеция которых можно вписать окружность через стороны площадь находится следующий образом:
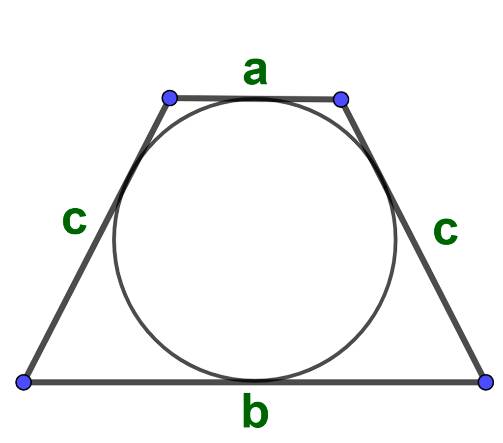

Площадь равнобедренной трапеции через основания и среднюю линию:
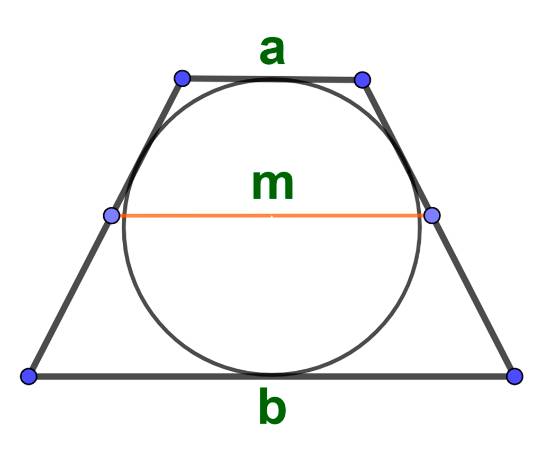
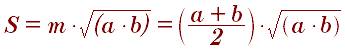
Площадь трапеции через основания и высоту:
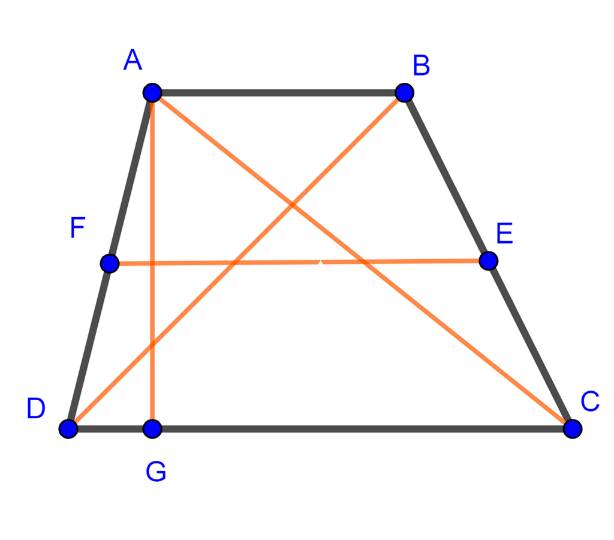
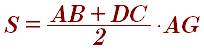
Зная все эти формулы можно читать площадь всех фигур во вселенной остальные частично или полностью образования от этих самых фигур.
Так чтоб определить самую простую площадь это площадь многогранников то вам понадобится разбить поверхность на определённые участки, например, на прямоугольные треугольники и площадь этой прямоугольного треугольника определённый вами с помощью формулы площади треугольника можно взять как единицу, а потом просто просуммировать это произведение на то количества треугольников, которое вышло у вас при разделении на треугольные сектора.
Если есть участки где сектор заканчивается на половине, то можно по формулы фигуры найти площадь, которая образуется в следствии и за размер ячеек и их неправильного расположения. можно также взять индивидуально данный участок и просчитать его чтоб получить общую площадь прибавив к основной площади.
для того чтобы находить ну очень трудные поверхности вам придётся брать экспериментальную технику все неровности измерить определить их площадь с помощью полигональной сетки и всё суммировать чтоб найти общую площадь.
Поверхности разные объединяясь пересекаясь по горизонтали и вертикали образуют объем. Следующая самая главная характеристика геометрии после периметра и площади.
мы все живём в трех мерном мире и видим мы проекции трех мерного мира в виде двух мерного. Трех мерность мира говорит о наличии трёх величин измерения верх вниз вперёд-назад влево право. Ученные строят разные теории на эту тему подробная разберём в другой главе.
так вот поверхности пересекающие и простирающиеся так что они входят в 3 мерный график образуют объем.
Квадрат формулу нахождения площади, которой мы уже разбирали становится объемным в том случае если добавить пять сторон пересекающихся и замкнуть все стороны со всех сторон.
Объем характеристика пространства, занимаемого телом или веществом.
Процесс в пустоте зависит от объема как от основного материального поля.
Объем в мире и для нас самая важная характеристика без объема мир в привычном понимании смотрелся не как надо. Объем измеряется системной единицей куб.
Измерение куба – это все стороны куба умноженные друг на друга у куба всё стороны равны и еда единица самая лёгкая в использовании. Можно даже найти объем прямоугольника просто складывая кубы по одному в месте. куб если что имеет сторону в 1м все три стороны образуют куб.
От одного метра уже происходят всё остальные 1см^3. Легчайший способ найти объем и точнейший если всё делать аккуратно особенно на практике, то это вытеснение воды из сосуда. Объем вытесненной воды равняется объему погруженного тела.
Но для определения объема тела теоретически применяют специальные формулы.
Объём прямоугольного параллелепипеда можно найти по формуле:
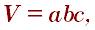
где a, b, c – его измерения.
Призма фигура, имеющая две основные напротив лежащие многоугольные плоскости и противоположные им плоскости, называемые сторонами призмы, которые также простираются против друг друга. эти боковые стороны параллелограммы называются гранями призмы, а многоугольные и напротив лежащие основаниями.
Для того чтоб найти объём призмы надо площадь основание умножить на высоту стороны.
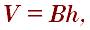
где – В это площадь основание призмы.
Пирамида многогранник, который имеет одну сторону основание, а другая заканчивается точкой одной общей для всех сторон призмы. формула нахождения следующая
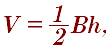
где – В площадь основания.
Мире часто встречаются усечённые фигуры, одним из которых является пирамида.

Четырёх гранёная призма всё стороны которой являются параллелограммами называется параллелепипедом:
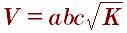
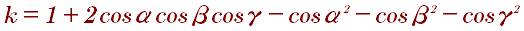
Многогранник, который состоит из четырёх треугольников называется тетраэдром. Довольно часто встречается в виде пирамид. пирамидой она является при принятии любой из сторон за основную. Тетраэдр образует 4 ребра и 4 вершин и 6 рёбер.
Тетраэдр, у которого все страны равностороннего треугольники называется правильным.

Формула для пирамиды с квадратным основание:
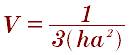
Шар объемное тело всё точки пространства которого находится от центра на заданном расстоянии от центра. Сфера – это поверхность шара. Замкнутый шар включает сферу, а не замкнутый исключает.
Объемлет шара вычисляется следующей формуле
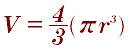
В мире часто встречается шар чем другие и у шара есть много видов формул такие как:
формула шарового сегмента
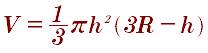
Формула шарового сектора:
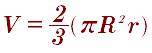
Формула шарового слоя:
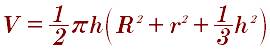
Сжимая шар в пространстве по 3 взаимно перпендикулярным осям, мы получаем эллипсоид.
Формула объект выглядит следующим образом:
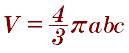
Тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями пересекающим её. Объем находится по следующей формуле:
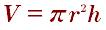
Конус фигура образования поверхностью, низ которой взят за круглую основу, а верх заканчивается одной точкой. Конус образована лучами и вершиной:
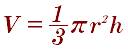
Также в мире существует усиленный конус, который встречается даже чаще и для него тоже есть формула:
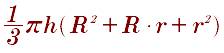
Для тех людей, которые скажут, что зачем нам знать объем разных геометрических фигур если мы хотим найти объем всего. так вот пишу для них формулы этих фигур, создают фундамент. зная формулы данных фигур можно найти любой объем ну если логически думать конечно, но тут я вам не помогу.
Чем труднее будет объект, тем больше времени и ресурсов придётся потратить. Сперва надо будет узнать характеристики сторон потом найти площадь простых составляющих объекта потом в силу вступает математика и умение решать уравнения и составлять уравнения по формулам мы и это разберём чуть по позже.
В мире много объектов разной фигуры, но нам может пригодится не их фигура, а то как они расположены в пространстве, когда решаем задачи на плоскости.
Плоскость – это бесконечная поверхность к которой прилегают всё прямые, которые могут пройти через данную точку.
Лучи которые пересекаются на прямой образуют угол отношения между ними a = (a, b).
Углы как геометрический объект разделяются на следующие виды. Углы всегда делят плоскость на две части внутреннюю и внешнюю.
Прямой угол образуется двумя лучами которые пересекаются перпендикулярно друг другу образуя радиан 90°.
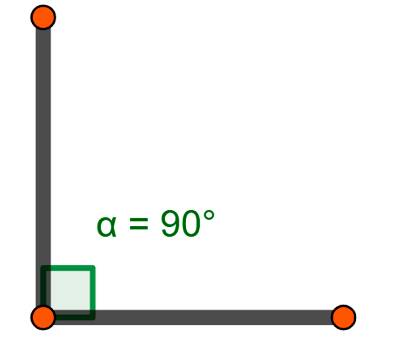
Развернув угол 90°, ещё на 90° получается полностью развёрнутый угол с градусом угла 180°.
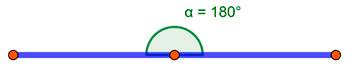
Если из центра развёрнутого угла провести прямую под 90°, то получается два сектора плоскости на которых делит этот луч:
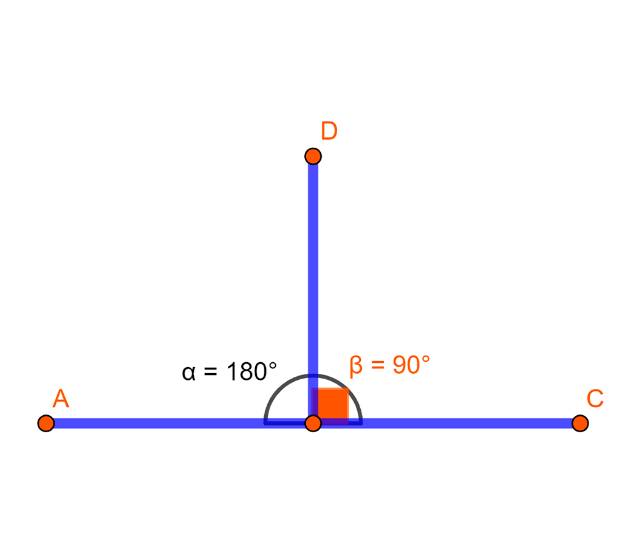
Если провести перпендикуляр в 1 секторе KPF, то получается угол острый, а если во втором KMF то угол тупой. в том случае если не считать смежный с ним угол:

