
Полная версия:
Фотонно-стимулированные технологические процессы микро- и нанотехнологии

А. М. Светличный, И. Л. Житяев
Фотонно-стимулированные технологические процессы микро- и нанотехнологии
Введение
В настоящее время фотонно-стимулированные технологические процессы на основе лазерных и некогерентных источников излучения прошли стадию лабораторных исследований и все шире используются в производственных процессах. Они стали одним из приоритетных направлений современного научно-технического прогресса. Это обусловлено широкими возможностями лазерных технологий, связанных с простотой управления, энергетическими и пространственными характеристиками лазерного излучения, возможностью осуществления локальности теплового воздействия и обработки материалов на воздухе или в специальных средах, отсутствием загрязнений, высокой производительностью и возможностью автоматизации процессов обработки [1-10].
За последние годы кроме традиционных появились новые области применения лазерного излучения для обработки материалов. Это лазерные технологии обработки порошковых материалов, лазерные технологии формирования покрытий, лазерная гальванотехника, технологии разделения хрупких неметаллических материалов путем формирования поверхностной трещины под действием лазерного луча, технологии быстрого прототипирования, т.е. создания сложных пространственных форм изделий с помощью лазерного излучения.
Особенно впечатляющие результаты получены в области бурно развивающейся в настоящее время лазерной технологии создания микроструктур больших интегральных схем (БИС), технологии создания сверхбольших интегральных схем (СБИС) в замкнутом объеме («in situ») методами лазерографии, лазерной технологии создания специализированных заказных и полузаказных СБИС, а также в новых областях развития современного приборостроения на основе микроэлектромеханических систем (МЭМС) и наноэлектроники.
На основе ксеноновых и галогенных ламп при длительных облучениях в секундном диапазоне градиент температуры по толщине пластины незначителен. Это не создаст предпосылок для образования термонапряжений в облучаемых структурах. В литературе эти процессы называют быстрой термической обработкой (БТО), скоростной обработкой (rapid thermal processing – RТР) и быстрым термическим отжигом (rapid thermal annealing – RTA). Важным преимуществом этих процессов является возможность тотальной обработки полупроводниковых пластин и микроструктур, низкое энергопотребление, невысокая стоимость оборудования и широкие функциональные возможности. Возможности этого метода значительно расширяются в технологии изготовления СБИС в случае использования комбинированных источников излучения: лазерных и некогерентных. Это позволяет целенаправленно управлять скоростью химических реакций в газовой среде и на поверхности обрабатываемых полупроводниковых структур. Например, ускоренное фотонно-стимулированное окисление всей поверхности пластин методами быстрой термообработки с использованием некогерентных источников излучения и последующее проведение локальных микрогетерогенных реакций осаждения, испарения, легирования, травления различных материалов с помощью лазерного излучения [4-7].
Развитие микроэлектроники с увеличением плотности элементов потребовало таких высокотемпературных технологических операций, которые бы не приводили к изменению профиля ионно-легированной примеси в активных областях СБИС. С увеличением быстродействия ИС необходимо было разработать технологические процессы, которые бы позволяли уменьшить глубину p–n-переходов, наносить ультратонкий подзатворный диэлектрик, изготавливать контакты к мелкозалегающим p–n-переходам. Это можно осуществить при адиабатическом режиме нагрева фотонным излучением полупроводниковых структур, при котором световой поток поглощается, и нагревается только приповерхностная область, а в объеме полупроводниковой пластины температура недостаточна для перераспределения примесей и изменения геометрии p–n-переходов. Этим требованиям полностью удовлетворяет лазерное излучение на длинах волн менее 400 нм при длительностях излучения 10-15-10-6 с. Высокая плотность светового потока, селективность воздействия лазерного излучения на обрабатываемые микроструктуры, импульсный характер, локальность и монохроматичность позволили его использовать на операциях отжига и рекристаллизации полупроводниковых слоев.
Полученные результаты позволили разработать технологические процессы лазерографии: локальное травление и осаждение микроструктур, легирование, создание контактно-металлизационной системы, программирование СБИС. Монохроматичность излучения позволила осуществить инициализацию химических реакций очистки, травления, осаждения материалов на поверхности полупроводниковой структуры. В основе этих реакций лежат не термические, а фотонно-стимулированные низкотемпературные процессы, связанные с резонансным воздействием на рабочую среду энергии излучения, достаточной для разрыва связей химических соединений. Это позволило воздействовать только на определенные типы молекул рабочей среды. Селективность воздействия лазерного излучения снизила на несколько сот градусов температуру технологических процессов без ухудшения электрофизических характеристик структур СБИС [3, 5, 8].
При использовании коротковолнового излучения энергии фотонов становится достаточной для возбуждения фотохимических реакций в газовой среде или на поверхности обрабатываемого материала. В результате температура технологических процессов может быть снижена до 300 °С и менее. Кроме того, на этих длинах волн преобладает приповерхностное поглощение светового потока. Это позволяет при уменьшении длительности импульса светового потока значительно уменьшить перераспределение примеси и повысить быстродействие полупроводниковых приборов и интегральных схем.
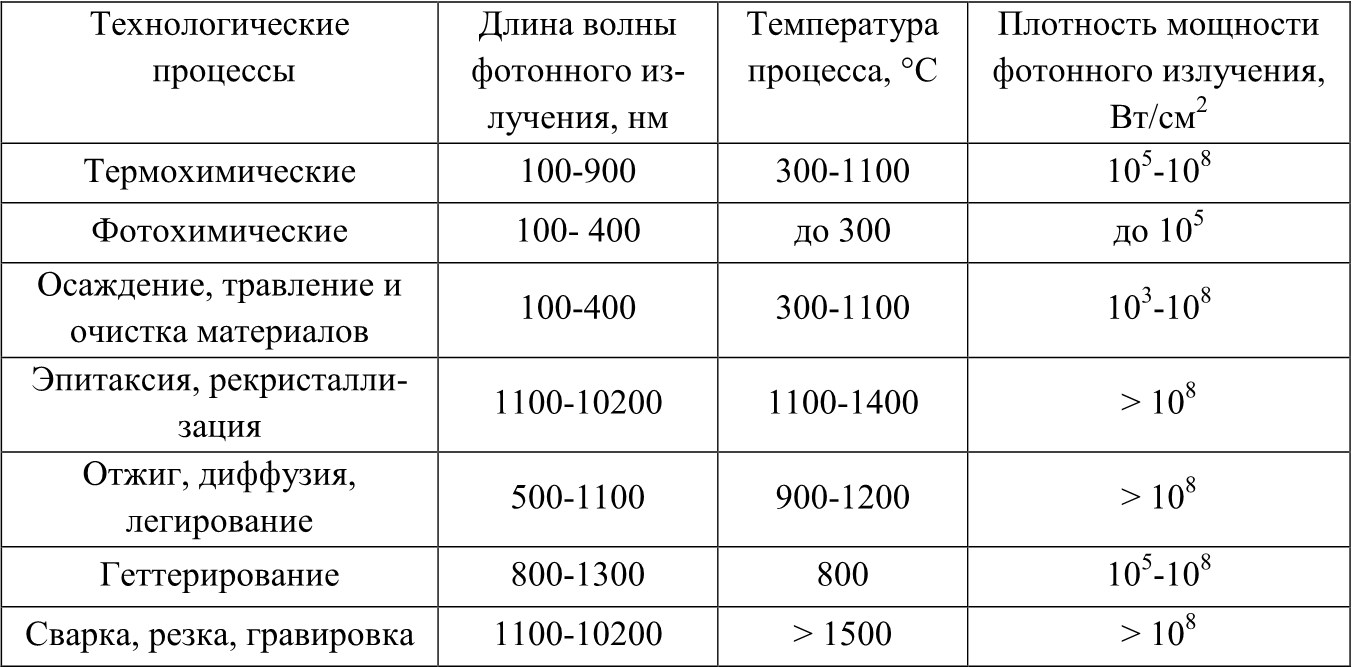
В табл. 1 показаны области применения и характеристики фотонного излучения, которые необходимы для осуществления различных технологических процессов. Как видно из табл. 1, для реализации фотонных технологических процессов в микроэлектронике используется широкий диапазон частот и мощностей лазерных и некогерентных источников излучений.
Таблица 1
Области применения фотонно-стимулированных технологических процессов в микро- и нанотехнологии
На рис. 1 приведены традиционные и фотонно-стимулированные технологические процессы, реализуемые с помощью лазерных и некогерентных источников излучения в производстве СБИС. Как видно из рисунка, возможности фотонных технологий значительно превышают возможности традиционных изотермических процессов. Некоторые из представленных процессов уже широко используются в технологии изготовления ИС. Некоторые, например геттерирование полупроводниковых структур на заключительных операциях изготовления ИС, получение графеновых пленок, изготовление автоэмиссионных структур, ещё находятся на стадии апробации и лабораторных исследований.
Анализ полученных результатов в области лазерных технологий показывает, что сдерживающим фактором при внедрении в промышленное производство применительно к микроэлектронике является недостаточная изученность физических процессов взаимодействия лазерного излучения с полупроводниковыми и пленочными структурами, отличающимися по своим оптическим и теплофизическим характеристикам. Кроме того, при лазерной обработке компонентов интегральных схем не всегда учитываются нелинейные параметры теплоемкости, теплопроводности, коэффициентов поглощения и отражения обрабатываемых структур, оказывающих существенное влияние на режимы обработки и воспроизводимость параметров технологического процесса. Сдерживающим фактором, несмотря на достигнутые успехи, является также недостаточный выбор источников лазерного излучения и отсутствие лазерного промышленного оборудования.
Успехи фотонных технологий были бы невозможны без достаточно развитой техники лазерного приборостроения и оборудования быстрой термической обработки полупроводниковых структур БИС, использующих некогерентные источники излучения.
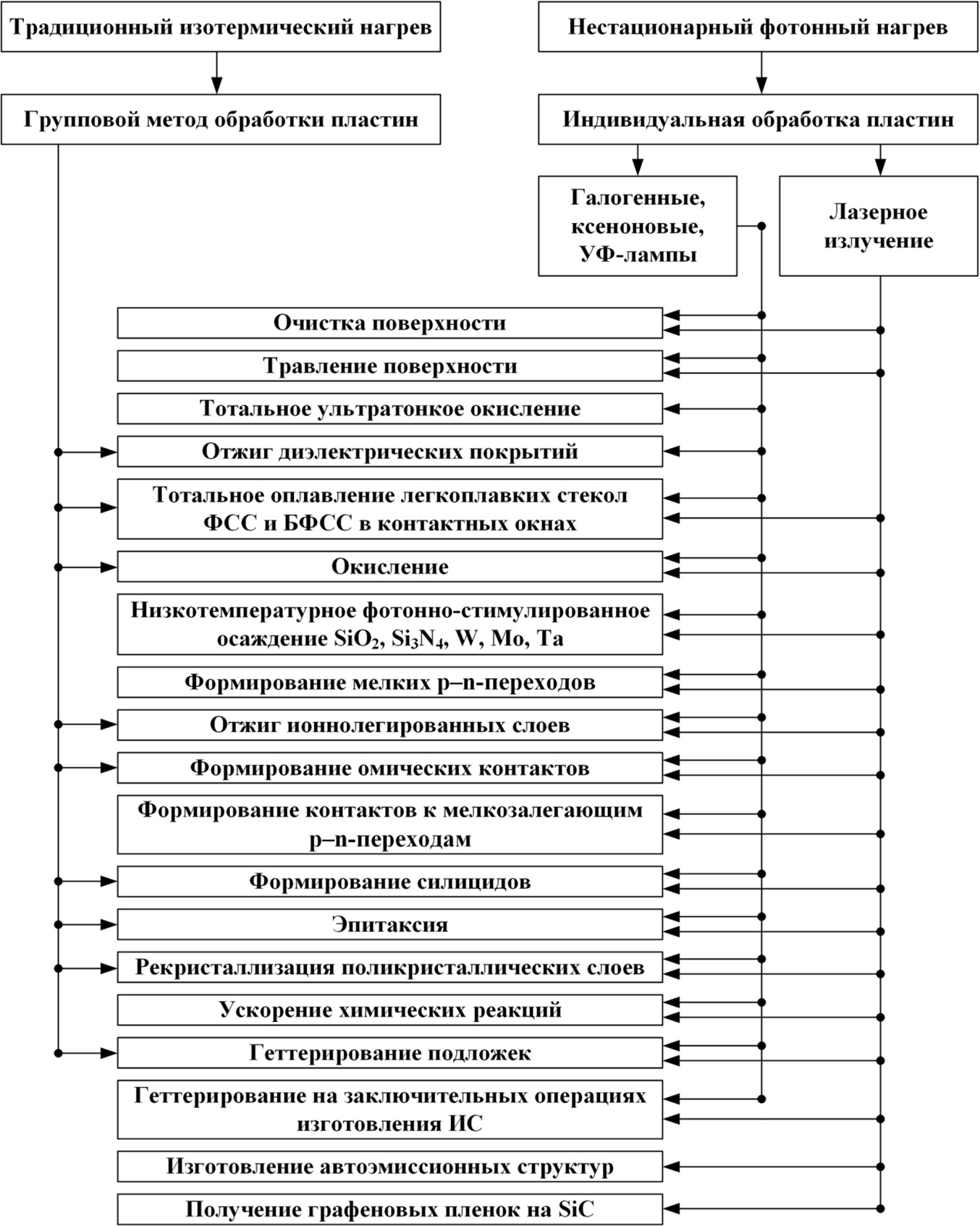
Рис. 1. Классификация традиционных и фотонно-стимулированных технологических процессов
1. Взаимодействие фотонного излучения с полупроводниковой поверхностью
1.1. Оптические свойства полупроводниковой структуры
Как известно, излучение, падающее на поверхность пластины, частично отражается, поглощается и может также пропускаться. Поэтому справедливо выражение для плотности потока излучения

где РR, PA, PT – части плотности мощности потока облучения отраженного, поглощенного и пройденного сквозь пластину соответственно.
Первое слагаемое в правой части определяется коэффициентом отражения RS, второе и третье – коэффициентом поглощения и толщиной пластины.
Проникновение излучения в глубину твёрдого тела описывается законом Бугера – Ламберта
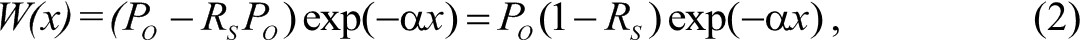
где α – коэффициент поглощения, x – координата по глубине. Тогда часть излучения, поглощенная пластиной толщиной dS, без учёта внутренних отражений будет равна
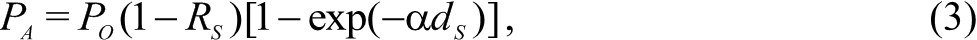
а выражение для плотности потока, прошедшего сквозь пластину, имеет вид

Уменьшение интенсивности фотонного излучения, проходящего через твёрдое тело, происходит за счёт взаимодействия с поглощающими центрами. Важнейшей оптической характеристикой облучаемой структуры является коэффициент поглощения.
В силу зависимости последнего от многих факторов (таких, как тип материала, концентрация легирующих примесей, дефектность структуры, температура, а также длина волны излучения) для адекватного моделирования рассматриваемых процессов необходим детальный анализ механизмов поглощения.
Полный коэффициент поглощения α равен сумме коэффициентов поглощения различными центрами:

В полупроводниках различают пять основных типов оптического поглощения:
– собственное;
– поглощение на свободных носителях;
– поглощение на локализованных состояниях;
– экситонное;
– решеточное [11, 12].
Световая волна, попадая в проводящую среду, воздействует на подвижные носители заряда. Электроны, ускоряясь, увеличивают свою энергию за счёт энергии волны. Сталкиваясь с решеткой, они отдают свою энергию решетке. Спектральная зависимость коэффициента поглощения свободными носителями заряда имеет вид

где е – заряд электрона; n, μ, mef – концентрация, подвижность и эффективная масса носителей заряда соответственно; с – скорость света в вакууме; ε0 – диэлектрическая постоянная;
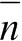
Если энергия фотонов больше ширины запрещённой зоны, то имеет место собственное поглощение, при котором электрон из валентной зоны может переходить в зону проводимости. При этом различают прямые и непрямые переходы электронов. В последних, характерных для кремния, наряду с фотоном и электроном участвует третья частица – фонон. Выражения для коэффициента собственного поглощения имеют вид
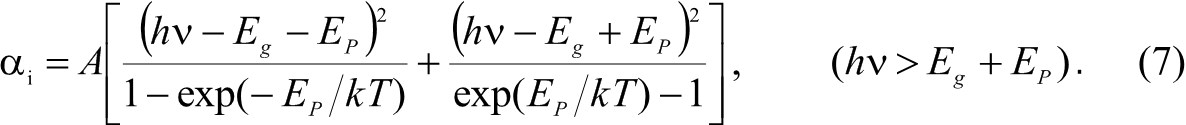
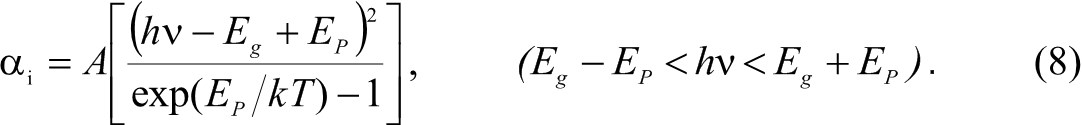

где hν – энергия фотона; Eg – ширина запрещенной зоны; EP – энергия фонона; А – константа [11, 13].
Фотон может также поглощаться электроном или дыркой, находящейся в локализованном состоянии. При этом заряженная частица переходит либо в свободное, либо в другое локализованное состояние.
Локализованные состояния могут иметь различную физическую природу: атомы примеси в узлах или междоузлиях, вакансии и др. Поэтому в общем случае достаточно трудно получить выражение для коэффициента поглощения данного вида. Однако если локализованные состояния имеют водородоподобный спектр, то к ним можно применить теорию излучения (поглощения) атома водорода.
Тогда выражение для коэффициента поглощения на локализованных состояниях можно записать как
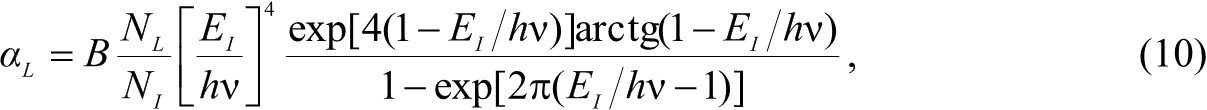
где NL, EI – концентрация и энергия ионизации рассеивающего центра; В – константа [11].
Входящие в (6-10) параметры Eg, n, μ сами являются функциями многих переменных. В частности, ширина запрещенной зоны Еg с ростом температуры и концентрации примеси уменьшается. Наибольшее влияние Eg на α проявляется в диапазоне температур 600-750 К из-за смещения края собственного поглощения в коротковолновую область.
Известная зависимость (11) для кремния не учитывает влияние дефектности и термохимических напряжений, однако они могут быть учтены с помощью коэффициента поглощения в локализованных состояниях [14].
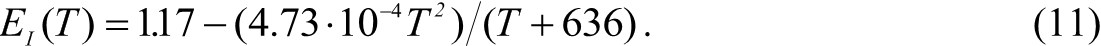
Концентрация свободных носителей заряда будет равна сумме собственной концентрации носителей ni, носителей, образованных ионизированными атомами примеси NI, и за счёт генерации неравновесных электронно-дырочных пар ng, поэтому справедливо будет выражение

Первое слагаемое в правой части определяется выражением [15]

Как видно, ni существенно зависит от температуры, что влечёт за собой высокую чувствительность α к температуре.
Концентрация ионизированных атомов примеси, определяемая коэффициентом активации, может изменяться в процессе лазерного нагрева, если происходит облучение ионно-легированных слоёв. Скорость же генерации неравновесных электронно-дырочных пар может быть найдена из выражения

где tp – длительность воздействия импульса излучения [16, 17].
Подвижность носителей заряда в кремнии определяется в основном рассеянием на акустических фононах и на ионизированных примесях и может быть выражена следующей зависимостью, например, для дырок [18]:
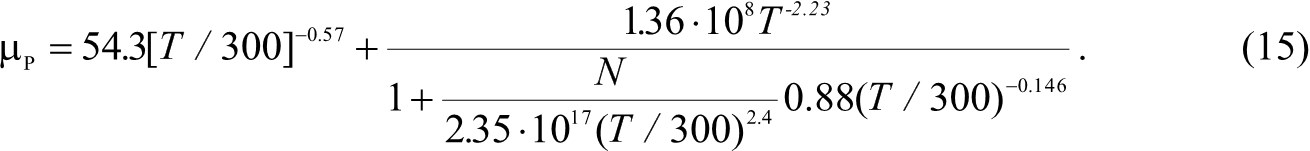
На рис. 2 показаны спектральные зависимости коэффициента поглощения для различных температур (а) и концентраций примеси в подложке (б). Видно, что в диапазоне температур использования лазерной обработки α изменяется на 4-5 порядков. Введение примеси также существенно увеличивает α. Совпадение расчётных и известных экспериментальных значений α свидетельствует о его удовлетворительной интерпретации в широком температурном и спектральном диапазонах.
Поглощение фотонного излучения плёнками металлов (например, Mo, Al) удовлетворительно описывается одной из составляющих коэффициента α – поглощением на свободных носителях (αfc), так как даже при низких температурах их концентрация велика.
Для диэлектрических слоёв коэффициент α определяется в основном собственным поглощением на локализованных состояниях, поэтому для этого случая может быть использовано выражение (12) при соответствующих подстановках входных параметров коэффициентов. Кроме того, при облучении слоистых структур имеют место интерференционные эффекты. В наибольшей степени они проявляются при использовании монохроматических источников излучения.
Второй важной оптической характеристикой облучаемой структуры является коэффициент отражения, также зависящий от многих параметров:
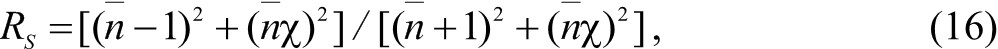
где
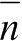
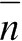
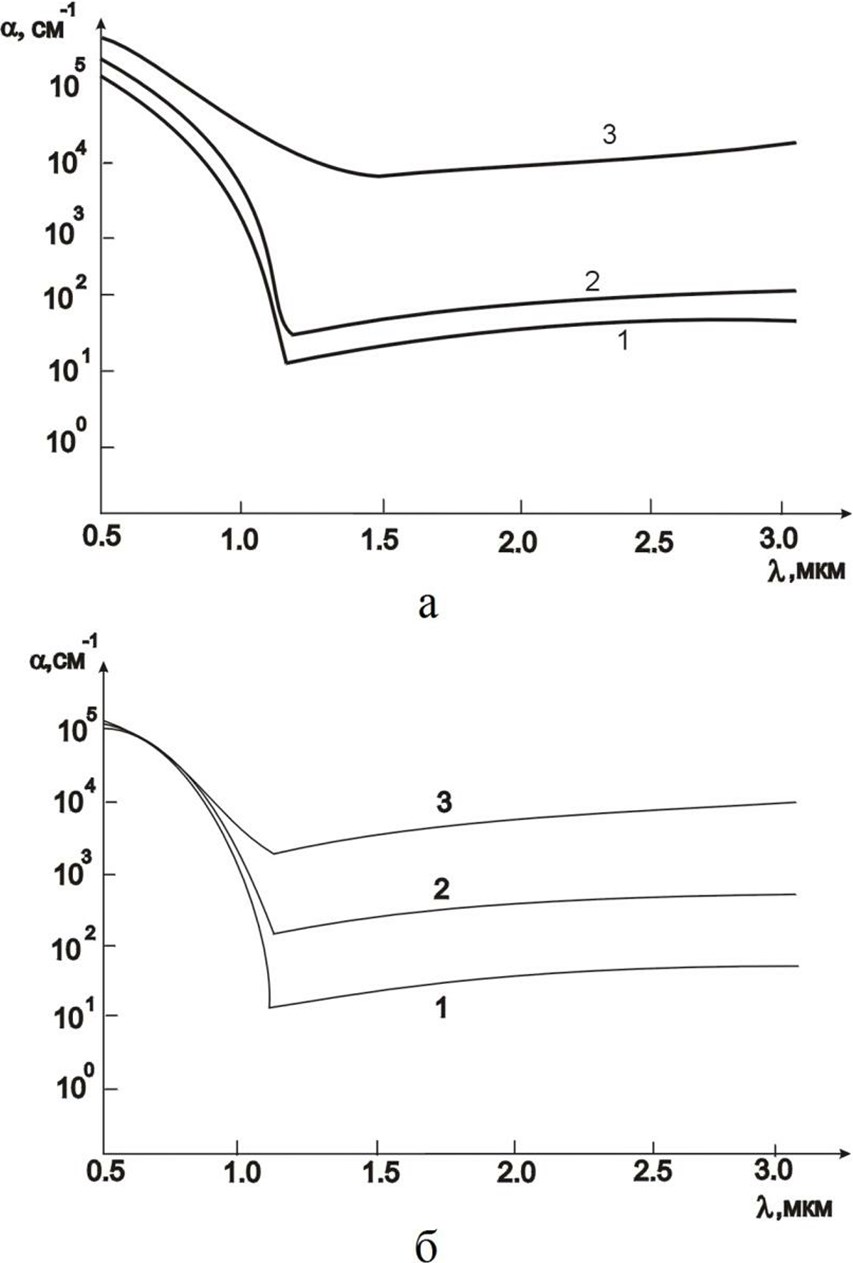
Рис. 2. Спектральная зависимость коэффициента поглощения кремния: а – при различной температуре отжига (1 – Т = 300 К; 2 – Т = 500 К; 3 – Т = 1000 К); б – при различной концентрации примеси (1 – Na = 1016 см-3; 2 – Na = 1017 см-3; 3 – Na = 1018 см-3)
Все рассмотренные выше зависимости характеризуют взаимодействие монохромного излучения с твёрдым телом.
1.2. Распределение температурных полей в кремниевой подложке при сканировании лазерным лучом
Рассмотрим полубесконечную подложку, по которой непрерывно со скоростью ν вдоль оси Х сканирует лазерный луч с эллиптической формой пятна площадью А и мощностью Р. Профиль распределения плотности потока мощности по пятну описывается кривой Гаусса (рис. 3)
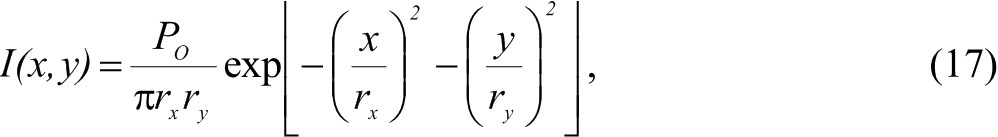
где rx ,ry – полуоси эллипса вдоль соответствующих направлений.
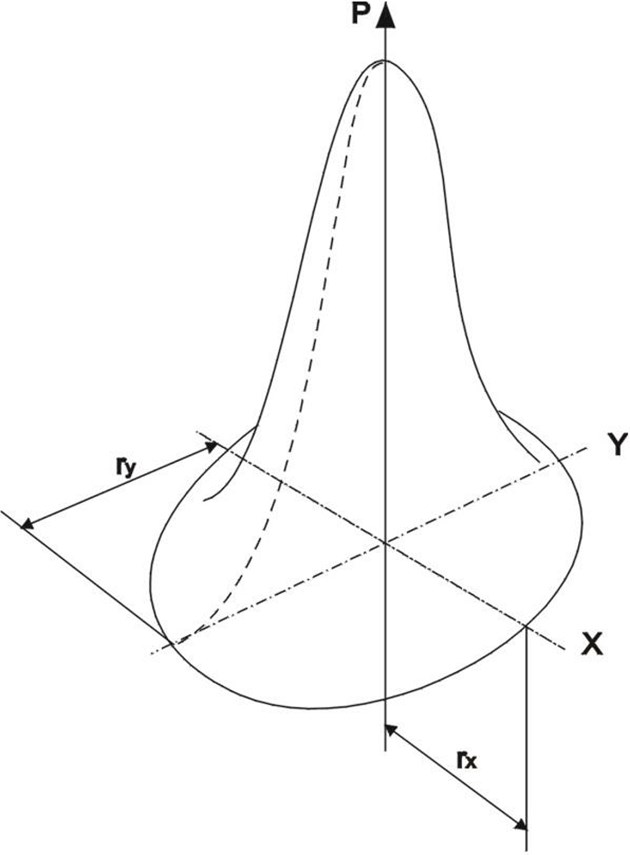
Рис. 3. Распределение интенсивности лазерного излучения по пятну эллиптической формы
Введём характеристический радиус r0 и параметр эксцентриситета β


Уравнение теплопроводности может быть записано как
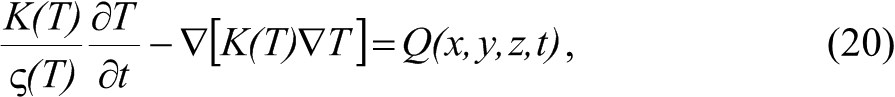
где первый член описывает изменение температуры Т во времени t, второй член описывает пространственное распределение Т, а третий является функцией теплового источника. Параметр К(Т) представляет собой коэффициент теплопроводности, зависящий от температуры, его размерность Вт/см·К.
Используя преобразование Кирхгофа
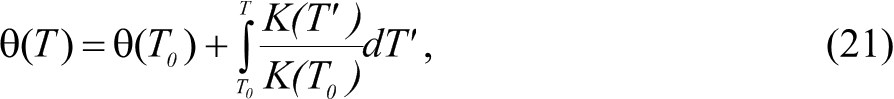
можно записать уравнение теплопроводности:
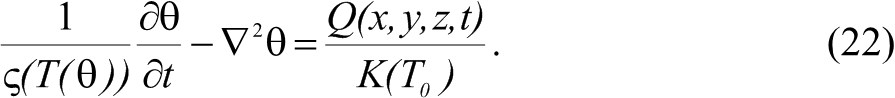
Для расчёта температуры в подложке при сканировании лазерного луча удобно использовать подвижные координаты: x’=x+νt. Однако далее будем использовать для удобства переменную х вместо х’, подразумевая её подвижной. В этом случае уравнение теплопроводности преобразуется к виду
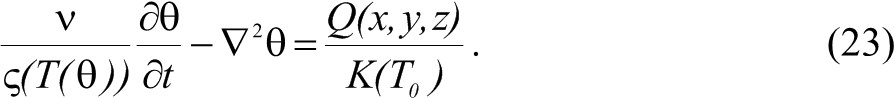
Считая, что лазерное излучение полностью поглощается в тонком приповерхностном слое, функция источника имеет вид
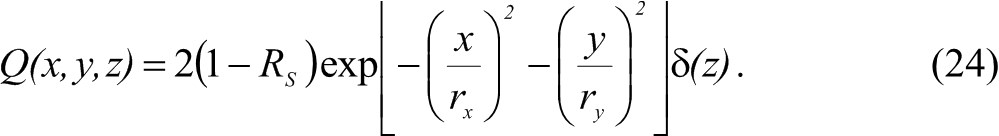
Множитель 2 показывает, что рассматривается полубесконечное пространство. Общее решение уравнения (23), полученное методом функции Грина, имеет вид где
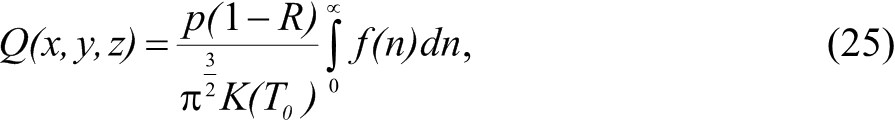
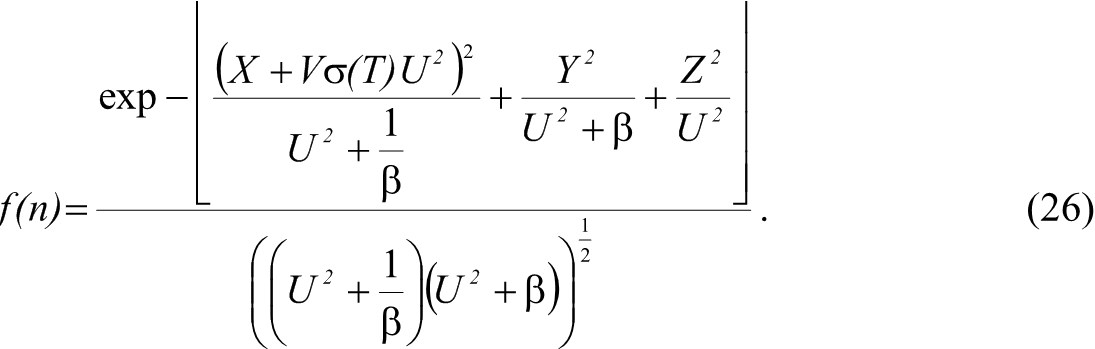
Координаты в этом выражении нормируются на характеристический радиус:
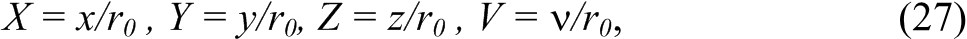


Зависимость T(θ) находится из преобразования Кирхгофа. Полученное соотношение является нелинейным, поэтому расчёт θ должен быть проведён итерационным методом. Однако при ν = 0 нелинейность исчезает, и температуру можно найти непосредственно прямым методом. При ν = 0 выражение (25) можно представить как произведение максимальной температуры (θ) в центре лазерного пятна на нормализованную функцию, определяющую вид температурного профиля по трём направлениям
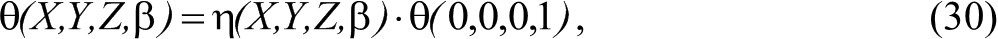
где
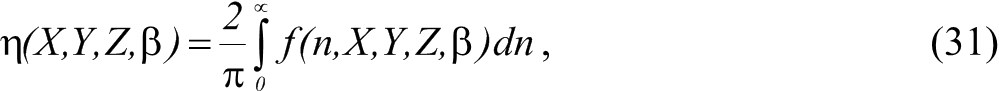

Профили η вдоль осей X, Y и Z, полученные по выражению (31) для подвижного луча, показаны на рис. 4 для β = 1. Расчёты показывают, что для луча диаметром 40 мкм распределение температуры до глубины 1 мкм, внутри которой формируются элементы ИС, практически однородно. Зависимости K(T) и ς(T) для кремния хорошо аппроксимируются выражениями [19]
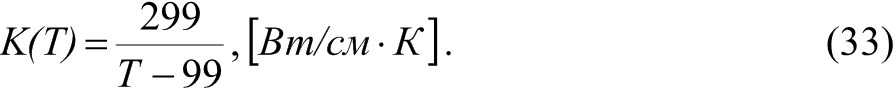

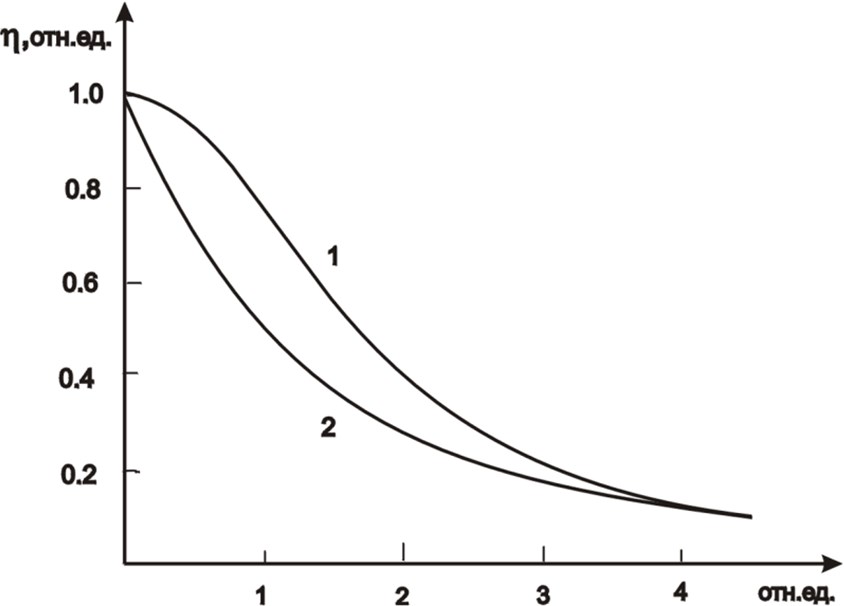
Рис. 4. Распределение относительной температуры вдоль нормированных координат при лазерном нагреве: 1 – Х, Y; 2 – Z
Это позволяет получить аналитическую зависимость
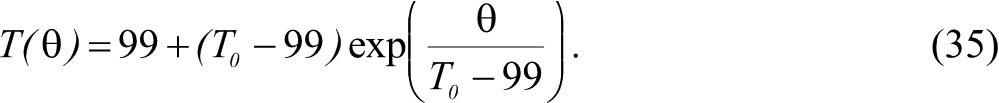
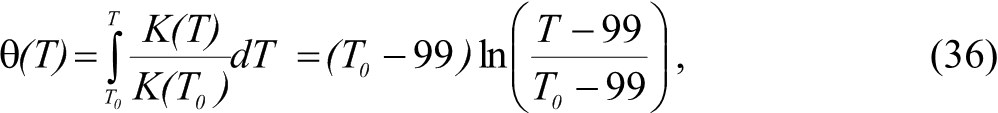
где Т0 – температура подложки до лазерного облучения.
Для неподвижного пятна Т может быть выражено через Р и Т0 следующим образом:
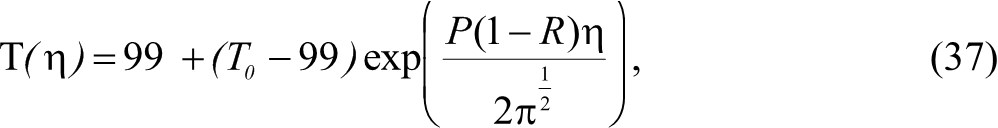
На рис. 5 показана зависимость максимальной температуры для неподвижного пятна при β = 1 как функция от Р. При скорости сканирования, отличной от нуля, θ зависит от параметров материала подложки, а также размеров пятна. Расчёт θ требует одновременного определения Т, поскольку θ = θ(σ(ς(T))) и T = T(θ).
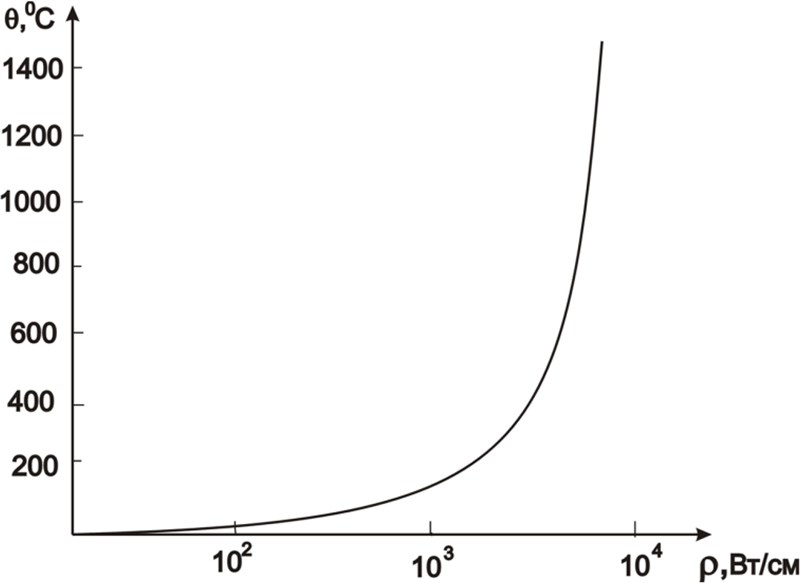
Рис. 5. Зависимость максимальной температуры в центре пятна от нормированной мощности лазерного излучения
«Истинная» температура (Т) может быть определена итерационным способом. На рис. 6 показаны температурные профили вдоль оси х при сканировании с различными скоростями.
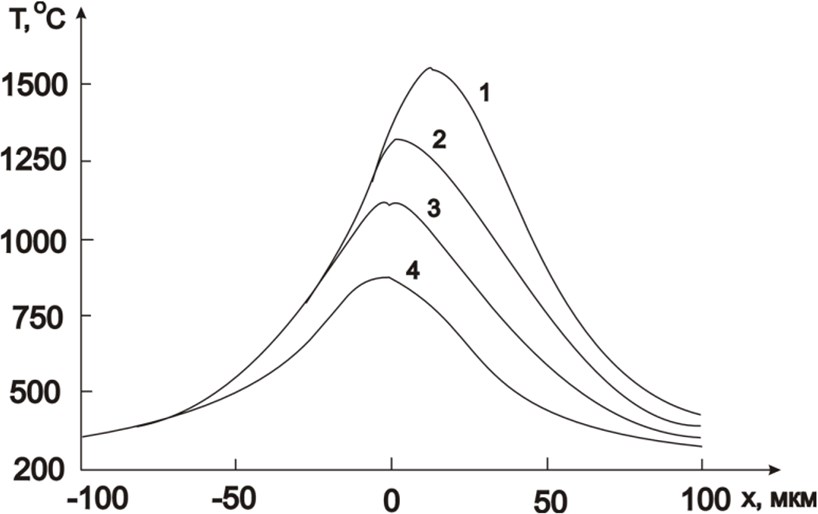
Рис. 6. Распределение температуры в кремниевой подложке вдоль направления сканирования луча с различной скоростью (Р = 4 Вт, r = 20 мкм, Тподл
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Полная версия книги
Всего 10 форматов



