скачать книгу бесплатно
Информатика и информационные технологии
Шпаргалки
Информативные ответы на все вопросы курса «Информатика и информационные технологии» в соответствии с Государственным образовательным стандартом.
А. В. Цветкова
Информатика и информационные технологии
1. Информатика. Информация
Представление и обработка / информации. Системы счисления
Информатика занимается формализованным представлением объектов и структур их взаимосвязей в различных областях науки, техники, производства. Для моделирования объектов и явлений используются различные формальные средства, например логические формулы, структуры данных, языки программирования и др.
В информатике такое фундаментальное понятие, как информация имеет различные значения:
1) формальное представление внешних форм информации;
2) абстрактное значение информации, ее внутреннее содержание, семантика;
3) отношение информации к реальному миру.
Но, как правило, под информацией понимают ее абстрактное значение – семантику. Если мы хотим обмениваться информацией, нам необходимы согласованные представления, чтобы не нарушалась правильность интерпретации. Для этого интерпретацию представления информации отождествляют с некоторыми математическими структурами. В этом случае обработка информации может быть выполнена строгими математическими методами.
Одно из математических описаний информации – это представление ее в виде функции
y = f(x,t)
где t – время,
x – точка некоторого поля, в которой измеряется значение y. В зависимости от параметров функции x и t информацию можно классифицировать.
Если параметры – скалярные величины, принимающие непрерывный ряд значений, то полученная таким образом информация называется непрерывной (или аналоговой). Если же параметрам придать некоторый шаг изменений, то информация называется дискретной. Дискретная информация считается универсальной.
Дискретную информацию обычно отождествляют с цифровой информацией, которая является частным случаем символьной информации алфавитного представления. Алфавит – конечный набор символов любой природы. Очень часто в информатике возникает ситуация, когда символы одного алфавита надо представить символами другого, т. е. провести операцию кодирования.
Как показала практика, наиболее простым алфавитом, позволяющим кодировать другие алфавиты, является двоичный, состоящий из двух символов, которые обозначаются, как правило, через 0 и 1. С помощью n символов двоичного алфавита можно закодировать 2n символов, а этого достаточно, чтобы закодировать любой алфавит.
Величина, которая может быть представлена символом двоичного алфавита, называется минимальной единицей информации или битом. Последовательность из 8 бит – байт. Алфавит, содержащий 256 различных 8-битных последовательностей, называется байтовым.
Под системой счисления подразумевается набор правил наименования и записи чисел. Различают позиционные и непозиционные системы счисления.
Система счисления называется позиционной, если значение цифры числа зависит от местоположения цифры в числе. В противном случае она называется непозиционной. Значение числа определяется по положению этих цифр в числе.
2. Представление чисел в ЭВМ. Формализованное понятие алгоритма
32-разрядные процессоры могут работать с оперативной памятью емкостью до 232-1, а адреса могут записываться в диапазоне 00000000 – FFFFFFFF. Однако в реальном режиме процессор работает с памятью до 220-1, а адреса попадают в диапазон 00000 – FFFFF. Байты памяти могут объединяться в поля как фиксированной, так и переменной длины. Словом называется поле фиксированной длины, состоящее из 2 байтов, двойным словом – поле из 4 байтов. Адреса полей бывают четные и нечетные, при этом для четных адресов операции выполняются быстрее.
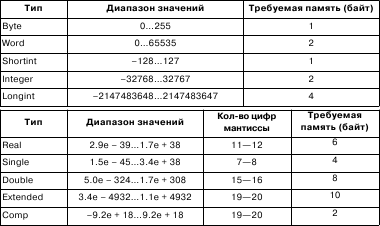
Числа с фиксированной точкой в ЭВМ представляются как целые двоичные числа, и занимаемый ими объем может составлять 1, 2 или 4 байта.
Целые двоичные числа представляются в дополнительном коде. Дополнительный код положительного числа равен самому числу, а дополнительный код отрицательного числа может быть получен по такой формуле:
x = 10n – \x\, где n – разрядность числа.
В двоичной системе счисления дополнительный код получается путем инверсии разрядов, т. е., заменой единиц нулями и наоборот, и прибавлением единицы к младшему разряду.
Количество битов мантиссы определяет точность представления чисел, количество битов машинного порядка определяет диапазон представления чисел с плавающей точкой.
Формализованное понятие алгоритма
Алгоритм может существовать только тогда, когда в то же самое время существует некоторый математический объект. Формализованное понятие алгоритма связано с понятием рекурсивных функций, нормальных алгоритмов Маркова, машин Тьюринга.
В математике функция называется однозначной, если для любого набора аргументов существует закон, по которому определяется единственное значение функции. В качестве такого закона может выступать алгоритм; в этом случае функция называется вычислимой.
Рекурсивные функции – это подкласс вычислимых функций, а алгоритмы, определяющие вычисления, называются сопутствующими алгоритмами рекурсивных функций. Сначала фиксируются базовые рекурсивные функции, для которых сопутствующий алгоритм тривиален, однозначен; затем вводятся три правила – операторы подстановки, рекурсии и минимизации, при помощи которых на основе базовых функций получаются более сложные рекурсивные функции.
Базовыми функциями и их сопутствующими алгоритмами могут выступать:
1) функция n независимых переменных, тождественно равная нулю. Тогда, если знаком функции является ?n, то независимо от количества аргументов значение функции следует положить равным нулю;
2) тождественная функция n независимых переменных вида ? ni. Тогда, если знаком функции является ? ni, то значением функции следует взять значение i-го аргумента, считая слева направо;
3) ?—функция одного независимого аргумента. Тогда, если знаком функции является ?, то значением функции следует взять значение, следующее за значением аргумента.
3. Введение в язык Pascal
Основные символы языка – буквы, цифры и специальные символы – составляют его алфавит. Язык Pascal включает следующий набор основных символов:
1) 26 латинских строчных и 26 латинских прописных букв:
2) _ (знак подчеркивания);
3) 10 цифр: 0 1 2 3 4 5 6 7 8 9;
4) знаки операций:
+ – О / = <> < > <= >= := @;
5) ограничители:. , ( ) [ ] (. .) { } (* *) .. : ;
6) спецификаторы: ^ # $;
7) служебные (зарезервированные) слова: ABSOLUTE, ASSEMBLER, AND, ARRAY, ASM, BEGIN, CASE, CONST, CONSTRUCTOR, DESTRUCTOR, DIV, DO, DOWNTO, ELSE, END, EXPORT, EXTERNAL, FAR, FILE, FOR, FORWARD, FUNCTION, GOTO, IF, IMPLEMENTATION, IN, INDEX, INHERITED, INLINE, INTERFACE, INTERRUPT, LABEL, LIBRARY, MOD, NAME, NIL, NEAR, NOT, OBJECT, OF, OR, PACKED, PRIVATE, PROCEDURE,
PROGRAM, PUBLIC, RECORD, REPEAT, RESIDENT, SET,
SHL, SHR, STRING, THEN, TO, TYPE, UNIT, UNTIL, USES,
VAR, VIRTUAL, WHILE, WITH, XOR.
Кроме перечисленных, в набор основных символов входит пробел.
В языке Pascal существует правило: тип явно задается в описании переменной или функции, которое предшествует их использованию. Концепция типа языка Pascal имеет следующие основные свойства:
1) любой тип данных определяет множество значений, к которому принадлежит константа, которые может принимать переменная или выражение либо вырабатывать операция или функция;
2) тип значения, задаваемого константой, переменной или выражением, можно определить по их виду или, описанию;
3) каждая операция или функция требуют аргументов фиксированного типа и выдают результат фиксированного типа.
В языке Pascal существуют скалярные и структурированные типы данных. К скалярным типам относятся стандартные типы и типы, определяемые пользователем. Стандартные типы включают целые, действительные, символьный, логические и адресный типы.
Целые типы определяют константы, переменные и функции, значения которых реализуются множеством целых чисел, допустимых в данной ЭВМ.
В языке Pascal принят следующий приоритет операций:
1) вычисления в круглых скобках;
2) вычисления значений функций;
3) унарные операции;
4) операции * / div mod and;
5) операции + – or xor;
6) операции отношения = <> < > <= >=.
4. Стандартные процедуры и функции
Арифметические функции
1. Function Abs(X); возвращает абсолютное значение параметра.
2. Function ArcTan(X: Extended): Extended; возвращает арктангенс аргумента.
3. Function Exp(X: Real): Real; возвращает экспоненту.
4. Function Frac(X: Real): Real; возвращает дробную часть аргумента.
5. Function Int(X: Real): Real; возвращает целочисленную часть аргумента.
6. Function Ln(X: Real): Real; возвращает натуральный логарифм (Ln е = 1) выражения Х вещественного типа.
7. Function Pi: Extended; возвращает значение Pi, которое определено как 3.1415926535.
8. Function Sin(X: Extended): Extended; возвращает синус аргумента.
9. Function Sqr(X: Extended): Extended; возвращает квадрат аргумента.
10. Function Sqrt(X: Extended): Extended; возвращает квадратный корень аргумента.
Процедуры и функции преобразования величин
1. Procedure Str(X [: Width [: Decimals]]; var S); преобразовывает число X в строковое представление.
2. Function Chr(X: Byte): Char; возвращает символ с порядковым номером Х в ASCII-таблице.
3. Function High(X); возвращает наибольшее значение в диапазоне параметра.
4. Function Low(X); возвращает наименьшее значение в диапазоне параметра.
5. Function Ord(X): Longlnt; возвращает порядковое значение выражения перечислимого типа.
6. Function Round(X: Extended): LongInt; округляет значение вещественного типа до целого.
7. Function Trunc(X: Extended): LongInt; усекает значение вещественного типа до целого.
8. Procedure Val(S; var V; var Code: Integer); преобразовывает число из строкового значения S в числовое представление V.
Процедуры и функции работы с порядковыми величинами
1. Procedure Dec(var X [; N: LongInt]); вычитает единицу или N из переменной X.
2. Procedure Inc(var X [; N: LongInt]); прибавляет единицу или N к переменной X.
3. Function Odd(X: LongInt): Boolean; возвращает True, если X – нечетное число, и False – в противном случае.
4. Function Pred(X); возвращает предыдущее значение параметра.
5. Function Succ(X); возвращает следующее значение параметра.
5. Операторы языка Pascal
Условный оператор
Формат полного условного оператора определяется следующим образом:
If B then S1 else S2
где B – условие разветвления (принятия решения), логическое выражение или отношение; S1, S2 – один выполняемый оператор, простой или составной.
При выполнении условного оператора сначала вычисляется выражение B, затем анализируется его результат: если B – истинно, то выполняется оператор S1 – ветвь then, а оператор S2 пропускается; если B – ложно, то выполняется оператор S2 – ветвь else, а оператор S1 – пропускается.
Оператор выбора
Структура оператора имеет следующий вид:
case S of
