
Полная версия:
Электроника и электротехника. Шпаргалка

Юлия Валериевна Щербакова
Электроника и электротехника. Шпаргалка
1. КЛАССИФИКАЦИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. ПОНЯТИЕ О ДВУХПОЛЮСНИКАХ.СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ
При анализе электрических цепей важно знать только параметры и способ соединения друг с другом. Активные элементы будем обозначать в основном кружочками со стрелками внутри, указывающими направление ЭДС (рис. 1); для батареи из гальванических элементов используем обозначение, приведенное на рис. 1б.
В сопротивлениях различных элементов электрических цепей происходит процесс преобразования электрической энергии в теплоту. Такие элементы называются резистивными и обозначаются прямоугольниками (см. рис. 1)
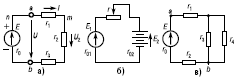
Рис. 1. Примеры схем электрических цепей
Электрические цепи постоянного тока (как и переменного) и, соответственно, их электрические схемы бывают весьма разнообразными. Так, встречаются электрические цепи неразветвленные (рис. 1а и 1б) и разветвленные (рис. 1в), с одним активным элементом (рис. 1а), с двумя (рис.1б) или с большим количеством активных элементов, линейные и нелинейные.
Линейной называется электрическая цепь, параметры которой не зависят от напряжений или токов в цепи. Если параметр хотя бы одного из элементов не остается постоянным при изменении напряжений или токов в цепи, то данный элемент и вся электрическая цепь называются нелинейными.
Часть электрической цепи, имеющая два вывода, с помощью которых она соединяется с другой частью цепи, называется двухполюсником. Различают пассивные и активные двухполюсники.
Пассивные двухполюсники содержат только пассивные элементы, активные – как пассивные, так и активные элементы. Например, справа от точек a и b на рисунке 1в расположена схема пассивного двухполюсника, соединенного с активным двухполюсником, схема которого дана слева от указанных точек. Справа и слева от точек c и d на рисунке 1 расположены схемы двух активных двухполюсников, а между этими точками – пассивный двухполюсник.
Токоведущие части различных элементов электрических цепей изготовляются из проводниковых материалов, которые бывают твердыми, жидкими и газообразными. Основными проводниковыми материалами являются металлы и их сплавы.
Если проводник имеет одну и ту же площадь поперечного сечения по всей длине, то его сопротивление равно:
где l – длина проводника, м;
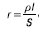
S – площадь поперечного сечения проводника, м2;
r – удельное сопротивление материала проводника, Ом/м.
Сопротивление металлических проводников при повышении температуры возрастает. Зависимость сопротивления от температуры выражается следующей формулой:
r2 = r1 [1 + α(t1 – t2)],
где t1 и t2 – начальная и конечная температуры, °С;
r1 и r2 – сопротивления при температурах t1 и t2, Ом;
α – температурный коэффициент сопротивления, °С–1.
Сведения об удельных сопротивлениях и температурных коэффициентах проводниковых материалов приводятся в справочной литературе.
2. ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ОМА И КИРХГОФА ПРИ РАСЧЕТЕ И АНАЛИЗЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Согласно закону Ома в замкнутой неразветвленной электрической цепи (рис. 2):
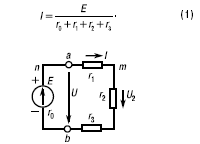
Рис. 2. Незамкнутая электрическая сеть
А в любом пассивном элементе цепи, например с сопротивлением r2,

Выражение (1) справедливо при совпадающих направлениях ЭДС Е и тока I, а выражение (2) – при совпадающих направлениях напряжения U и тока I, что и следует учитывать при нанесении на схеме стрелок, указывающих положительные направления в случае использования закона Ома.
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, соединенных в любой узловой точке электрической цепи, равна нулю, т. е.

Со знаком «+» в уравнение следует включать токи, положительные направления которых обращены к узлу, со знаком «–» – токи, положительные направления которых обращены от узла (можно и наоборот).
Согласно второму закону Кирхгофа в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех резистивных элементах контура, т. е.

Часто в электрических цепях встречаются элементы, между выводами которых имеются те или иные напряжения U (например, напряжение сети, напряжение, снимаемое с делителя напряжения, и т. д.).
Учитывая это, вместо (4) удобнее использовать следующую форму записи второго закона Кирхгофа:
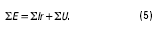
При этом ЭДС, напряжения и токи, положительные направления которых совпадают с направлением обхода контура при составлении уравнения (5), следует включать в уравнение со знаком «+», а те, положительные направления которых не совпадают с направлением обхода контура, со знаком «–» (можно и наоборот).
При составлении уравнений по второму закону Кирхгофа следует включать в них либо ЭДС и падение напряжения во внутренних сопротивлениях активных элементов, либо только их напряжения.
3. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ОДНИМ ИСТОЧНИКОМ ЭНЕРГИИ И ПАССИВНЫМИ ЭЛЕМЕНТАМИ. ПРОСТЕЙШАЯ ЦЕПЬ С ОДНИМ ПРИЕМНИКОМ
Рассмотрим простейшую неразветвленную электрическую цепь (рис. 3). В этой цепи участок amb представляет собой простейший пассивный двухполюсник, являющийся приемником электрической энергии, участок anb – простейший активный двухполюсник, являющийся источником.
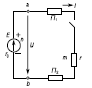
Рис. 3. Схема простейшей электрической цепи
Для рассматриваемой электрической цепи по второму закону Кирхгофа можно написать:

Из приведенных уравнений нетрудно получить формулу для определения тока и соотношение между напряжением и ЭДС источника:
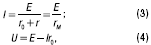
где rМ = r0 + r – эквивалентное сопротивление цепи.
При неизменных значениях ЭДС Е и внутреннего сопротивления r0 ток в цепи зависит от сопротивления r приемника. Напряжение источника U (равное в данной цепи напряжению приемника) меньше его ЭДС на падение напряжения Ir0 во внутреннем сопротивлении источника.
Если умножить (1) и (4) на ток, получим соотношения между мощностями:
EI = I2r0 + I2r; (5)
UI = EI – I2r0. (6)
Правая часть (5) содержит потери мощности во внутреннем сопротивлении I2r0 и мощность, потребляемую приемником I2r. Произведение EI представляет собой мощность, вырабатываемую источником, т. е. электрическую мощность, преобразуемую им из другого вида мощности; например, если это генератор, – из механической мощности.
Если из вырабатываемой мощности вычесть потери мощности во внутреннем сопротивлении источника I2r0, получим мощность UI, отдаваемую источником во внешнюю цепь. Мощность, отдаваемая источником в данной цепи, равна мощности, потребляемой приемником, UI = I2r. В связи с выражениями (5) и (6), а также схемой на рисунке 3 можно сделать вывод: вырабатываемая источником мощность определяется произведением тока на ЭДС, совпадающую по направлению с током, отдаваемая им мощность – произведением тока на напряжение, направленное внутри источника против тока; мощность, потребляемая приемником, определяется произведением тока на напряжение, совпадающее по направлению с током. Такие взаимные направления тока и ЭДС, а также тока и напряжения характерны для источников и приемников и в других электрических цепях. Учитывая это, выражения мощностей, вырабатываемых и отдаваемых источниками, а также потребляемых приемниками, могут быть записаны следующим образом:
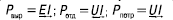
Отношение мощности, отдаваемой источником, к вырабатываемой им мощности представляет собой КПД источника:
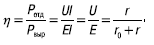
4. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ РЕЗИСТИВНЫХ ЭЛЕМЕНТОВ
Последовательным называется такое соединение элементов, когда условный конец первого элемента соединяется с началом второго, конец второго – с началом третьего и т. д. Характерным для последовательного соединения является один и тот же ток во всех элементах.
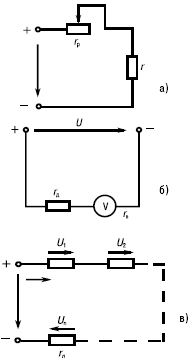
Рис. 4. Схема электрических цепей с последовательным соединением резистивных элементов
Пример: последовательно с приемником r часто включается резистор rр для регулирования напряжения, тока и мощности приемника (рис. 4а). Для расширения пределов измерения вольтметров последовательно с ними включают добавочные резисторы rд (рис. 4б). С помощью реостата, включаемого последовательно в различные ветви цепи двигателя постоянного тока, производят изменение его пускового тока или частоты вращения.
В общем случае при последовательном соединении n резистивных элементов (рис. 4в) ток в цепи, напряжения на элементах и потребляемые ими мощности определяются следующими соотношениями:
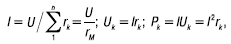
где k = 1, 2, ..., n – номер элемента;
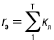
– эквивалентное сопротивление цепи.
Напряжение и мощность всей цепи:
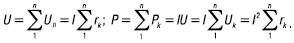
Соотношение между напряжениями, мощностями и сопротивлениями элементов:
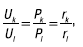
где l = 1, 2, ..., n – номер элемента.
Приемники электрической энергии последовательно, как правило, не соединяются, так как при этом требуется согласование номинальных данных приемников, исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются также остальные приемники. Чаще их включают параллельно.
5. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ РЕЗИСТИВНЫХ ЭЛЕМЕНТОВ
Параллельным называется такое соединение резистивных элементов, при котором соединяются между собой как условные начала всех элементов, так и их концы (рис. 5а). Характерным для параллельного соединения является одно и то же напряжение U на выводах всех элементов. Параллельно соединяются различные приемники электрической энергии и другие элементы электрических цепей, рассчитанные на одно и то же напряжение. При параллельном соединении не требуется согласовывать номинальные данные приемников, возможно включение и отключение любых приемников независимо от остальных, а при выходе из строя какого(либо приемника остальные остаются включенными.
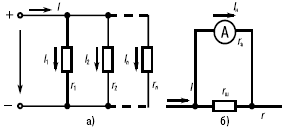
Рис. 5. Схемы электрических цепей с параллельным соединением резистивных элементов
Параллельное соединение применяется часто для расширения пределов измерения амперметров (рис. 5б): если ток I в электрической цепи превышает номинальный ток Iном амперметра, параллельно с ним включают шунтирующий резистор rш. Нередко параллельное соединение используют для уменьшения эквивалентного сопротивления какого-либо участка электрической цепи.
Токи и мощности параллельно соединенных ветвей (рис. 5а) при U = const не зависят друг от друга и определяются по формулам:
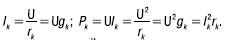
Ток и мощность всей цепи:
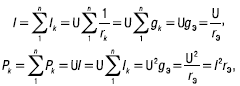
где
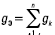
– эквивалентная проводимость;
rэ = 1 / gэ – эквивалентное сопротивление.
Соотношения между токами, мощностями, проводимостями и сопротивлениями:
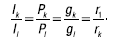
При увеличении числа параллельно соединенных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление, соответственно, уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность P; токи и мощности ранее включенных ветвей не изменяются.
6. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ,СОДЕРЖАЩИЕ СОЕДИНЕНИЯ РЕЗИСТИВНЫХ ЭЛЕМЕНТОВ ТРЕУГОЛЬНИКОМ
Под соединением треугольником (рис. 6а) понимается такое, при котором вывод К1 одного из элементов соединяется с выводом Н2 второго, вывод К2 второго – с выводом Н3 третьего, а вывод К3 третьего – с выводом Н1 первого элемента. Узловые точки a, b и c подключаются к остальной части электрической цепи.
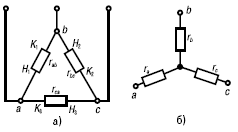
Рис. 6. Схема соединения резистивных элементов треугольником (а) и звездой (б)
Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резистивных элементов треугольником, целесообразно заменить их эквивалентными резистивными элементами, соединенными звездой (рис. 6б). Примером подобных электрических цепей являются мостовые цепи (рис. 7а). Как видно, в мостовой цепи резистивные элементы образуют два смежных треугольника (rab, rbc, rca и rbc, rbd, rdc) и нет ни одного элемента, который был бы соединен с другими последовательно или параллельно. Это осложняет расчет и анализ электрической цепи. Если заменить, например, резистивные элементы rab, rbc и rca, соединенные треугольником, эквивалентными элементами ra, rb и rc, соединенными звездой (рис. 7б), получим цепь со смешанным соединением резистивных элементов.
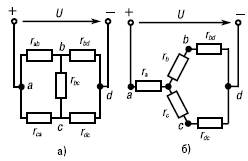
Рис. 7. Схема мостовой цепи (а) и соответствующая ей схема после замены одного из треугольников звездой (б)
Замена треугольника резистивных элементов эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками ab, bc и ca остались без изменения.
С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:
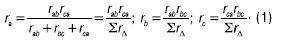
Иногда оказывается целесообразным заменить резистивные элементы, соединенные звездой, эквивалентным треугольником. Соответствующие формулы можно получить путем совместного решения выражений (1).
7. ПОНЯТИЕ ОБ ИСТОЧНИКЕ ТОКА
При расчете и анализе электрических цепей используют источники электрической энергии с параметрами E и r0, т. е. источники ЭДС, либо источники с указанными напряжениями. Иногда оказывается целесообразным заменить источник ЭДС эквивалентным ему источником тока, параметрами которого являются неизменные по значению ток короткого замыкания Ik и сопротивление r0. Рассмотрим источник тока на примере электрической цепи (см. рис. 8), в которой источник ЭДС заменим эквивалентным источником тока.
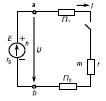
Рис. 8. Электрическая цепь
Источник тока следует считать эквивалентным в том случае, если после замены им источника ЭДС значения тока I, напряжения U и отдаваемой источником мощности UI при различных значениях сопротивления r внешней цепи остаются без изменения. Это условие будет выполнено, если источник тока будет иметь такую же внешнюю характеристику, какую имеет источник ЭДС.
Воспользуемся указанным соображением для обоснования структуры электрической цепи источника тока. Разделив левую и правую части уравнения внешней характеристики источника ЭДС на сопротивление r0, получим

где
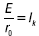
– ток короткого замыкания источника ЭДС, являющийся вместе с тем одним из параметров источника тока;
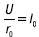
– некоторый ток, определяемый как частное от деления U на r0.
Решив (1) относительно
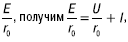
или Ik = I0 + I. (2)
Так как токи I0 и I определяются путем деления одного и того же напряжения U на соответствующие сопротивления, то в электрической цепи с источником тока должны быть две ветви с соединенными параллельно резистивными элементами r0 и r. Согласно (2) параллельно указанным ветвям должна быть включена третья ветвь, содержащая элемент с током Ik.
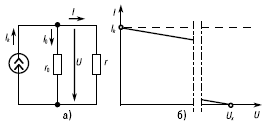
Рис. 9. Схема электрической цепи
Схема электрической цепи, эквивалентная приведенной на рисунке 8, но содержащая источник тока, дана на рисунке 9а. Элемент с током I в совокупности с резистором r0 и представляет собой источник тока:
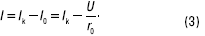
Получили уравнение внешней характеристики
I(U) источника тока. Уравнение (3) и внешняя характеристика, построенная с помощью этого уравнения (рис. 9б), дадут при любом режиме работы цепи такие же значения тока I и напряжения U, как и в случае источника ЭДС.
8. МЕТОД ЗАКОНОВ КИРХГОФА. МЕТОД КОНТУРНЫХ ТОКОВ
Покажем на схеме положительные направления известных и неизвестных величин. Сначала следует составить более простые уравнения по первому закону Кирхгофа, максимальное число которых должно быть на единицу меньше числа узловых точек. Недостающие уравнения следует составить по второму закону Кирхгофа.
В качестве примера составим схему уравнений для определения токов в электрической цепи, схема которой изображена на рисунке 10. Будем считать, что ЭДС и напряжения с их направлениями, а также сопротивления известны. Поскольку данная цепь имеет пять ветвей с неизвестными токами, необходимо составить пять уравнений. Выбрав положительные направления токов I1, I2, I3, I4 и I5 для узлов а и б, а также для контуров агда, абга и бвгб при обходе последних по часовой стрелке, получим:
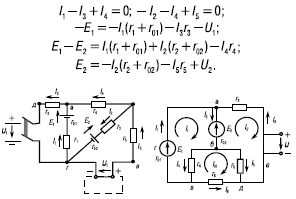
Рис. 10. К расчету разветвленных электрических цепей с помощью законов Кирхгофа
Рис. 11. К пояснению метода контурных токов
Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом законов Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно.
Любая разветвленная электрическая цепь состоит из нескольких смежных контуров. Например, в электрической цепи (рис. 10) таких контуров три: абвга, бдвб и аедба. Каждый контур имеет несмежные ветви, принадлежащие лишь данному контуру, и смежные ветви, принадлежащие также соседним контурам. Так, контур абвга имеет несмежную ветвь вга и две смежные ветви аб и бв.
Допустим, что в каждом контуре (рис. 11) имеется некоторый контурный ток, одинаковый для всех элементов контура. На рисунке 11 контурные токи обозначены II, III и IIII. Положительные направления контурных токов могут быть выбраны произвольно. Наложим на контурные токи следующее условие: контурные токи должны быть равны по абсолютному значению токам несмежных ветвей соответствующих контуров.
Если выбрать положительное направление тока несмежной ветви совпадающим с контурным током, то ток ветви должен быть равен контурному току; если же направить ток несмежной ветви против контурного тока, то он должен быть равен контурному току со знаком «–».
Так, токи в несмежных ветвях цепи будут равны:II = II; I3 = –III; I6 = – IIII;
I2 = I1 + I3 = II – III ; I4 = II + IIII; I5 = IIII + III.
Видно, что со знаком «+» должен быть взят тот контурный ток, направление которого совпадает с направлением тока смежной ветви; контурный ток, направленный в противоположную сторону, должен быть взят со знаком «–».
Уравнение по второму закону Кирхгофа при включении в него контурных токов в общем случае имеет вид:
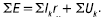
Для рассматриваемой цепи (рис. 11) уравнения будут:
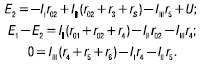
9. МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ
Метод узлового напряжения дает возможность просто произвести анализ и расчет электрической цепи, содержащей несколько параллельно соединенных активных и пассивных ветвей, например цепи, схема которой изображена на рисунке 12.
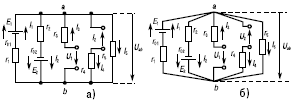
Рис. 12. Схема электрической цепи
Пренебрегая сопротивлением проводов, соединяющих ветви цепи, схему (рис. 12а) можно заменить более удобной для рассмотрения (рис. 12б).
В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей между узловыми точками а и b установится определенное узловое напряжение Uab. Предположим, что оно направлено так, как показано на рисунке 12, и известно. Зная напряжение Uab, легко найти все токи.
Выберем положительные направления токов, например так, как показано на рисунке. Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви,
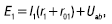
откуда:
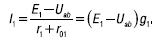
Поступая аналогичным способом, нетрудно получить формулы для токов I2, I3 и I4:
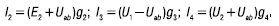
По закону Ома для пятой ветви:
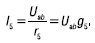
Для вывода формулы, позволяющей определить напряжение Uab. Преобразуем формулу по первому акону Кирхгофа:
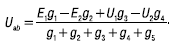
Формула узлового напряжения в общем случае имеет вид:
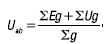
Перед определением напряжения по последней формуле следует задаться его положительным направлением. Со знаком «+» должны входить ЭДС, направленные между точками а и b встречно напряжению Uab, и напряжения ветвей, направленные согласно с Uab. Знаки в последней формуле не зависят от направления токов и ветвей.
При анализе и расчете электрических цепей методом узлового напряжения целесообразно выбирать положительные направления токов после определения узлового напряжения. В этом случае положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.



