
Полная версия:
Тяжелосредное обогащение углей

Введение
Из всех гравитационных методов обогащения наиболее высокую технологическую эффективность имеют методы, основанные на применении суспензий минеральных порошков в качестве разделительной среды. Этот способ обогащения позволяет получить результаты разделения по плотностям, близкие к теоретическим, свести к минимуму потери угля с отходами обогащения и обеспечить получение высококачественных товарных продуктов. Кроме того, в тяжелых суспензиях может обогащаться уголь с широким диапазоном крупности – от практически 0(0,1) мм в гидроциклонах и до 350–400 мм в тяжелосредных сепараторах при практически неограниченном содержании тяжелых фракций.
Аппараты тяжелосредного обогащения малочувствительны к колебаниям нагрузок и зольности исходного угля, они просты в регулировании и обеспечивают получение концентрата стабильного качества.
Указанные преимущества этого метода обогащения создали предпосылки для его широкого внедрения на углеобогатительных фабриках.
Технологический комплекс для обогащения углей в суспензиях минеральных порошков значительно отличается от широко применявшихся и хорошо освоенных обогатительных комплексов для отсадки и флотации. Тяжелосредный комплекс отличается как по составу оборудования, так и по своим эксплуатационным особенностям, обусловленным применением суспензии минеральных порошков в качестве разделительной среды. Машины и аппараты, применяемые для данного метода обогащения, характеризуются разнообразием конструктивного исполнения, а также физическими основами, заложенными в принцип их работы. Так, при обогащении крупных классов угля в сепараторах используется гравитационный принцип разделения, мелкие классы, обогащаемые в гидроциклонах, разделяются по плотности в поле действия центробежных сил, а для регенерации суспензии используется магнитное силовое поле.
Наряду со специфическим оборудованием, применяемым только при обогащении в суспензиях минеральных порошков, в технологический комплекс тяжелосредного обогащения входят машины и аппараты общетехнического назначения (грохоты, насосы, компрессоры, смесители), однако их эксплуатация и наладка также носят специфический характер, связанный с применением в качестве разделительной среды магнетитовой суспензии.
Обслуживание технологических тяжелосредных комплексов требует от рабочих и инженерно-технического персонала высокой квалификации, умения применять научно обоснованные нормативные параметры и прогрессивные способы управления технологическим процессом обогащения с использованием средств автоматизации. Особенно ответственные и сложные задачи возникают при пуске и первичной наладке тяжелосредных комплексов на вновь построенных и реконструируемых фабриках, где обогащение в тяжелых средах осваивается впервые и эксплуатационный персонал еще не имеет достаточного практического опыта по выполнению пуско-наладочных работ и оперативной регулировке оборудования, входящего в тяжелосредный комплекс. Тем более что появляются углеобогатительные фабрики, обогащающие угли только в тяжелосредных гидроциклонах с магнетитовой суспензией несколькими машинными классами. Возможно, такой и будет углеобогатительная фабрика будущего.
В настоящей монографии авторы ставят задачу изложить основные принципы технологии тяжелосредного обогащения угля в магнетитовой суспензии на основе современных представлений и передового производственного опыта.
Глава 1. Тяжелосредное обогащение как технологический процесс
1.1. Общие сведения
1.1.1. Преимущества тяжелосредного обогащения углей
При обогащении угля в обогатительных аппаратах происходит разделение компонентов по двум-трем признакам: плотности, крупности и смачиваемости. Такая многофункциональность затрудняет получение максимальной технологической эффективности. Сведение на нет всех остальных разделительных признаков, кроме одного (нужного), является основной задачей построения технологического процесса.
На рис. 1.1 приведены сепарационные характеристики при действии одного (а) и двух (б) разделительных процессов, из которых следует, что в первом случае Еpm может быть почти в два раза меньше, чем во втором.
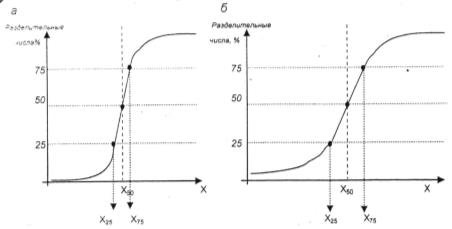
Рис. 1.1. Сепарационная характеристика при действии одного (а) и двух (б) разделительных признаков
Такое утверждение согласуется с законами термодинамики, согласно которым всякая система стремится к равновесию, при этом по одному параметру систему легче привести в равновесие, нежели по нескольким параметрам одновременно.
Разделение угля в тяжелых жидкостях служит примером однофункционального процесса, в котором сепарация осуществляется по контрастности в плотностях полезного и неполезного компонентов. Наличие тонкодисперсных шламов ухудшает сепарационные характеристики тяжелосредных сепараторов, но это вовсе не означает, что крупность перерабатываемого материала является разделительным признаком. Высокодисперсные шламы приводят к изменению свойств разделительной среды: повышают ее вязкость и плотность.
Обогащение по одному разделительному признаку – плотности разделяемых частиц – позволяет добиться максимальной эффективности гравитационного обогащения прежде всего потому, что сводится к минимуму влияние крупности обогащаемого материала. Приводим технологические возможности типичного разделительного оборудования по величине средневероятного отклонения Еpm в кг/м3 в зависимости от плотности разделения и крупности обогащаемого материала в табл. 1.1 [1, 2].
Таблица 1.1
Технологические возможности углеобогатительного оборудования
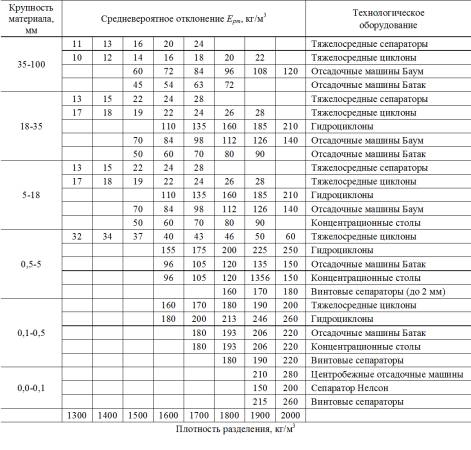
Взаимозасорение продуктов разделения достигает минимального уровня при разделении по одному признаку в широком диапазоне крупности. Как видно из представленной табл. 1.1 вплоть до ультратонкой крупности 0,1 мм тяжелосредная сепарация значительно опережает по эффективности другие процессы типа гидравлической отсадки в отсадочных машинах Баум и Батак, гидроциклонирования, мокрой винтовой сепарации (МВС), концентрации на столах.
На рис. 1.2 графически показана диаграмма суммарной засоренности концентрата и породы при обогащении угля средней обогатимости на различных аппаратах [3]. Наименьшая засоренность достигается в тяжелых средах. Засоренность продуктов обогащения отсадочных машин несколько выше. Остальные обогатительные аппараты выпускают концентрата и породу со значительно большей суммарной засоренностью.
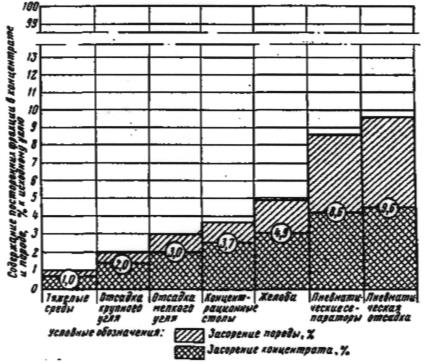
Рис. 1.2. Диаграмма суммарной засоренности концентрата и породы при обогащении угля средней обогатимости на различных аппаратах
При обогащении крупнозернистого шлама эффективность технологического действия различных процессов приведена на рис. 1.3 [4]. Из рис. 1.3 следует, что в диапазоне крупности наибольшую технологическую эффективность при обогащении шламов имеют тяжелосредные гидроциклоны. В диапазоне 0,35-1 мм предпочтение отдается мокрой винтовой сепарации при обогащении диапазона менее 0,35 мм на первое место выходит флотации.
Таким образом, процесс разделения минералов в тяжелых средах стал неотъемлемой частью технологии обогащения углей и все больше вытесняет другие гравитационные методы при модернизации старых и строительстве новых углеобогатительных фабрик.
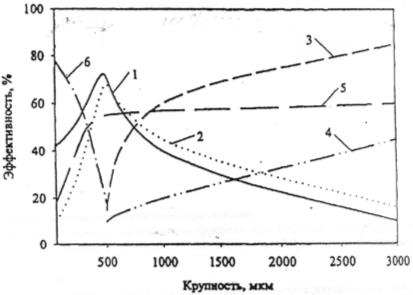
Рис. 1.3. Диапазон эффективного технологического действия различных процессов при обогащении угольной мелочи (по Дюпрену):
1 – винтовые сепараторы; 2 – концентрационные столы; 3 – тяжелосредные циклоны; 4 – отсадка; 5 – гидроциклоны; 6 – флотация
Анализ технологических схем вновь строящихся углеобогатительных фабрик как в Украине [5], так и за рубежом [6, 7], а также материалы XVI и XVII конгрессов по углеобогащению [8, 9] свидетельствуют, что для обогащения мелкого машинного класса угля повсеместно используются только тяжелосредные гидроциклоны с магнетитовой суспензией. Целесообразность их применения вместо гидравлических отсадочных машин подтверждается известными данными по значениям Еpm для этого оборудования. Так, по данным статьи [1], при низкой плотности разделения (1600 кг/м3) разность в значениях Еpm для отсадочной машины Батак и тяжелосредного гидроциклона для крупности 35-100 мм составляет 54–16 = 38 кг/м3, для крупности 18-5 мм – 60–22 = 38 кг/м3, для крупности 5-18 мм – 66–22 = 44 кг/м3, для крупности 0,5–5 мм – 96–40 = 56 кг/м3. Тоже при высокой плотности разделения 1800 кг/м3 соответственно 72–20 = 52; 80–26 = 54; 84–24 = 60; 120 – 46 = 74 кг/м3.
Исходя из проведенных по этим данным расчетов [10], можно прогнозировать снижение потерь горючей массы при обогащении мелкого машинного класса по любой плотности разделения практически в 2 раза. Следовательно, с технологической точки зрения замена гидравлической отсадки на операции обогащения мелкого угля на тяжелосредные гидроциклоны целесообразна. Естественно, что эта замена должна проводиться в первую очередь на углеобогатительных фабриках, применяющих тяжелосредные сепараторы для обогащения крупного машинного класса.
Развитие техники и технологии тяжелосредного обогащения угля позволяет увеличивать глубину обогащения практически до 0 мм. В этих случаях обесшламливание мелкого машинного класса не производится [11, 12], однако значительно увеличивается фронт регенерации суспензии и регенерации оборотной воды. Таким образом, в ближайшей перспективе могут появиться тяжелосредные фабрики, обогащающие угли только в гидроциклонах с магнетитовой суспензии.
1.1.2. Термины и определения
Обогащение в тяжелых средах – метод разделения углей по плотности в истинных тяжелых жидкостях или минеральных суспензиях.
Истинные тяжелые жидкости – водные растворы неорганических солей и органические жидкости – в производственных условиях имеют ограниченное применение. Их используют в основном для разделения углей по плотности при фракционном анализе и контроле качества продуктов обогащения.
Взвеси в воде тонкоизмельченных утяжелителей – минеральные суспензии – широко распространены во всем мире в качестве разделяющей среды при обогащении углей.
В отечественной и зарубежной практике применяют преимущественно минеральные суспензии, в которых в качестве утяжелителя используют магнетитовый концентрат, позволяющий получать плотность разделяющей среды, достаточную для успешного обогащения всех видов твердых горючих ископаемых (каменных и бурых углей, антрацитов, горючих сланцев).
В некоторых странах в качестве утяжелителей в ограниченных масштабах используют барит, кварцевый песок, глину, лёсс и другие материалы, однако эти утяжелители не выдерживают конкуренции с магнетитом.
Следует отметить следующие особенности метода обогащения в тяжелых средах:
простоту регулирования и широкую возможность автоматизации производственного процесса;
малую чувствительность к колебаниям нагрузки (в пределах нагрузочной устойчивости оборудования) и качественного состава питания;
возможность эффективного обогащения углей с трудной и очень трудной характеристикой обогатимости и высоким содержанием свободной породы;
возможность разделения обогащаемого сырья в широком диапазоне крупности – от самых крупных штучных кусков (размером 500 мм и более) до мелкого материала (примерно до 0,2–0,5 мм и менее);
высокую точность разделения, обеспечивающую минимальное засорение конечных продуктов посторонними фракциями;
широкий диапазон изменения плотности разделения (от 1300–1350 до 2000–2200 кг/м3) с предельно точной регулировкой плотности разделяющей среды;
незначительное шламообразование в обогатительных аппаратах, возможность удаления размокающей породы в начале технологического процесса;
наименьший (по сравнению с другими мокрыми процессами обогащения) расход технологической воды.
Перечисленные достоинства тяжелосредного метода обогащения относятся к технологии обогащения как крупного, так и мелкого угля и угольного шлама. Обогащение крупного угля в магнетитовой суспензии осуществляется в тяжелосредных сепараторах, мелкого угля и угольного шлама – в тяжелосредных гидроциклонах.
Условия разделения частиц обогащаемого угля в тяжелой среде определяется соотношением сил, действующих на частицу: силы тяжести Fg и подъемной (архимедовой) силы FА, с учетом сил сопротивления среды и механического взаимодействия частиц при их соприкосновении. Равнодействующая G сил, действующих на частицу в неподвижной среде:

С учетом того, что Fg = Vδчg и FА = Vδсg, где V – объем частицы; δч и δч – плотность частицы и среды; g – ускорение свободного падения, получим

Возможны три условия разделения частиц: δч > δс; δч < δс и δч = δс. В первом случае G > 0 и частица тонет, во втором G < 0 и частица всплывает, в третьем G = 0 и частица находится во взвешенном состоянии.
С уменьшением размеров зерен снижается разность скоростей их падения и резко возрастает время, необходимое для их разделения.
Интенсифицировать процесс обогащения мелких зерен угля можно в поле действия центробежных сил, возникающих при вращательном движении суспензии. Центробежную силу Fц, действующую на частицу, определяют по формуле

где m – масса частицы; ω – окружная скорость вращения; r – радиус вращения; ω2/r – центробежное ускорение.
С учетом того, что m = Fg /g и ω = 2πrn/60, где n – частота вращения, получим

Подставив числовые значения для π и g, окончательно получим

Из полученного выражения следует, что значение центробежной силы в значительно большей степени зависит от частоты вращения суспензии, чем от радиуса вращения тела.
Для разделения мелкого угля по плотности в центробежном поле используют тяжелосредные гидроциклоны. Мелкий уголь вместе с суспензией (с определенной скоростью и под давлением) тангенциально вводят в гидроциклон. Плотность разделения угля в тяжелосредном гидроциклоне может быть равной ил выше плотности суспензии, подаваемой в него вместе с углем. Частицы угля, плотность которых меньше плотности разделения, удаляются из гидроциклона вместе с суспензией через сливной патрубок, а частицы с большей плотностью разгружаются через песковую насадку гидроциклона.
Плотность разделения в тяжелосредном сепараторе соответствует плотности магнетитовой суспензии, подаваемой в сепаратор.
Плотность разделения в тяжелосредном двухпродуктовом гидроциклоне может превышать плотность магнетитовой суспензии примерно на 20 % за счет расслоения утяжелителя.
Степень расслоения частиц утяжелителя зависит также от продолжительности пребывания суспензии в гидроциклоне. При большой скорости протекания суспензия не успевает полностью расслоится.
В трехпродуктовых тяжелосредных гидроциклонах превышение плотности разделения во второй ступени может достигать, в сравнении с плотностью разделения в первой, примерно на 400–500 кг/м3.
Для ориентировочного расчета разности плотностей между I и II ступенями разделения в трехпродуктовом тяжелосредном гидроциклоне В.И. Хайдакин предложил эмпирическую формулу

где S0 – параметр, характеризующий степень сгущения суспензии и зависящий от размера частиц утяжелителя, содержания шлама в суспензии, ее плотности и давления на входе в гидроциклон.
Для магнетита марки «М» (средний взвешенный диаметр зерна утяжелителя 40–50 мкм) S0 определяется эмпирическим соотношением
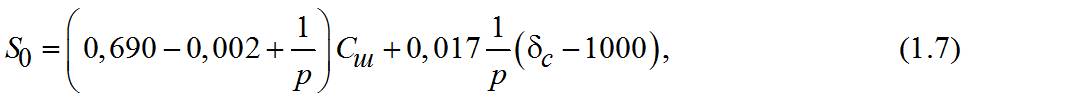
где p – давление на входе в циклон, МПа; Сш – содержание шлама в суспензии, кг/м3; δс – плотность суспензии, кг/м3.
Наиболее рациональные области применения тяжелосредного обогащения:
крупные классы углей для коксования и энергетики и антрациты (от 13–25 до 200–300 мм) очень трудной, трудной, средней и легкой обогатимости при содержании породных фракций (плотностью +1800 кг/м3 – для углей, +2000 кг/м3 – для антрацитов) более 35 % и выходе класса >13 мм более 20 % с разделением на три и два продукта;
крупные классы (>25 мм) сланцев;
мелкие классы углей для коксования (от 0,2–0,5 до 13; 25; 40 мм) трудной и очень трудной обогатимости с разделением на три продукта;
мелкие классы энергетических углей трудной и очень трудной обогатимости и антрациты (от 0,5 до 13(25) мм) с разделением на два продукта;
промпродукты отсадки крупных (после додрабливания) и мелких каменных углей и антрацитов (0,5-13 мм) с разделением на три и два продукта.
Тяжелосредное обогащение твердых горючих ископаемых может производиться также с целью получения продуктов высокого качества для специальных целей, например, антрацитовых концентратов для электродной промышленности, малосернистых угольных концентратов, сланцевых концентратов с повышенным содержанием органической массы.
1.1.3. Характеристика тяжелой среды
В качестве тяжелой среды при обогащении полезных ископаемых по плотности применяют суспензии, которые приготовляют из смеси тонкоизмельченных твердых частиц и воды. Следовательно, твердые частицы являются дисперсной фазой, которую называют утяжелителем. Дисперсионной фазой является вода. Содержащиеся в суспензии твердые частицы поддерживаются в состоянии движения энергией жидкости и потенциальной энергией поверхностного натяжения.
В качестве утяжелителя используют измельченные до крупности менее 0,1 мм различные минералы (иногда смесь минералов), (табл. 1.2).
Таблица 1.2
Характеристика утяжелителей и суспензии
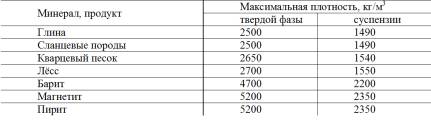
Суспензии могут быть разделены на три группы: устойчивые (колоиднодисперсные), неустойчивые (грубодисперсные) и стабилизированные, т. е. системы, устойчивость которых достигается путем применения величальных мер, сопровождающихся затратой энергии.
В практике обогащения угля применяют главным образом стабилизированные суспензии. Относительно ограниченное применение получили неустойчивые суспензии.
Стабилизация суспензий может быть произведена следующими способами:
1) применением соответствующего утяжелителя;
2) добавлением в суспензию материалов, обладающих коллоидными свойствами;
3) применением восходящих потоков;
4) механической активацией суспензии;
5) горизонтальным перемещением суспензии.
Первые два способа дают возможность получить статически устойчивую суспензию, а остальные – динамически устойчивую. Результаты обогащения углей в статически устойчивых суспензиях несколько лучше, чем в динамически устойчивых. Однако наибольшее распространение в настоящее время получили динамически устойчивые суспензии, стабилизированные их горизонтальным перемещением.
Если не предусмотрены специальные меры для стабилизации суспензии и она оставлена в состоянии покоя, то утяжелитель быстро осаждается. Через небольшой промежуток времени образуется значительная разница в плотностях выше- и нижележащих зон суспензии.
Уголь, погруженный в суспензию, расслаивается по плотности: частицы угля, плотность которых меньше плотности суспензии в верхней зоне, всплывают, а частицы, плотность которых больше плотности суспензии в нижней зоне, опускаются на дно ванны. В промежуточном слое суспензии находятся во взвешенном состоянии частицы угля промежуточной плотности. Следовательно, в суспензии в одном аппарате можно получить три продукта обогащения: концентрат, промежуточный продукт и породу.
Плотность суспензии по высоте ванны можно изменять, меняя скорость продольного перемещения суспензии и крупность утяжелителя.
Суспензии должны быть эффективны для широких пределов крупности обогащаемого угля, не обладать большой вязкостью при принятой плотности разделения, а также корродирующими и токсичными свойствами. Этим требованиям удовлетворяет суспензия, содержащая 25–35 % твердых веществ высотой плотности (утяжелителя) по объему. Приготовление суспензии, обладающей перечисленными свойствами, является нелегкой задачей.
Содержание твердой фазы в суспензии при обычно применяемой плотности разделения в первую очередь зависит от плотности утяжелителя. Следовательно, свойства суспензии определяются главным образом плотностью и размером частиц твердой фазы.
Если для обогащения угля применяется суспензия, образованная магнетитом, то приемлемая текучесть и необходимая плотность суспензии могут иметь место даже в том случае, когда в суспензии находится значительное количество угля и глины. Однако если суспензия приготовляется из смеси барита и глины, необходимо самое тщательное отделение угольного шлама от утяжелителя.
В промышленных условиях для приготовления суспензий в качестве утяжелителей применяют минералы и некоторые отходы различных видов производства. Проводятся также работы с целью применения в качестве утяжелителя искусственно приготовленных минералов (гуммированные металлические зерна).
Утяжелитель должен удовлетворять следующим основным требованиям:
1) обеспечивать возможность приготовления маловязкой суспензии плотностью 1,3–2,0 т/м3. Для этого плотность утяжелителя должна примерно втрое превышать заданную плотность суспензии;
2) быть химически инертным по отношению к воде и обладать сопротивлением истиранию;
3) легко отделяться от угольного и глинистого шлама;
4) легко отделяться от продуктов обогащения при промывке их на грохотах и от промывной воды в сгустителях;
5) обеспечивать возможность стабилизации суспензии простейшими средствами.
Из природных материалов в качестве утяжелителей для образования суспензий, в которых производят обогащение угля, применяют барит, гематит, магнетит и пирит (табл. 1.3).
Таблица 1.3
Характеристика основных минералов, применяемых для приготовления суспензий
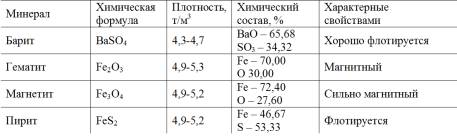
В практике обогащения углей преимущественное распространение получили магнетитовые суспензии, утяжелителем в которых является магнетит.
К преимуществам магнетита относятся: сравнительно низкая стоимость, высокая плотность, малая истираемость, пригодность к применению без дополнительной доводки до кондиции, удовлетворяющей техническим требованиям к утяжелителю, недефицитность. Регенерация его в магнитных сепараторах проста и достаточно эффективна.
1.2. Магнетит
1.2.1. Характеристика магнетитовых руд
В связи с широким развитием тяжелосредного обогащения твердых горючих ископаемых (уголь, антрацит) важное значение приобретает выбор магнетитовых концентратов, применяемых в качестве утяжелителей для приготовления суспензий.
Качество магнетитовых концентратов определяется как технологией обогащения, так и качеством железистых магнетитовых руд.
Железистые магнетитовые руды, сформировавшиеся в различных геологических условиях, отличаются разнообразием минерального состава, текстурно-структурным строением, физических свойств, которые определяют технологические параметры обогащения для каждой руды.
Основной рудный минерал магнетитовых руд – магнетит, подчиненное значение могут иметь гематит, мартит*, пирротин, пирит, халькопирит, кобальтин, сфалерит, галенит, марказит, арсенопирит.
В чистом магнетите (FeO · F2O3) содержится 72,4 % железа, стехиометрическое соотношение двухвалентного и трехвалентного железа 1:2, плотность 4900–5200 кг/м3, твердость по шкале Мооса – 5,5–6,0 единиц. Природные магнетиты отличаются существенным содержанием примесей различных элементов и соответственно сложным химическим составом. Содержание железа в них изменяется в широких пределах.
Условно месторождения магнетитовых руд делят на две группы: с относительно чистым магнетитом и с магнетитом, содержащим изоморфные и дисперсные примеси. Например, в рудах, добываемых горно-обогатительными комбинатами Криворожского бассейна и КМА, имеющих осадочно-метаморфическое происхождение, собственно магнетита присутствует от 29,4 до 40 %, гематита (мартита) – от 1,5 до 7,0 %. Содержание железа колеблется от 31,1 до 35,6 %.



