
Полная версия:
Объектно-ориентированное программирование на Java. Платформа Java SE

Объектно-ориентированное программирование на Java
Платформа Java SE
Тимур Машнин
© Тимур Машнин, 2024
ISBN 978-5-0050-3960-6
Создано в интеллектуальной издательской системе Ridero
Введение

На этом курсе мы будем изучать технологию Java.
Итак, что такое технология Java?
Начнем с самого понятия технологии программирования.

Можно сказать, что технология программирования – это совокупность методов и инструментов, позволяющих создавать программное обеспечение.
Технологии программирования могут иметь различный уровень применения. В процессе разработки программного обеспечения могут применяться технологии, решающие как конкретные задачи, так и технологии, являющиеся платформой для создания частей приложения или всего приложения.
Поэтому, как правило, для создания программного обеспечения применяется целый набор различных технологий.
Применительно к Java, технология Java – это язык программирования Java и платформа Java.
Язык программирования Java представляет собой объектно-ориентированный язык программирования, имеющий синтаксис, близкий к синтаксису языка С++.
Отличия языка Java от языка С++ обусловлены самим происхождением этих языков программирования.
Язык С++ является расширением языка С, который создавался как язык системного программирования.

Язык Java, в свою очередь, создавался для решения задач сетевого программирования и является самостоятельным языком программирования.
Главные отличия языка Java от языка С++ – это более строгая типизация, ограничения работы с памятью, автоматическая сборка мусора.
Понятно, что для создания программного обеспечения наличие одного языка программирования недостаточно.
Для компилируемых языков нужны инструменты, компилирующие исходный код в машинный, исполняемый операционной системой компьютера.
Для интерпретируемых языков программирования необходимы интерпретаторы, выполняющие исходный код в операционной системе.
В случае языка Java, реализация платформы Java как раз и обеспечивает выполнение Java-кода в операционной системе компьютера.
Таким образом, для того чтобы Java-приложение могло быть запущено, необходима реализация платформы Java.
Мы упомянули реализацию платформы Java.
Что это такое?
Платформа Java состоит из виртуальной машины Java Virtual Machine (JVM) и библиотек интерфейса программирования Java Application Programming Interface (API).

Для всех распространенных операционных систем существуют свои виртуальные машины JVM, тем самым реализуется принцип «Write Once, Run Anywhere» – написанное однажды, работает везде.
Реализация платформы Java – это конкретная реализация JVM для конкретной операционной системы плюс библиотеки Java API.
На самом деле компанией Oracle для выполнения Java-приложений предоставляется набор сред выполнения Java Runtime Environment (JRE), охватывающий все распространенные операционные системы.
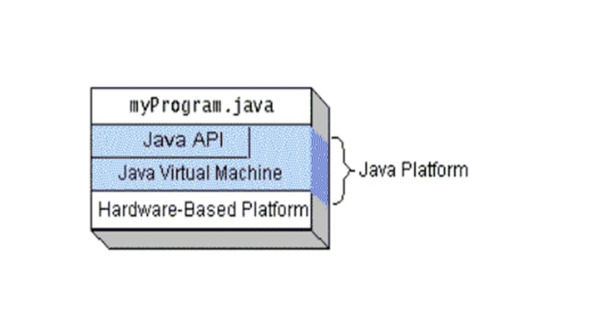
Виртуальная машина JVM составляет основную часть среды выполнения Java Runtime Environment (JRE).
Помимо JVM JRE содержит базовые библиотеки API, необходимые для выполнения Java-приложений, а также дополнительные инструменты, включая Java Plug-in – для запуска апплетов в браузере и Java Web Start – для развертывания Java-приложений через Интернет.
Компанией Oracle также предоставляется минимальный комплект разработки Java-приложений Java Development Kit (JDK), состоящий из набора инструментов, включая компилятор в байт-код javac, документации, примеров и среды выполнения JRE.
Язык программирования Java является одновременно и интерпретируемым, и компилируемым. Причина этого кроется в устройстве виртуальной машины JVM.
Виртуальная машина JVM – это набор специальных программ, созданных для конкретной операционной системы.
Точкой входа в виртуальную машину JVM является программа java, запускающая Java-приложение.
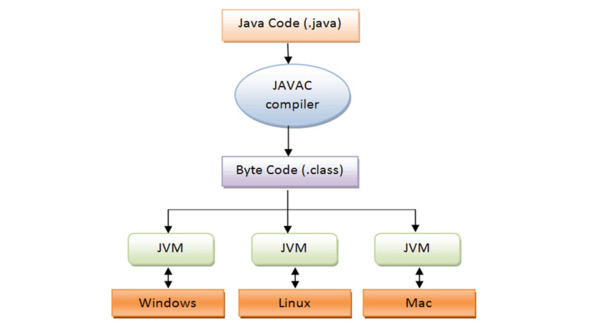
Приложения, написанные на языке Java, представляют собой текстовые файлы с расширением. java.
Чтобы JVM выполнила Java-приложение, приложение должно быть откомпилировано в специальный двоичный формат – байт-код.
Откомпилированное Java-приложение состоит из файлов с расширением. class, которые могут быть упакованы в архивный исполняемый файл с расширением. jar.
При запуске Java-приложения на вход JVM подается байт-код Java-приложения, а также байт-код используемых приложением библиотек Java API.
Виртуальная машина JVM может выполнять приложения, написанные и на других языках программирования – Scala, Groovy, Ruby, PHP, JavaScript, Python и др., при этом приложения также должны быть откомпилированы в байт-код.
В процессе обработки байт-кода виртуальная машина JVM производит его интерпретацию, т.е. выполняет команды, содержащиеся в байт-коде, или использует компилятор Just-in-time compilation (JIT), который транслирует байт-код в машинный код непосредственно во время выполнения Java-приложения, и тем самым увеличивает скорость обработки байт-кода.
Таким образом, язык Java является компилируемым, потому что необходима компиляция исходного кода в промежуточный по отношению к машинному байт-коду, и интерпретируемым, потому что байт-код не может быть исполнен самой операционной системой компьютера, а должен интерпретироваться.
Платформа Java содержит два типа JVM:
Java HotSpot Client VM (Client VM). Вызывается опцией – client инструмента java и обеспечивает быстрый запуск и потребление небольшого объема оперативной памяти.

Java HotSpot Server VM (Server VM). Вызывается опцией —server инструмента java и обеспечивает максимальную скорость выполнения приложения.
Для обеих JVM технология Java HotSpot оптимизирует обработку байт-кода, распределение памяти, сборку мусора и управление потоками.
Технология Java – это общее понятие, на самом деле обозначающее широкий спектр Java-технологий.
Среда выполнения JRE и комплект разработки JDK являются основными продуктами платформы Java Platform, Standard Edition (Java SE).
Как уже было сказано, платформа Java содержит библиотеки интерфейса программирования Java API. Для чего они предназначены и какую роль они выполняют?
Библиотеки Java API – это готовые классы и интерфейсы, обеспечивающие для создаваемых Java-приложений общую функциональность.

С библиотеками Java API программисту не нужно самому реализовывать ввод-вывод, сетевое соединение, создавать стандартные графические компоненты для интерфейса пользователя и многое-многое другое.
Все это уже предоставлено технологией Java.
Платформа Java SE является основой для всех остальных платформ технологии Java. Все вместе Java-платформы обеспечивают применение технологии Java к широкому диапазону устройств – от смарт-карт, встроенных и мобильных устройств до серверов и суперкомпьютеров.
Технология Java представлена следующими платформами:
Java Platform, Standard Edition (Java SE) – предоставляет среду выполнения и набор технологий и библиотек API для создания и запуска серверных и настольных приложений, апплетов и является основой для остальных платформ.

Кроссплатформенность обеспечивается наличием сред выполнения для различных операционных систем.
Платформа Java SE включает в себя следующие компоненты – среду выполнения Java Runtime Environment (JRE) и комплект разработчика приложений Java Development Kit (JDK).
Java SE Embedded – предназначена для встроенных систем, таких как интеллектуальные маршрутизаторы и коммутаторы, профессиональные принтеры и др.
Платформа Java SE for Embedded обеспечивает ту же функциональность, что и платформа Java SE, дополнительно добавляя поддержку для платформ, специфических для встроенных систем, оптимизацию использования памяти, а также предоставляя уменьшенную среду выполнения и опцию Headless для устройств, не имеющих дисплея, мышки или клавиатуры.
Java Platform, Micro Edition (Java ME) – содержит набор сред выполнения и библиотек API, предназначенных для встроенных и мобильных устройств. В настоящее время активно применяется для Интернет вещей.
Java Card – позволяет создавать и запускать небольшие приложения (Java Card-апплеты) в смарт-картах и других устройствах с очень ограниченными ресурсами, таких как SIM-карты мобильных телефонов, банковские карточки, карты доступа цифрового телевидения и др.
Java Platform, Enterprise Edition (Java EE) – является расширением платформы Java SE и добавляет библиотеки, позволяющие создавать распределенные, многоуровневые серверные Java-приложения.
Если сравнивать язык Java с такими распространенными языками как С#, JavaScript, Python и PHP,
То сравнивая Java c C#, который работает на платформе NET, c точки зрения разработчика языки Java и C# очень похожи.
Но у них есть некоторые синтаксические различия, и язык Java считается более простым языком.
Кроме того, C# все таки больше привязан к платформе Windows.
Так как эти два языка очень похожи, при их сравнении возникают большие дискуссии, в которые мы сейчас углубляться не будем.
Если сравнивать Java и JavaScript, язык JavaScript является только интерпретируемым и выполняется только в веб-браузерах.
Если сравнивать Java и Python, то Python также является компилируемым и интерпретируемым языком, но с полной динамической типизацией, он проще в изучении, но проигрывает в скорости Java, хотя для него есть альтернативные реализации интерпретаторов: Jython, Cython и другие.
По поводу сравнения Java и Python также ведутся жаркие дискуссии.
Если сравнивать Java и PHP, то PHP это скриптовый серверный язык для разработки веб приложений, он проще в изучении и является языком с динамической типизацией. PHP не предназначен для крупных проектов, однако, PHP хостинг более распространен, чем для Java.
Как видно у каждого языка есть свои плюсы и минусы, но «Вы должны писать на языке, который делает вас счастливее», как сказал Пэт Аллан.
Выражения

Теперь каким способом можно хорошо представить, что такое компьютер?
И какие есть концепции языка программирования?
Вместо того, чтобы начинать с нуля, мы начнем с устройства, которое вам очень хорошо известно, а именно, калькулятора.
И мы постепенно преобразуем простой калькулятор в компьютер.
Сделав это, мы также перейдем от ввода последовательности клавиш калькулятора к компьютерной программе.
Таким образом, вы гораздо лучше поймете концепции, на которых основывается компьютер и языки программирования, такие как Java.
Вы использовали калькулятор много раз.
И вы знаете из чего он состоит.

Здесь есть клавиши с цифрами, которые помогут вам составить число.
Составленные числа отображаются на дисплее.
И тогда вы можете выполнять операции с этими числами,
Для которых вы используете другие клавиши, которые представляют эти операции.
Мы начнем с рассмотрения базового калькулятора.
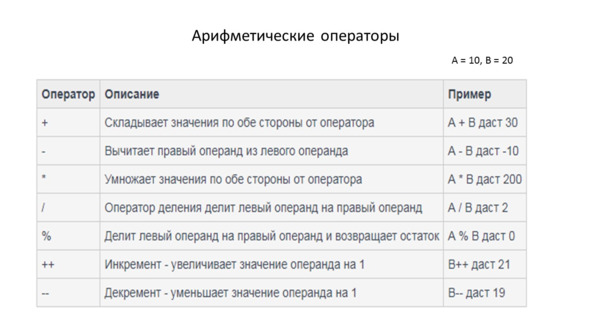
Таким образом, эти операции могут быть сложение, вычитание, умножение, и деление.
И калькулятор состоит из трех основных частей – дисплея, контрольной части, где есть завершающая вычисления клавиша равно и клавиша сброса, и клавиатура с цифрами и операциями.
Теперь, используя цифры, вы можете писать выражения и запрашивать их вычисления.
Выражение содержит числа и арифметические операции.
Эти выражения называются числовыми выражениями.
Теперь давайте улучшим этот калькулятор.
Но сначала давайте поговорим о выражениях.
Как правило, мы думаем о выражениях математически.
Это выражение равно другому выражению или какому-либо значению.
И это очень хорошая абстракция в большинстве случаев.
Но на самом деле мы знаем, что вычисление выражения требует усилий и времени.
И если у нас есть более сложное выражение, в нем может быть порядок, согласно которому вычисляются разные части этого выражения.
И вычисление более сложного выражения может занять больше времени.
Но что более важно, представьте, что у нас есть сложное выражение, и мы вычислили его один раз.
И мы должны снова вычислить его, если мы хотим позже получить значение выражения.
Хотя было бы неплохо иметь некий способ запомнить значение выражения для будущего использования?
Поэтому, рассмотрим такой калькулятор, где у нас есть запоминание.
Здесь у нас есть несколько клавиш для хранения или получения значений из этой памяти.
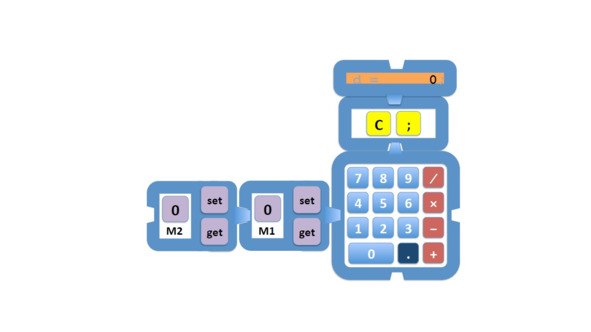
Функция запоминания позволяет нам сохранить значение для будущего использования.
Память может содержать значение, и могут быть связанные с ней операции, такие как MS, чтобы сохранить значение, и MR, чтобы восстановить его или вызвать его.
Иногда есть третья клавиша, MC для очистки памяти,
Назовем эти две клавиши для работы с памятью set и get.
Сейчас ячейки памяти названы предопределенными именами, M1, M2 и т. д.
Но мы хотели бы назвать их x и y, как мы привыкли в математике.
И мы будем присваивать этим ячейкам памяти имена переменных.

Теперь мы обсудим, что такое начальное значение переменной, которое сохраняется до того, как мы установим переменную в другое значение.
Мы можем сказать, что значение переменной неопределенно.
Поэтому, если мы попытаемся получить это значение, мы получим ошибку.
В калькуляторах, где есть числовые переменные, эта переменная обычно устанавливается равной 0, чтобы избежать ошибки.
Теперь мы хотим, чтобы дисплей показывал что-то, когда мы нажимаем кнопки Set или Get.
Давайте сначала поговорим о Set.
Предположим, что дисплей показывает число 3, и что мы нажимаем кнопку set переменной x.
Теперь значение 3 будет храниться в переменной x.

И дисплей может показать что-то вроде x равно 3 точка с запятой,
Чтобы записать то, что мы только что сделали.
Мы говорим, что мы назначили значение 3 переменной X, и записали это как x равно 3 в инструкции присваивания.
Как только мы установили значение переменной, мы можем использовать это значение в выражениях.
Например, представьте, что у нас есть 5 на дисплее,
И мы хотим добавить значение x.
Мы нажимаем символ плюса, а затем кнопку Get х.
Таким образом, мы увидим на дисплее 5 плюс x.

Но это выражение, и до того, как мы используем оператор присваивания, что дисплей действительно отображает, выражение или законченную операцию?
Мы можем рассматривать выражения в калькуляторе как законченные операции, считая, что дисплей также может считаться переменной, переменной с прямым вводом.
Поэтому на дисплее написано d равно перед выражением.
Таким образом мы преобразуем выражение в операцию.
На слайде показаны различные выражения присваивания.

Здесь показано, что выражения могут также иметь переменные.
И для вычисления выражения, нам нужно найти сохраненное значение в соответствующих переменных.
Теперь может оказаться, что одна и та же переменная появляется как слева, так и справа от присваивания.
Давайте проанализируем это более подробно.
Но сначала, давайте вспомним, что выражение присваивания состоит из переменной, за которой следует символ равенства, за которым следует выражение для вычисления, которое завершается точкой с запятой.
Представьте, что мы имеем три переменные x, y и z.
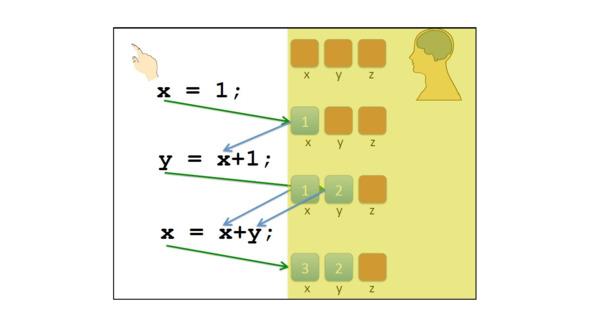
Мы не знаем их начальных значений.
У нас есть первая операция, которая присваивает 1 переменной x.
Поэтому после выполнения содержимое переменной x равно 1.
Следующая операция присваивания y равно x плюс 1.
Сначала мы должны оценить выражение справа, x плюс 1.
Для этого нам нужно получить значение, сохраненное в x.
Поэтому мы получаем 2 и 2 сохраняем в y.
Мы всегда работаем справа налево.
Сначала вычисляем выражение, а затем сохраняем результат в переменной.
Теперь мы сначала получаем значения x и y, складываем их вместе, получаем 3 и сохраняем 3 в x.
Переменные вместе со значениями – это то, что мы называем состоянием.
Таким образом, оператор присваивания преобразует одно состояние в другое состояние.
Здесь состояния обозначены фигурными скобками.
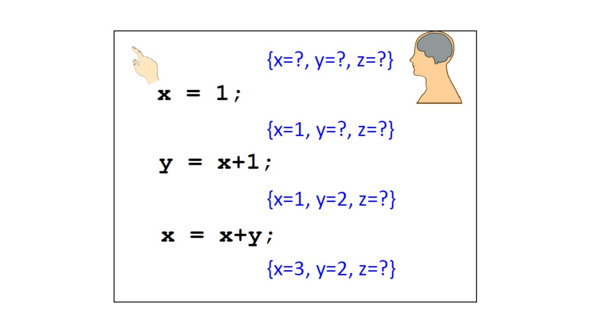
Коллекция значений переменных – это состояние.
Поэтому присваивание приводит к изменению состояния.
Теперь представьте, что вы сегодня делаете расчеты, и вы хотите повторить те же самые вычисления завтра.
Для этого вам нужно будет ввести все выражения снова.
Поэтому мы хотели бы иметь возможность записывать вычисления.
Точно так же, как мы хотим использовать память переменных для хранения значений, мы хотели бы теперь сохранить всю программу.
Некоторые калькуляторы печатают вычисления на бумаге.
Таким образом, у нас может быть запись наших вычислений.
Мы называем эту запись программой.
На данный момент программа является последовательностью простых вычислений.
Теперь было бы здорово, если бы мы могли повторно использовать программу, чтобы программа была не только результатом записи калькулятора, чтобы мы имели возможность подавать эту программу в калькулятор, как инструкции для повторного расчета.
Теперь наш калькулятор становится все больше похож на компьютер.
Таким образом, последовательность инструкций является программой.
Этот набор инструкций должен быть четко определен, и каждая из инструкций должна эффективно исполняться нашим компьютером.
Теперь эти инструкции обычно представляют собой текст.
Расширенный калькулятор выглядит следующим образом.

На дисплее теперь отображается история операций.
Это то, что мы называем программой.
Помимо записи истории операций, мы также хотим возможность ввода этой истории в калькулятор.
Таким образом, мы получим простой компьютер.
В общем и целом, программа является не чем иным, как записанным вычислением.
Ее можно записать на листе бумаги или сохранить другим способом, например, в памяти компьютера.
И компьютер будет интерпретировать эту программу и выполнять вычисление каждый раз, когда это потребуется.
Таким образом, мы прошли путь от значения и выражения до программы.

Основные операторы

Калькулятор, которые мы рассматривали, работал с числами.
Мы использовали числа и операции с числами для получения чисел.
Теперь, что делать, если вы хотите сравнить два числа?
Если мы хотим проверить, например, 5 меньше 6 или нет.
Ответ может быть положительным или отрицательным, – да или нет.
Это будет утверждение истинное или ложное.
В этом случае true и false также являются значениями, но они не являются числовыми значениями.
Их называют булевыми значениями в честь математика Джорджа Була.
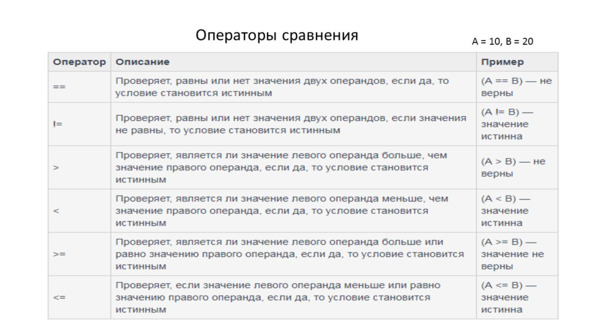
Существует шесть операций сравнения – меньше чем, больше чем, меньше или равно, больше или равно.

И наконец, мы должны проверить, являются ли два значения равными или разными.
Результатом проверки будет булево значение true или false.
Булевы значения представляют собой тип данных с двумя значениями true и false.
Мы могли бы назвать их да или нет, или один и ноль, но мы будем называть их true и false, как это делает Java.
И так же, как у нас были арифметические операции, теперь мы имеем несколько булевых операций.
Давайте посмотрим на некоторые из них.

Отрицание, которое также называется «нет» и представлено восклицательным знаком.
Эта операция принимает одно логическое значение, один аргумент, и возвращает другое логическое значение.
Конъюнкция – это еще одна операция, также называемая «и», и она представлена двумя амперсандами.
Эта операция принимает два значения, два аргумента.
И еще одна операция – дизъюнкция, также называемая «или», и она представлена двумя вертикальными полосами.
Эта операция также принимает два аргумента.
Операция отрицания принимает одно логическое значение и возвращает также логическое значение, а именно другое.
Таким образом, отрицание true, это false и наоборот.
Операция «и» принимает два boolean значения в качестве аргумента и возвращает boolean значение.
И результат true, если оба аргумента true, и false в противном случае.
Операция или также принимает два аргумента, два булевых значения и возвращает булево значение.
Теперь результат true, если какой-либо аргумент true, и false, если оба аргумента являются false.
Мы могли бы добавить все эти операции в наш калькулятор, который бы исполнял их также успешно, как и операции с числами.
Таким образом, суммируя, в Java мы имеем следующие основные операторы.
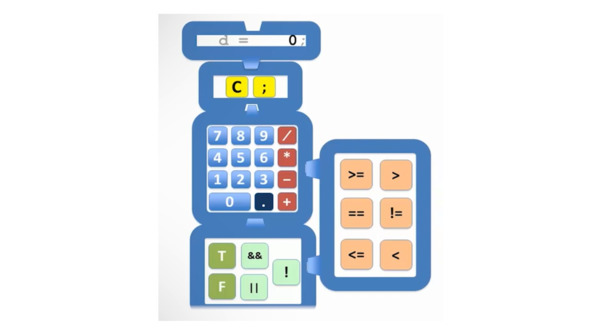
А также оператор присваивания = равно.

Переменные
Теперь, когда мы добавляли переменные в калькулятор, мы хотели называть их своими именами.
В Java, когда мы хотим использовать переменную, мы должны сначала представить ее с помощью объявления.
Объявление должно включать сначала тип данных переменной.

В Java существует несколько типов данных, предусмотренных для чисел.
На данный момент для упрощения, представьте себе, что у нас есть один тип данных, называемый «int».
«int» включает в себя как положительные, так и отрицательные целые числа, в некоторых пределах.

Таким образом, объявление переменной состоит из имени типа, затем имени переменной и точки с запятой.



