
Полная версия:
Высшая математика. Шпаргалка

Высшая математика. Шпаргалка
1. Основные понятия. Системы координат. Прямые линии и их взаимное расположение
Координата точки – это величина, определяющая положение данной точки на плоскости, на прямой или кривой линии или в пространстве. Значение координаты зависит от выбора начальной точки, от выбора положительного направления и от выбора единицы масштаба.
Прямоугольная система координат состоит из двух взаимно перпендикулярных прямых – осей, точка их пересечения – начало координат О, ось ОХ – ось абсцисс, ось ОY – ось ординат. На осях выбираются масштаб и положительное направление.
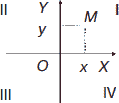
Рис. 1
Системы координат
Положение точки М определяется двумя координатами: абсциссой х и ординатой у. Записывается так: М(х, у). Оси координат образуют четыре координатных угла I, II, III, IV. Если точка находится в I координатном угле (квадранте), то и абсцисса, и ордината ее положительные, если – во II квадранте, то абсцисса отрицательна, а ордината положительна, если в – III квадранте, и абсцисса, и ордината отрицательны, если – в IV квадранте, положительна абсцисса, а ордината отрицательна. У точки, лежащей на оси ординат, абсцисса равна нулю, и наоборот, если точка лежит на оси абсцисс, то ее ордината равна нулю.
Косоугольной системой координат аналогична прямоугольной, только оси координат пересекаются под углом не равным прямому. Прямоугольная и косоугольная системы относятся к декартовой системе координат.
Полярная система координат состоит из полюса О и полярной оси ОХ, проведенной из полюса. Положение точки определяется полярным радиусом ρ (отрезок ОМ) и полярным углом φ. Для полярного угла берется его главное значение (от –π до π). Числа ρ, φ называются полярными координатами точки М.
Связь между координатами точки в прямоугольной и полярной системах координат: x = r cosφ, y = r sinφ или:
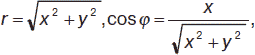
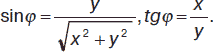
Пусть имеются две точки М1(х1, у1) и М2(х2, у2). Расстояние между точками:
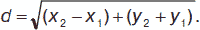
Общее уравнение прямой линии (система координат прямоугольная): Ах + Ву + С = 0 (А и В одновременно не равны нулю).
Если В не равно нулю, то уравнение прямой: у = ах + b (здесь а = – А / В, b = – С / В). Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат. Уравнение прямой, параллельной оси абсцисс: у = b, уравнение оси абсцисс: у = 0; уравнение прямой, параллельной оси ординат: х = с, уравнение оси ординат: х = 0.
2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых. Расстояние от точки до прямой
1. Пусть даны три точки А1 (х1, у1), А2 (х2, у2), А3 (х3, у3), тогда условие нахождения их на одной прямой:
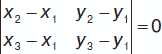
либо (х2 – х1) (у3 – у1) – (х3 – x1) (у2 – у1) = 0.
2. Пусть даны две точки А1 (х1, у1), А2 (х2, у2), тогда уравнение прямой, проходящей через эти две точки:
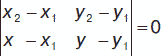
(х2 – х1)(у – у1) – (х – х1)(у2 – у1) = 0 или (х – х1) / (х2 – х1) = (у – у1) / (у2 – у1).
3. Пусть имеются точка М (х1, у1) и некоторая прямая L, представленная уравнением у = ах + с. Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:
у – у1 = а(х – х1).
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М, описывается уравнением А(х – х1) + В(у – у1) = 0.
Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М:
у – у1 = –(х – х1) / а
или
а(у – у1) = х1 – х.
Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М(х1, у1), описывается уравнением А (у – у1) – В(х – х1) = 0.
4. Пусть даны две точки А1 (х1, у1), А2 (х2, у2) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:
1) точки А1, А2 лежат по одну сторону от данной прямой, если выражения (Ах1 + Ву1 + С) и (Ах2 + Ву2 + С) имеют одинаковые знаки;
2) точки А1, А2 лежат по разные стороны от данной прямой, если выражения (Ах1 + Ву1 + С) и (Ах2 + Ву2 + С) имеют разные знаки;
3) одна или обе точки А1, А2 лежат на данной прямой, если одно или оба выражения соответственно (Ах1 + + Ву1 + С) и (Ах2 + Ву2 + С) принимают нулевое значение.
5. Центральный пучок – это множество прямых, проходящих через одну точку М (х1, у1), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у – у1 = к (х – х1) (параметр пучка к для каждой прямой свой).
Все прямые пучка можно представить уравнением: l(y – y1) = m(x – x1), где l, m – не равные одновременно нулю произвольные числа.
Если две прямые пучка L1 и L2 соответственно имеют вид (А1х + В1у + С1) = 0 и (А2х + В2у + С2) = 0, то уравнение пучка: m1(А1х + В1у + С1) + m2(А2х + В2у + С2) = 0. Если прямые L1 и L2 пересекающиеся, то пучок центральный, если прямые параллельны, то и пучок параллельный.
6. Пусть даны точка М (х1, у1) и прямая, заданная уравнением Ах + Ву + С = 0. Расстояние d от этой точки М до прямой:
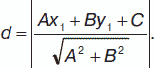
3. Полярные параметры прямой. Нормальное уравнение прямой. Преобразование координат
Полярными параметрами прямой L будут полярное расстояние р (длина перпендикуляра, проведенного к данной прямой из начала координат) и полярный угол α (угол между осью абсцисс ОХ и перпендикуляром, опущенным из начала координат на данную прямую L). Для прямой, представленной уравнением Ах + Ву + С = 0: полярное расстояние
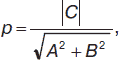
полярный угол α
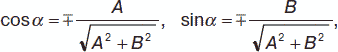
причем при C > 0 берется верхний знак, при C < 0 – нижний знак, при С = 0 знаки берутся произвольно, но либо оба плюса, либо оба минуса.
Нормальное уравнение прямой (уравнение в полярных параметрах) (cм. рис. 2): x cosα + y sinα – p = 0. Пусть прямая представлена уравнением вида Ах + Ву + С = 0. Чтобы данное уравнение привести к нормальному виду необходимо последнее разделить на выражение

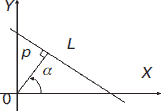
Рис. 2
После деления получается нормальное уравнение данной прямой:
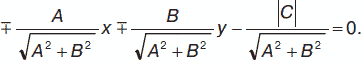
Пусть имеется прямая L, которая пересекает оси координат. Тогда данная прямая может быть представлена уравнением в отрезках х / а + у / b = 1. Справедливо: если прямая представлена уравнением х / а + у / b = 1, то она отсекает на осях отрезки а, b.
Преобразование координат возможно путем переноса начала координат, или поворотом осей координат, или совместно переносом начала и поворотом осей.
При переносе начала координат справедливо следующее правило: старая координата точки равна новой, сложенной с координатой нового начала в старой системе. Например, если старые координаты точки М были х, у, а координаты нового начала в старой системе О*(х0, у0), то координаты точки М в новой системе координат с началом в точке О* будут равны х – х0, у – у0 т. е. справедливо следующее х = х* + х0, у = у* + у0 или х* = х – х0, у* = у – у0 (* новые координаты точки).
При повороте осей на некоторый угол φ справедливы следующие формулы (где х, у – старые координаты точки; х*, у* – новые координаты этой же точки):
x = x* cosα – y* sinα;
y = x* sinα + y* cosα
или
x* = x cosα + y sinα;
y* = – x sinα + y cosα.
4. Порядок алгебраических линий. Окружность. Эллипс. Гипербола. Парабола
Линия L, представленная в декартовой системе уравнением n–степени называется алгебраической линией n–порядка.
Окружность с радиусом R и центром в начале координат описывается уравнением: х2 + у2 = R2, если центром окружности является некоторая точка С (а, b), то уравнением:
(х – а)2 + (у – b)2 = R2.
Чтобы уравнение Ах2 + Вх + Ау2 + Су + D = 0 описывало окружность, необходимо, чтобы оно не содержало члена с произведением ху, чтобы коэффициенты при х2 и у2 были равны, чтобы В2 + С2 – 4АD > 0 (при невыполнении данного неравенства уравнение не представляет никакой линии).
Координаты центра окружности, описанной уравнением Ах2 + Вх + Ау2 + Су + D = 0 и ее радиус: a = –B / 2A, b = –C / 2A, R2 = (В2 + С2 – 4АD) / 4A2.
Эллипс – сжатая окружность (рис. 3).
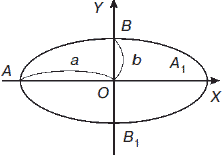
Рис. 3
Прямая АА1 называется осью сжатия, отрезок АА1 = 2а – большой осью эллипса, отрезок ВВ1 = 2b – малой осью эллипса (a > b) точка О – центром эллипса, точки А, А1, В, В1 – вершинами эллипса. Отношение k = b / a коэффициент сжатия величина α = 1 – k = (a – b) / a – сжатие эллипса. Эллипс обладает симметрией относительно большой и малой осей и относительно своего центра.
Каноническое уравнение эллипса: x2 / a2 + y2 / b2 = 1.
Другое определение эллипса: эллипс есть геометрическое место точек (М), сумма расстояний которых до двух данных точек F, F1 имеет одно и то же значение 2а (F1M + FM = 2a) (рис. 4).
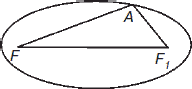
Рис. 4
Точки F и F1 называются фокусами эллипса, а отрезок FF1 – фокусным расстоянием, обозначается FF1 = 2с, причем с < а. Эксцентриситет эллипса ε – это отношение фокусного расстояния к большой оси ε = с / а. Эксцентриситет эллипса меньше единицы, имеем: k2 = 1 – ε2.
Гипербола – это геометрическое место точек, разность расстояний которых до двух данных точек F, F1 имеет одно и то же абсолютное значение (рис. 5). |F1M – FM| = 2a. Точки F, F1 называются фокусами гиперболы, расстояние FF1 = 2c – фокусным расстоянием. Справедливо: c > a.
Каноническое уравнение гиперболы: х2 / а2 + у2 / (а2 – с2) = 1. Асимптоты гиперболы заданы уравнениями у = bx / a и y = – bx / a (b2 = c2 – a2).
Парабола – это геометрическое место точек равноудаленных от данной точки F (фокуса параболы) и данной прямой PQ (директрисы параболы). Расстояние от фокуса до директрисы FC называется параметром параболы и обозначается р. Вершина параболы – точка О. Каноническое уравнение параболы: у2 = 2рх.
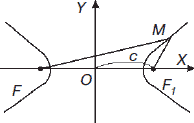
Рис. 5
5. Аналитическая геометрия в пространстве. Плоскость
Всякая поверхность в пространстве определяется уравнением вида f(x, y, z) = 0.
Общее уравнение плоскости: Ах + Ву + Сz + D = 0. Если А, В, С, D не равны нулю, то уравнение называется полным.
При D = 0 уравнение Ах + Ву + Сz = 0 определяет плоскость, проходящую через начало координат.
Если А = 0, то уравнение определяет плоскость, параллельную оси Ох. Если два из коэффициентов А, В, С равны нулю одновременно, то уравнение определяет плоскость, параллельную одной из координатных плоскостей: при А = 0 и В = 0 параллельно плоскости хОу, при А = 0 и С = 0 параллельно хОz, при В = 0 и С = 0 параллельно yOz. Уравнение Cz = 0 определяет плоскость xOy, By = 0 – плоскость xOz, Ax = 0 – плоскость yOz. Уравнение плоскости в «отрезках»: х / а + у / b + z / c = 1. Расстояние от точки М (х1, у1, z1) до плоскости:
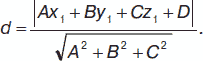
Пусть имеются две плоскости А1х + В1у + С1z + D1 = 0 и А2х + В2у + С2z + D2 = 0. Угол φ между этими плоскостями:
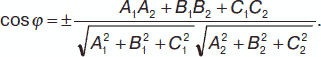
Условие равенства двух плоскостей: А1 / А2 = В1 / В2 = С1 / С2 = D1 / D2. Условие параллельности плоскостей: А1 / А2 = В1 / В2 = С1 / С2. Условие перпендикулярности плоскостей: А1А2 + В1В2 + С1С2 = 0. Уравнение плоскости, проходящей через заданную точку М (х1, у1, z1) параллельно плоскости, заданной уравнением Ах + Ву + Сz + D = 0: А(х – x1) + В(у – y1) + С(z – z1) + D = 0. Уравнение плоскости, проходящей через три точки М1 (х1, у1, z1), М2 (х2, у2, z2), М3 (х3, у3, z3):
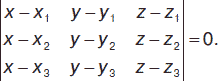
Уравнение плоскости, проходящей через две точки М1(х1, у1, z1) и М2(х2, у2, z2) перпендикулярно к плоскости, заданной уравнением Ax + By + Cz + D = 0:
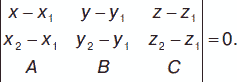
Уравнение плоскости, проходящей через точку М1 (х1, у1, z1) перпендикулярно двум непараллельным плоскостям А1х + В1у + С1z + D1 = 0 и А2х + В2у + С2z + D2 = 0, имеет вид:
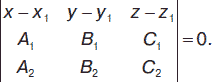
Имеем три плоскости, заданные общими уравнениями:
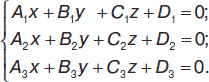
6. Прямая в пространстве
Всякая прямая определяется в пространстве системой двух уравнений
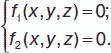
Канонические (симметричные) уравнения прямой: (x – x0) / m = (y – y0) / p = (z – z0) / q, прямая проходит через точку M0 (x0, y0, z0). Угол φ между двумя прямыми, заданными каноническими уравнениями:
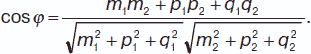
Условие параллельности двух прямых: m1 / m2 = p1 / p2 = q1 / q2. Условие перпендикулярности двух прямых: m1m2 + p1p2 + q1q2 = 0.
Пусть имеются прямая (x – x0) / m = (y – y0) / p = (z – z0) / q и плоскость Ах + Ву + Сz + D = 0. Условие параллельности прямой и плоскости: Am + Bp + Cq = 0. Условие перпендикулярности прямой и плоскости: A / m = B / p = C / q. Условие принадлежности прямой плоскости:
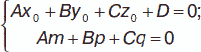
Если прямая задана параметрически x
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Полная версия книги
Всего 10 форматов



