
Полная версия:
Экономический анализ

Наталия Владимировна Климова
Экономический анализ
Предисловие
Предлагаемое читателям учебное пособие поможет освоить теоретические основы экономического анализа хозяйственной деятельности в сочетании с производственным (управленческим) и финансовым анализом.
Экономический анализ рассматривается как научная дисциплина, предназначенная для:
• понимания сущности экономических явлений и процессов, их взаимосвязи и взаимозависимости;
• систематизации и моделирования факторных моделей;
• определения влияния факторов на результаты деятельности организации;
• выявления и подсчета экономических резервов развития бизнеса;
• овладения навыками организации аналитической работы на предприятии и повышения научно-экономической обоснованности бизнес-планов.
Изучение экономического анализа способствует формированию компетентностно-квалификационной характеристики выпускника.
Данное учебное пособие соответствует Государственному образовательному стандарту специальности 060400 «Финансы и кредит» и 060500 – «Бухгалтерский учет, анализ и аудит».
Вопрос 1
Предмет, объект и содержание экономического анализа
Термин «анализ» происходит от греческого слова analysis «разложение, расчленение».
Экономический анализ представляет собой способ познания предметов и явлений окружающей среды, основанный на расчленении целого на составные части и изучении их во всем многообразии связей и зависимостей. Например, чтобы понять сущность себестоимости продукции, необходимо знать не только какие статьи затрат в нее включены, но и от каких факторов зависит величина каждого вида расходов.
Экономический анализ раскрывается через такие понятия, как теория познания, суждение, умозаключение, научная абстракция, мышление.
Теория познания определяет сущность, необходимость и последовательность экономического анализа. Объектом познания являются практика и человеческое мышление. Мышление в качестве творческого процесса включает суждение и умозаключение. Через суждение что-либо отрицается или утверждается. Суждение может быть от частного к общему (индукция) и наоборот от общего к частному (дедукция).
Индукция и дедукция неразрывно связаны друг с другом и в совокупности представляют умозаключение. Индуктивно-дедуктивный способ мышления, прошедший логическую обработку объективных данных, раскрывает сущность изучаемых экономических явлений, позволяет выявить определенные закономерности и принять грамотные управленческие решения.
Под предметом экономического анализа понимают:
• хозяйственные процессы предприятий, социально-экономическую эффективность и конечные финансовые результаты их деятельности, складывающиеся под воздействием объективных и субъективных факторов, получающие отражение через систему экономической информации;
• причинно-следственные связи экономических явлений и процессов, т. е. причины изменений, познание которых позволяет определить сущность экономических явлений и на этой основе дать правильную оценку и обоснование любого управленческого решения.
В последние время большинство научных исследователей предметом экономического анализа считают хозяйственные процессы организаций, включающие организационно-производственную, коммерческую, финансовую, социальную, техническую и технологическую сферы деятельности.
Объектами анализа являются результаты экономических процессов. Это показатели источников и средств основного и оборотного капитала, инвестиционной и инновационной деятельности, эффективности использования ресурсов предприятия, объема производства, продаж, прибыли и рентабельности. Например, в любой сфере деятельности к объектам анализа относятся производство и продажа продукции, оказание работ и услуг, их себестоимость, финансовые результаты, степень использования различных видов ресурсов (фондоотдача, материалоемкость, производительность труда и др.).
Вопрос 2
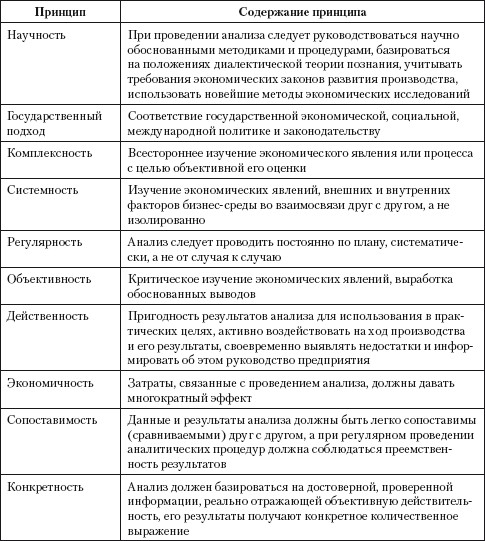
Принципы экономического анализа
Экономический анализ, как и любая наука, имеет принципы, или требования, которым она должна соответствовать.
Вопрос 3
Цель и задачи экономического анализа
Цель экономического анализа финансово-хозяйственной деятельности организаций заключается в поиске и измерении резервов повышения эффективности производства, роста конкурентоспособности и финансовой устойчивости. Задачи экономического анализа:
• установление закономерностей и тенденций экономических явлений и процессов в конкретных условиях предприятия. Например, закон опережающего роста производительности труда относительно уровня его оплаты должен выполняться не только в масштабах всей национальной экономики, но и на каждом конкретном предприятии и в его подразделениях;
• научное обоснование перспективных планов и прогнозов. Без глубокого экономического анализа результатов деятельности предприятия за прошедшие 5-10 лет, без выявления имевших место недостатков и преимуществ нельзя разработать обоснованный план, выбрать оптимальный вариант управленческого решения;
• разграничение субъективных и объективных причин отклонения фактических показателей от базисных и количественное их измерение;
• оценка результатов деятельности фирмы по выполнению планов, достигнутому уровню развития экономики, использованию имеющихся ресурсов и потенциала организации, выбор оптимального управленческого решения;
• прогнозирование показателей на перспективу и разработка мероприятий по использованию выявленных резервов;
• контроль за внедрением разработанных мероприятий, выполнением уровня плановых показателей и экономным использованием ресурсов.
Вопрос 4
Классификация видов экономического анализа
Виды экономического анализа классифицируют:
• по содержанию и полноте изучаемых объектов (комплексный анализ всей хозяйственной деятельности, локальный анализ отдельных подразделений, тематический анализ отдельных вопросов). При комплексном анализе деятельность предприятия изучается всесторонне, а при тематическом – только отдельные ее стороны, представляющие в определенный момент наибольший интерес;
• по методам, изучения объектов (сравнительный, факторный, маржинальный, экономико-математический, стохастический, функционально-стоимостной, диагностический анализ (экспресс-анализ)).
♦ Сравнительный анализ ограничивается сравнением отчетных показателей – результатов хозяйственной деятельности с показателями плана текущего года, прошлых лет и данными конкурентов.
♦ Факторный анализ направлен на выявление количественной величины влияния факторов на прирост и уровень результативных показателей.
♦ Маржинальный анализ – это метод оценки и обоснования эффективности управленческих решений в бизнесе на основании причинно-следственной взаимосвязи объема продаж, себестоимости и прибыли и деления затрат на постоянные и переменные.
♦ Диагностический анализ представляет собой способ установления тенденций изменений экономических процессов на основе характерных для них типичных признаков. К примеру, если темпы роста валовой продукции опережают темпы роста товарной продукции, то это свидетельствует о росте остатков незавершенного производства. Если темпы роста валовой продукции выше темпов роста производительности труда, то это признак невыполнения плана мероприятий по механизации и автоматизации производства, улучшению организации труда и на этой основе сокращение численности работников;
• по периодичности (годовой, квартальный, декадный, разовый, ежедневный);
• по признаку времени (ретроспективный и перспективный).
♦ Перспективный (предварительный) анализ проводится до осуществления хозяйственных операций. Он необходим для обоснования управленческих решений и прогнозируемых показателей, а также для контроля за выполнением плана и предупреждения нежелательных результатов. Перспективный анализ широко используется при разработке бизнес-планов и обосновании инвестиционных проектов.
♦ Ретроспективный (последующий, исторический) анализ проводится после совершения хозяйственных актов. Он используется для контроля за выполнением программ развития фирм в динамике лет, выявления неиспользованных резервов, объективной оценки результатов деятельности организаций. Недостаток анализа заключается в том, что выявленные резервы означают навсегда потерянные возможности роста эффективности производства, поскольку относятся к прошлому периоду. Ретроспективный анализ является основой перспективного анализа. В свою очередь, от глубины и качества предварительного анализа на перспективу зависят результаты последующего анализа. Ретроспективный анализ подразделяется на оперативный и текущий. Оперативный (ситуационный) анализ проводится сразу после совершения хозяйственных операций или изменения ситуации за короткие отрезки времени (смену, декаду, сутки и т. д.). Его цель оперативно выявлять недостатки и воздействовать на хозяйственные процессы. Он широко используется, например, при анализе уровня выполнения плана розничного и оптового товарооборота за день, ритмичности производства, ассортимента и качества продукции, движения денежных потоков, обеспеченности материалами, использования рабочего времени.
Отличительная черта оперативного анализа – исследование преимущественно натуральных показателей, его неточность, связанная с приближенностью в расчетах. Текущий анализ проводится по важным отчетным периодам хозяйствования в основном на базе периодической, годовой бухгалтерской отчетности. Главная задача текущего анализа объективная оценка результатов коммерческой деятельности, комплексное выявление недочетов в работе, неиспользованных резервов и мобилизации их для повышения экономической эффективности производства, улучшения финансового положения в долгосрочной перспективе. Текущий анализ является наиболее полным, аккумулирующим результаты оперативного анализа и служащим базой перспективного анализа. Он рекомендуется для проведения комплексного выявления и измерения причинно-следственных взаимосвязей в использовании ресурсов предприятия;
• по объектам управления (технико-экономический анализ, финансово-экономический, аудиторский, социально-экономический, экономико-экологический и маркетинговый анализ).
♦ Технике-экономическим анализом занимаются технические службы предприятия. Его содержанием является изучение взаимодействия технических, технологических и экономических процессов и установление их влияния на экономические результаты деятельности фирмы. Пример использование энергосберегающих технологий производства.
♦ В финансово-экономическом анализе основное внимание уделяется финансовым результатам деятельности предприятия, эффективности использования заемного и собственного капитала, выявлению резервов увеличения суммы прибыли, роста рентабельности, платежеспособности.
♦ Социально-экономический анализ изучает взаимосвязь социальных и экономических процессов, их влияние друг на друга.
♦ Экономико-статистический анализ применяется для изучения массовых общественных явлений на разных уровнях управления: предприятия, отрасли, региона.
♦ Экономико-экологический анализ исследует взаимодействие экономических и экологических процессов, связанных с сохранением и улучшением окружающей среды и затратами на экологию.
♦ Маркетинговый анализ применяется для изучения внешней среды функционирования предприятия, рынка сырья и сбыта готовой продукции, ее конкурентоспособности, спроса и предложения, коммерческого риска и т. п.
♦ Управленческий анализ более подробный и затрагивает все сферы деятельности предприятия, данные первичного и оперативного учета. В то же время информация, подвергаемая управленческому анализу, представляет коммерческую тайну и результаты анализа используются только для внутрихозяйственного управления.
♦ Финансовый анализ менее надежен в точности оценки финансового состояния, так как многие показатели бухгалтерской официальной отчетности искажают в целях сокрытия прибыли и механизма ее получения.
Каждый из перечисленных видов экономического анализа различен по содержанию, организации и методике его проведения. В практической деятельности используются одновременно несколько видов анализа, представляющие единую систему принятия эффективных управленческих решений.
Вопрос 5
Метод экономического анализа, его характерные особенности и классификация
Метод экономического анализа представляет системное комплексное изучение, выявление, измерение и обобщение влияния факторов на результаты деятельности организации путем обработки системы показателей специальными приемами. Он состоит из ряда последовательно осуществляемых действий:
• наблюдение за объектом, расчет абсолютных и относительных показателей, приведение их в сопоставимый вид;
• систематизация, группировка и детализация факторов, изучение их влияния на результативные показатели;
• обобщение построение итоговых и прогнозных таблиц, подготовка выводов и рекомендаций для принятия управленческих решений.
Характерные черты метода следующие.
• Необходимость постоянных сравнений.
• Необходимость изучения внутренних противоречий, положительных и отрицательных сторон каждого явления, каждого процесса. Например, научно-технический прогресс (НТП) оказывает положительное влияние на рост производительности труда, наращивание прибыли и повышение уровня рентабельности, но при этом может иметь место загрязнение окружающей среды.
• Системность и комплексность проведения экономического анализа; изучение хозяйственной деятельности предприятий проводится с учетом всех взаимосвязей и взаимозависимостей. Так, с внедрением новой техники увеличиваются издержки производства, но при этом возрастает производительность труда, что, в свою очередь, способствует экономии заработной платы. И если темпы роста производительности труда будут превышать темпы роста издержек на содержание и эксплуатацию новой техники, то управленческое решение экономически обоснованно и правомерно.
• Установление причинно-следственных связей, т. е. выявление причин изменений экономических показателей и прогноз возможных тенденций.
• Определение количественного влияния факторов на результативные показатели деятельности фирмы, расчет экономических потерь и резервов предприятия.
Классификация методов экономического анализа следующая: Неформализованные методы основаны на отражении аналитических процедур на логическом уровне, а не на строгих аналитических зависимостях. К ним относятся: разработка системы показателей, метод сравнений, построение аналитических таблиц, прием детализации, метод экспертных оценок, методы ситуационного анализа и прогнозирования.
К формализованным относятся методы, которые позволяют представить показатели в строгой зависимости (преимущественно математической). Среди них выделяют:
• классические методы экономического анализа (балансовый способ, методы детерминированного факторного анализа (цепных подстановок, абсолютных и относительных разниц), интегральный и логарифмический методы);
• традиционные методы экономической статистики (метод средних величин, метод группировок, индексный метод);
• математико-статистические методы изучения связей (корреляционный, регрессионный, дисперсионный, кластерный анализ);
• методы финансовых вычислений;
• методы теории принятия решений (метод построения дерева решений, линейное программирование и анализ чувствительности).
Вопрос 6
Методы в экономическом факторном анализе
Классификация методов экономического анализа представлена на рис. 1.
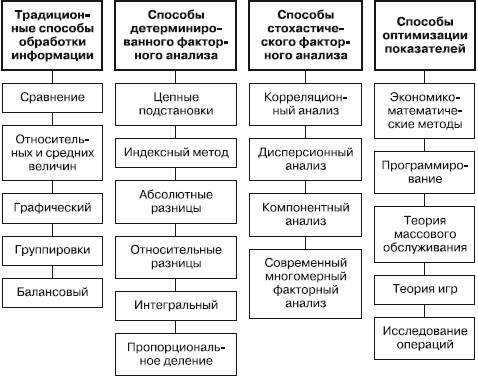
Рис. 1. Методы экономического анализа хозяйственно-финансовой деятельности и диагностики организации
Из статистических методов наиболее востребованы в экономическом анализе следующие способы детерминированного факторного анализа:
• индексный;
• цепной подстановки;
• исчисления абсолютных и относительных разниц;
• интегральный;
• логарифмический метод;
• метод корреляционно-регрессионного анализа.
Основу способов детерминированного факторного анализа составляет метод элимирования.
Элимировагпъ значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменений, потом изменяются два, затем три и т. д. фактора при неизменности остальных.
Способ цепной подстановки позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных показателей, количество которых на единицу меньше, чем факторов.
Порядок применения этого способа лучше рассмотреть на конкретном примере: объем продаж (стоимость товарной продукции или выручка ТП) зависит от двух факторов первого уровня – количества проданной продукции (К) и цены реализации (Ц): ТП = К х Ц.
Алгоритм расчета:
1. Рассчитаем плановую (ТПпл) и фактическую (ТПф) выручку:
ТПпл =Кпл х Цпл;
ТПф = Кф х Цф.
2. Определим выручку условную (ТПусл):
ТПусл = Кф х Цпл.
3. Рассчитаем отклонение фактической выручки от плановой (ΔТПобщ).
ΔТПобщ = ТПф – ТПпл.
4. Рассчитаем изменение выручки за счет:
• изменения количества проданной продукции (ΔТПк):
ΔТПк = ТПусл – ТПпл
• изменения цены реализации (ΔТПц):
ΔТПц = ТПф – ТПусл.
5. Проверим правильность алгебраических расчетов: алгебраическая сумма влияния факторов должна быть равна общему приросту результативного показателя:
ТПусл + ΔТПц = ΔТПобщ.
Используя способ цепной подстановки, необходимо выполнить ряд правил:
• в первую очередь учитывается изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и качественных факторов, то сначала следует изменить факторы первого уровня подчинения, а потом второго;
• в расчетах количественного влияния факторов на результат обязательно используется условный показатель;
• фактические данные сравниваются с плановыми (или данные отчетного периода с базисными показателями).
Способ абсолютных разниц используется только в мультипликативных и смешанных моделях. При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на плановую (базовую) величину факторов, которые находятся справа от него, и на фактическую (отчетную) величину факторов, расположенных слева от него в модели.
Алгоритм, расчета:
1. Рассчитаем абсолютное изменение:
• объема реализации (ΔК):
ΔК = Кф – Кпл;
• цены (ΔЦ):
2. Рассчитаем изменение выручки за счет:
• изменения количества проданной продукции (ΔТПк):
ΔТПк = ΔК х Цпл;
• изменения цены реализации (ΔТПц):
ΔТПц = Кф х ΔЦ.
3. Проверка расчетов:
ΔТПк + ΔТПц = ΔТПобщ
Способ относительных разниц применяется в тех же моделях, что и при использовании метода абсолютных разниц. Он значительно проще цепных подстановок, что делает его более эффективным, особенно когда требуется рассчитать влияние более 8 факторов.
Алгоритм расчета:
1. Для расчета влияния первого фактора необходимо плановую (базисную) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100 %.
Изменение выручки за счет количества проданной продукции (ДТПк):
ΔТПк = (ТПпл х ΔК%)/100 %;
ΔК% = (Кф – Кпл)/Кпл х 100 %.
2. Чтобы рассчитать влияние второго фактора, необходимо к плановой величине результативного фактора прибавить изменение результативного показателя за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100 %.
Изменение выручки за счет цены реализации (ΔТПц):
ΔТПц = (ТПпл + ΔТПк) х ΔЦ%/100 %;
ΔЦ% = (Цф-Цпл)/Цплх100 %.
3. Влияние третьего, четвертого и т. д. факторов (при их наличии) определяется аналогично второму этапу с добавлением в сумму изменения результата за счет влияния второго, третьего и т. д. факторов.
4. Проверка расчетов:
ΔТПк + ΔТПц = ΔТПобщ
Недостаток предыдущих методов состоит в том, что научно-технические факторы интенсификации производства не могут быть включены в модель прямых связей, а следовательно, их недоучет приведет к занижению или завышению отдельных результатов.
Вторым недостатком является зависимость результатов расчетов от того, насколько логически и экономически правильно составлена формула и, следовательно, могут быть сформулированы различные выводы.
Поэтому, прежде чем приступить к расчетам, необходимо:
• выявить четкую взаимосвязь между изучаемыми показателями (явлениями);
• разграничить количественные и качественные показатели;
• правильно определить последовательность подстановок в тех случаях, когда имеется несколько количественных и качественных показателей.
Интегральный метод имеет преимущества, заключающиеся в получении более точных результатов расчета влияния факторов по сравнению с другими методами и исключения неоднородной оценки влияния факторов. Это является следствием того, что результаты расчетов не зависят от местоположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними пропорционально изолированному их воздействию на результативный показатель.
Интегральный метод применяется в мультипликативных, кратных и смешанных моделях с использованием для каждой из них определенных формул.
1. Для двухфакторных мультипликативных моделей.
Пример: ТП = К х Ц.
Расчет изменения выручки за счет:
• количества проданной продукции (ΔТПк):
ΔТПк =1/2К х (Цпл + Цф);
• цены реализации (ΔТПц):
ΔТПц =1/2Ц х (Кпл + Кф).
2. Для кратной двухфакторной модели: А = В/С.
ΔАобщ = Аф – Апл;
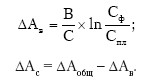
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. При логарифмировании используются не абсолютные приросты результативных показателей, а индексы их роста или снижения. Общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму индекса результативного показателя.
Способ пропорционального деления используется для аддитивных и кратно-аддитивных моделей.
Алгоритм расчета количественного влияния исследуемого фактора на изменение результативного показателя для аддитивной модели:
• абсолютное изменение результативного показателя делится на сумму абсолютных изменений всех факторов;
• полученный результат умножается на абсолютное отклонение исследуемого фактора.
Пример: Y = х1 + х2 + х3.
Изменение Yза счет фактора х1:
ΔYх1 = ΔYобщ /(Δх1 + Δх2 + Δх3) × Δх1.
Изменение Y за счет фактора х2:
ΔYх2 = ΔYобщ /(Δх1 + Δх2 + Δх3) × Δх2.
Изменение Y за счет факторах,
ΔYх3 = ΔYобщ /(Δх1 + Δх2 + Δх3) × Δх3.
Сумма влияния факторов должна быть равна общему изменению результативного показателя.
Метод корреляционно-регрессионного анализа позволяет определить изменение результативного показателя под воздействием одного или нескольких факторов, т. е. определить, на сколько единиц изменяется величина результативного показателя при изменение факторного на единицу, а также позволяет установить относительную степень зависимости результативного показателя от каждого фактора. Корреляционная зависимость проявляется лишь в среднем (как среднее значение) и только в массе наблюдений.
Множественная корреляционная модель имеет вид:
y = а0 + а1х1 + а2х2 + а3х3 + … + аnхn,



