
Полная версия:
The Great Arc: The Dramatic Tale of How India was Mapped and Everest was Named


THE GREAT ARC
The Dramatic Taleof how India was Mappedand Everest was Named
JOHN KEAY

Dedication
For Julia
Epigraph
Know …
That on the summit whither thou art bound
A geographic Labourer pitched his tent,
With books supplied and instruments of art,
To measure height and distance; lonely task,
Week after week pursued!
From ‘Written with a slate pencil on a stone
on the side of the mountain of Black Comb’,
WILLIAM WORDSWORTH, 1818
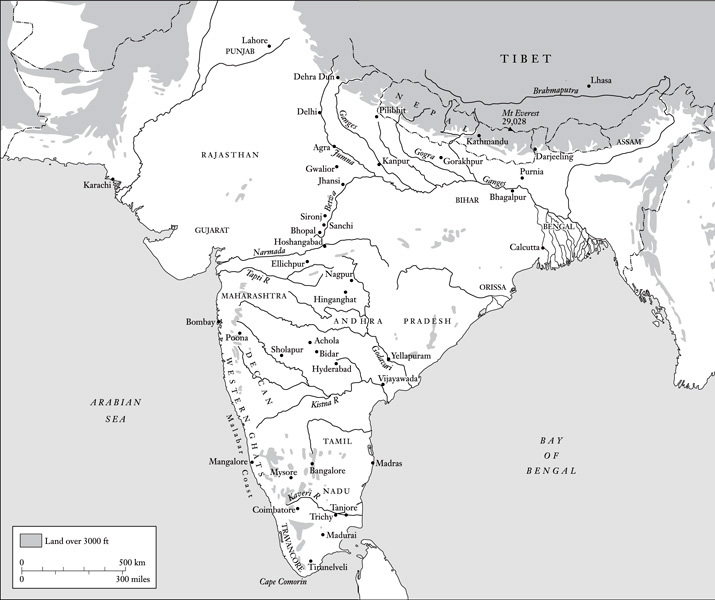
India
Contents
Cover
Title Page
Dedication
Epigraph
List of Maps
A Note on Spellings
Foreword
1 A Baptism of Fever
2 The Elusive Lambton
3 Tall Tales from the Hills
4 Droog Dependent
5 The Far-Famed Geodesist
6 Everywhere in Chains
7 Crossing the Rubicon
8 So Far as Our Knowledge Extends
9 Through the Haze of Hindustan
10 Et in Arcadia
11 A Stupendous Snowy Mass
A Note on Sources
Index
About the Author
Praise
By the Same Author
Copyright
About the Publisher
List of Maps
The Great Arc and Associated Series
General Map of India
The Himalayas
A Note on Spellings
Some proper names in the text, especially place-names, will appear to be mis-spelled. This may be because a spelling acceptable to everyone has been hard to establish; or it may be because I have adopted some nineteenth-century spellings in order to be consistent with those used in the quoted extracts (e.g. ‘Kistna’ for ‘Krishna’, ‘Siwaliks’ for ‘Shivaliks’, ‘Ganges’ for ‘Ganga’, etc.). I trust that purists will show indulgence and that all the names are at least recognisable. In the case of the Bengali genius ‘Radhanath Sickdhar’, the spelling is that which he himself used, however improbable it now looks.
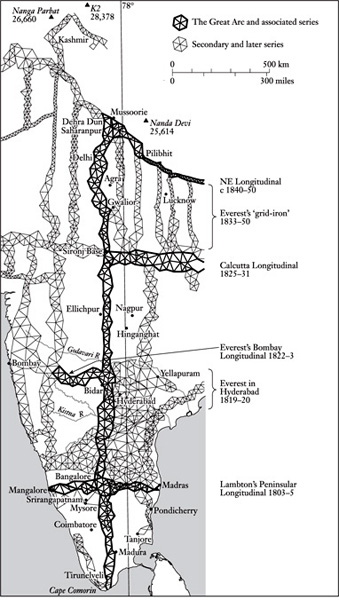
THE GREAT ARC AND ASSOCIATED SERIES
Foreword
Pressed about why Mount Everest is so named I would once, perhaps like most people, have come up with the explanation that it was as good a name as any. For a geographical feature of such obvious permanence and precedence, ‘Everest’ seems to say it all. Up there, more aloof from the bustle of life than anywhere else on earth, the raised snows proffer a pledge of peace, a promise of lasting repose, of being ‘ever-at-rest’. Presumably some international body had ordained the name; or perhaps it was a translation of the mountain’s local title. It scarcely mattered. Either way, it was perfectly acceptable.
But, as I now know, these suppositions were totally wrong. That the world’s highest point is in fact called after George Everest, a controversial British Colonel who had never even seen the mountain, let alone climbed it, first dawned on me when I was writing a book about the exploration of Kashmir. Everest did not feature in the region, either as man or mountain, but an institution, dear to the Colonel’s heart and known as the Survey of India, did. Most of Kashmir, including the Karakoram mountains, had first been measured and mapped by men of the Indian Survey. And the Survey being a government department within British India’s bureaucratic Leviathan, it had generated copious records. To these I turned.
Descriptions of nineteenth-century map-makers hauling their instruments up peaks of unknown altitude proved excellent value. Pelted by hailstones, their tents ablaze from the lightning and their trail obliterated by blizzards, the men of the Survey would dig in and wait. Survival depended on merino drawers, Harris tweeds and alpaca overcoats. Their boots were leather, and they ate mostly rice. They might be marooned for weeks. Then, without warning, in the chill first light of a day when the cloud had unaccountably overslept in the valleys, their patience would at last be rewarded. Sailing a sea of cumulus beneath an azure sky, a line of glistening summits would loom remotely from the ether.
With luck, from two or more of these summits tell-tale pinpricks of light would advertise the presence of other survey teams. If the theodolite was up and ready, sightings would be taken, bearings recorded and signals exchanged. The job was done. A speedy retreat down to the fleshpots of basecamp followed. Then it was on and up to the next peak.
Or so it seemed; but taking such bearings enabled the surveyors to plot the positions and heights of the distant peaks only if the location of their own peak was already known. Otherwise it was like seeking directions from a street map without first having identified your whereabouts. Fixing the positions of the other peaks depended on knowing that of the one from which one observed; its global location in terms of the world’s grid of longitude and latitude had to have been established, and so did its height above sea-level.
Obviously this information could have been obtained from prior observations taken at other vantage points in the rear. And those vantage points could in turn have been similarly established from somewhere in the foothills. But the Himalayas were hundreds of miles from any observatory capable of supplying a fix from astronomy; and they were even further from the sea, in terms of whose mean-level heights were expressed. Working back, then, somewhere there had to have been a starting point, a benchmark series of locations whose co-ordinates and heights had been deduced with a superior precision and were known with unimpeachable certainty.
I asked around, I dug out books, and the trail led back to the Great Arc – or, to give it its full title, ‘the Great Indian Arc of the Meridian’. I had never heard of it; but the Arc was indeed that benchmark series of locations. It was like the trunk of a tree, the spinal column of a skeleton. It ran for 1600 miles up the length of the subcontinent; and on the inch-perfect accuracy of its plotted locations all other surveys and locations depended.
Clearly, too, the Great Arc was something rather special. The mathematical equations involved in its computation seemed to fill enough volumes to line a library, while the instruments used to gather the raw data were man-size contraptions of cast iron and well-buffed brass which were still lovingly displayed in the Survey of India’s offices.
I ferreted further and I read on. Evidently the Great Arc was way ahead of its time. No scientific undertaking on such a massive scale had previously been attempted. Outside the regulated confines of Bourbon France and Georgian Britain, it was also the most minutely accurate land measurement on record. The accuracy was all-important because the Arc had as much to do with physics as with surveying. It was not simply an attempt to measure a subcontinent but also, incredibly, to measure and compute the precise curvature of the globe.
More prosaically, it was conceived by an elusive genius called William Lambton and was inspired by the first British conquests in the extreme south of India. The year was 1800. In North America Meriwether Lewis and William Clark had yet to set out on their epic journey across the continent. Australia was barely a penal colony; Napoleon still held Egypt; and most of the rest of Africa remained shrouded in that mysterious ‘darkness’ which was simply Europe’s ignorance.
Only in Asia, and especially India, was an embryonic imperialism detectable. Already the infant was outgrowing the womb of trade, stretching and kicking prodigiously, and taking its first unsteady strides towards dominion. Just so the Great Arc. Mirroring the progress of empire, it would forge tentatively and then inexorably inland. During forty years of high-risk travel, ingenious improvisation and awesome dedication it would come to embrace the entire length of India. And when Lambton, its endearing founder, died in central India, it would be carried to its grand Himalayan finale by the bewhiskered and cantankerous martinet who was Colonel George Everest.
At the time the scientific world was frankly amazed. The Arc was hailed as ‘one of the most stupendous works in the whole history of science’. It was ‘as near perfect a thing of its kind as has ever been undertaken’. Lambton and Everest ‘had done more for the advancement of general science than … any other body of military men’. Their celebrity was assured. Lambton was internationally fêted. George Everest was knighted by Queen Victoria; and in his honour that peak, whose discovery and measurement the Arc had made possible, was duly named.
Yet today they are utterly forgotten. Lambton is not even among the fifteen thousand worthies included in Chambers’ Biographical Dictionary. Everest is just a mountain. The progress of nineteenth-century invention was such that their science was almost instantly superseded. It now features only in histories of cartography, in academic critiques of imperialism, and in the dusty records of the Indian Survey. The Great Arc, like the great auk, has been consigned to oblivion.
Which is a pity, for it deserves better. At a time when to foreigners India was more a concept than a country, a place of uncertain extent and only fanciful maps, the Great Arc and the surveys based on it were indeed tools of imperial dominion as well as scientific enterprises. But thanks to that voluminous documentation and to George Everest’s published memoirs, the story of the Great Arc transcends both its science and its politics. Uniquely for an official scientific venture, we can savour the setbacks, share the excitement, discern the personalities. In writing this book the challenge has not been that of embroidering bare facts with vivid shades of plausible detail but of stitching into the riot of authentic adventure a thread of scientific and political plausibility. Given half a chance, jungle mishaps would have put paid to the science, personal vendettas would have obliterated the politics, and the tigers would have made off with the narrative.
If the impression given is less that of a scientific set-piece and more of a monumental example of human endeavour, then so it was. Travelling India with an eye on the Arc, I found it impossible not to become obsessed by the sheer audacity of the enterprise. Like Mount Everest, which seen from afar looks a respectable peak but not obviously the world’s highest, so the Arc viewed from a distance of two hundred years looks impressive but slightly quixotic. Get up close, though, breathe the sharp air and sense the monstrous presumption, and the Arc like the mountain soars imperiously to dwarf all else. Measuring the one, like climbing the other, is revealed as the ultimate challenge of its age.
ONE A Baptism of Fever
The word ‘jungle’ comes from India. In its Hindi form of jangal, it denotes any area of uncultivated land. Indian jungles are not necessarily forested, and today less so than ever. But well away from centres of population there do still survive a few extensive and well-wooded jungle tracts, especially in eastern and central India. Often they are classed as game sanctuaries, a designation which implies few facilities for the visitor but some much-advertised protection for the wildlife.
Here tigers and elephants yet roam, hornbills flap about in the canopy like clumsy pterodactyls, and hump-backed boar rootle aggressively through the leaf mould. In the dry season a safari might seem an attractive prospect. But be warned: ‘dry’ is high-baked. Like splintering glass, dead leaves explode underfoot to alert the animals. The tracks of crumbled dirt are hard to follow, spiked with ferocious thorns, and spanned by man-size webs patrolled by bird-size spiders.
The wet season is worse still. Then, the vegetation erupts. The tracks become impassable, and the air fills with insects. Only fugitives take to the jungle in the monsoon. Fugitives and, in days gone by when maps were rare, surveyors. In the year 1819, in just such a tract between the Godavari and Kistna rivers in what is now the south-eastern state of Andhra Pradesh, an English Lieutenant, lately attached to the Great Trigonometrical Survey of India and uncommonly keen to make his mark, underwent a baptism of fever.
Matters had gone badly for the twenty-eight-year-old Lieutenant from the start. Barely a month into this, his first season in the field, he had been confronted by a mutiny. ‘The infliction of corporal punishment is an odious task,’ he noted. But it was either that or abandoning the assignment. His escort obviously knew the perils of the monsoonal jungle and had seized every chance of escaping from the camp back to the city of Hyderabad. Something had to be done. Not without misgivings, the Lieutenant ordered one of these defaulters to be thrashed, whereupon the whole troop, about forty in number, took up their weapons and announced that they would decamp en masse. The British bluff had been called; in this insignificant and still today unfashionable corner of the subcontinent the myth of empire was at stake.
As might be inferred, by 1819 the British were already well on their way to becoming masters of India. Some areas had been won by conquest and were now under direct British rule; others were merely attached by treaty and remained nominally independent states under their own rulers. This was the case with the large principality of Hyderabad, through whose densest jungle the Kistna and Godavari rivers converged on the coast. Special permission had been obtained for the Great Trigonometrical Survey to operate in Hyderabad; but in ‘a native state’ the standards of subservience exacted in areas under direct British rule could not be taken for granted.
In fact, they could seemingly not be taken at all other than at the point of a gun. The mutineers, who now repaired to the nearby shade of a mango orchard, comprised a detachment of local troops lent by Nizam Sikander Jah of Hyderabad to protect and assist the British survey. In addition, the Survey had its own escort of twelve men who had been recruited in British territory, were paid out of the Survey’s budget and had already amassed many years of loyal service. This in-house escort was now ordered to load muskets and take aim at the mutineers. A volley into their midst was threatened if they did not immediately surrender.
The ploy worked. The mutineers submitted, and this time the Lieutenant offered no apology for calling for the cane. Three men were publicly flogged, then dismissed; and thus, the Lieutenant tells us, ‘was settled, very early in my career, a disputed point which had been a source of constant contention and annoyance to Colonel Lambton ever since his entering into the Nizam’s territory’.
Colonel Lambton was the originator and now Superintendent of the Great Trigonometrical Survey of India. For seventeen years he had been spinning a web of giant geometry across the Indian peninsula without ever having had to thrash any of its teeming peoples. Tactful, patient and indestructible, Lambton seemed immune to India’s frustrations, the result of a long wilderness experience in North America and of an attachment to science so obsessive and disinterested that even his critics were inclined to indulge him. Colonel Lambton beguiled India; but Lieutenant George Everest, his eager new assistant, chastised it.
The name, incidentally, was pronounced not ‘Ever-rest’ (like ‘cleverest’), but ‘Eve-rest’ (like ‘cleave-rest’). That was how the family always pronounced it, and the Lieutenant would not have thanked you for getting it wrong. Years later a fellow officer would make the mistake of calling him a ‘Kumpass Wala’. No offence was meant. ‘Kumpass Wala’, or ‘compass-wallah’, was an accepted Anglo-Indian term for a surveyor. Everest, however, accepted nothing of the sort. He detested what he called ‘nicknames’ and, though it was not perhaps worth a dawn challenge, he demanded – and received – abject apologies. Getting on the wrong side of George Everest was an occupational hazard with which even British India would only slowly come to terms.
With the mutiny quelled and the mutineers ‘finding that, when they knew me better, good behaviour was a perfect security against all unkindness’, a self-righteous Everest pressed on for the jungles beside the Kistna. It was July, the month when the monsoon breaks. On time, the heavens duly opened just as he climbed a hill to his first observation post.
Survey work was conducted during and immediately after the monsoon because, regardless of the discomfort, it was only then that the dust was laid and the heat-haze dispersed. In the interludes of bright sunshine, the atmosphere was at its clearest; in fact it became so transparent that Everest fancied he could see forever and that ‘the proximity of objects was only to be judged by their apparent magnitudes’. Trigonometrical surveying depended on the sighting of slender signal posts over distances of more than twenty miles. The monsoon’s perfect visibility was therefore ideal. Spying a long dark ridge all of sixty miles to the east, Everest despatched his four best signalmen to occupy its heights. The ridge, he understood, was called Panch Pandol, and the signalmen were to erect their flagpole there in readiness for his observations. Meanwhile he continued south to the Kistna with the rest of his party.
Although visibility was greatly enhanced by the monsoon, mobility was not. Dry riverbeds instantly became raging torrents full of uprooted trees. The Musi, a tributary of the Kistna, rose so rapidly that Everest found himself cut off from his supplies. On iron rations therefore, and denied the normal crossing on the Kistna, which was on the other side of its confluence with the Musi, he headed downstream to where an alternative ferry was said to operate at a spot about fifty miles above the modern city of Vijayawada.
The Kistna, one of India’s mightiest rivers, was now thrashing dementedly over steeply shelving rock like a panic-stricken patient beneath the surgeon’s knife. Crossing it meant trusting oneself to a coracle, a small circular vessel, more bowl than boat, made of woven rattans and faced with hide. Everest likened it to a leather basket. Such craft, still used in many parts of India, are highly portable and sometimes formed part of a surveyor’s outfit. Although not so provided, Everest found one abandoned by the river.
While it was undergoing the necessary repairs at the hands of the village cobbler, Everest ordered his ‘carriage-cattle’ to be swum across the flood. Fortunately they were not actually cattle, ox-carts being useless in roadless jungle, but a species he deemed ‘more at home in the water than any other quadruped’, namely elephants. As he also noted, elephants are extraordinarily sagacious. The Survey’s beasts duly swayed to the bank, took a long look at the rocks and the raging waters, assessed the mix of caresses and curses on offer, and opted to stay dry. ‘Probably it was fortunate,’ Everest adds, ‘for these powerful animals … are, from the size of their limbs, in need of what sailors term sea-room, and in a river like the Kistna … were very liable to receive some serious injury.’
This reverse meant a change of plan. Dr Henry Voysey, one of Everest’s two British companions and the Survey’s geologist-cum-physician, was left on the north bank with the main party plus elephants, horses, tents and baggage. Meanwhile Everest and a dozen men, balancing the Survey’s cumbersome theodolite between them, crossed to the other side. Three trips had to be made; and since the coracle had to undergo repairs after each, it took most of the day. Then, deceived by the visibility into thinking it was only a couple of miles away, Everest immediately set out for his next observation post.
The couple of miles turned out to be twelve. They included both jungle work and rock-climbing. By the time the hill of Sarangapalle was reached it was dusk, and big black clouds, aflicker with lightning, were piling up overhead. ‘At last,’ noted Everest, ‘when all their batteries were in order, a tremendous crash of thunder burst forth, and, as if all heaven were converted into one vast shower-bath, the vertical rain poured down in large round drops upon the devoted spot of Sarangapullee.’
Tentless in the deluge, Everest and his men bent branches to make bivouacs. His own was improved by a bedstead and an umbrella, between which he slept the sleep of the utterly exhausted, oblivious alike of his squelching tweeds, puddled bedding and benighted followers. ‘These evils might have been borne without any ill effects,’ he insists, ‘but for other circumstances of more serious consequence.’
The natives of India, according to Everest, ‘with their minds bowed down under the incubus of superstition’, attributed all fevers to witchcraft, and ignored natural causes. He, on the other hand, while amused by the idleness and absurdity of these doctrines, knew better. Malaria and ‘typhus’ fevers were alike the result of ‘a poisonous influence in the air’ which emanated from moist and ‘unwholesome’ soils. Under the impression that he was contributing to medical research, he examined the different schists and shales, the crystalline sandstone of Sarangapalle, the blue limestones of the Kistna and the porous sandstone of the Godavari in minute detail. These, he believed, were the ‘other circumstances’ which would prove of such serious consequence for his survey.
At the time most of his contemporaries shared these medical views. But, in a nice case of geographical coincidence, Hyderabad would host a further attempt to discover the natural causes of malaria. Seventy years later in a house in Begampet, now a suburb of Hyderabad city, Surgeon Ronald Ross would experiment on the insects of the Kistna-Godavari jungles and trace the malaria parasite to the anopheles mosquito. Everest’s ideas of ‘malarial vapours’ would thereby be exposed as every bit as idle and absurd as those of his followers.
After observing from Sarangapalle, he recrossed the Kistna and rejoined his camp to head north towards the Godavari. On the way he conducted observations to prominent hills like that to which he had earlier sent his signalmen. The survey on which he was engaged was what was known as a ‘secondary triangulation’. It was intended to cover all the country between the Kistna and the Godavari with a network of imaginary triangles whose sides connected intervisible observation posts.
Triangulation means simply ‘triangle-ing’, or conceiving three mutually visible reference points, usually on prominent hills or buildings, as the corners of a triangle. Knowing the exact distance between two of these points, and then measuring at each the angles made by their connecting sight-line with those to the third point, the distance and position of the third point can be established by trigonometry. One of the newly determined sides of this triangle then becomes the base for a second triangle embracing a new reference point whose position is determined in the same way. Another triangle is thus completed and one of its sides becomes the base for a third, And so on. A web, or chain, of triangles results; and Everest’s job was to extend this web of triangulation over the whole Kistna-Godavari region.



