
Полная версия:
Базовая оценка минерализации. Ресурсный геолог

Базовая оценка минерализации
Ресурсный геолог
Андрей Вяльцев
Георгий Кирьяков
Моей жене Татьяне и моим дочерям Эмилии и Оливии, без которых эта книга была бы завершена на год раньше.
Андрей Вяльцев
Моим учителям в школе, институте и жизни: Афанасьевой А. И., Большаковой Г. Н., Салову Л. А., Горштейну А. Е., Пертелю А. И., Калабину Н. В.
Георгий Кирьяков
Дизайнер обложки Татьяна Вяльцева
© Андрей Вяльцев, 2024
© Георгий Кирьяков, 2024
© Татьяна Вяльцева, дизайн обложки, 2024
ISBN 978-5-0062-3285-3
Создано в интеллектуальной издательской системе Ridero
ВВЕДЕНИЕ
Введение в «умной» книге обычно самая понятная и легко читаемая ее часть. Мы постарались немного изменить этот старинный красивый обычай и сделать весь текст максимально понятным и не очень снотворным. Очень надеемся, что это у нас получилось. Хотя, безусловно, в некоторых местах мозги напрягать придется, что может вызвать приступ неудержимой зевоты. Но тут уж увы – так со всеми книгами, чуть более сложными, чем «Буратино».
Начнем с того, о чем эта книга. Эта книга посвящена основам трехмерного моделирования месторождений твердых полезных ископаемых. Хочется сразу подчеркнуть: именно твердых, причем «традиционных» – руд черных, цветных и драгоценных металлов. Ни один из авторов книги не имеет никакого опыта в моделировании жидких или газообразных полезных ископаемых. Поэтому если вам надо моделировать что-то нефтегазовое или месторождение подземных вод – боимся, в этой книге вы не сможете найти очень много полезного.
По нашему мнению, в любом сложном вопросе главное – понимание его сути, а не бездумное заучивание формул и определений. Именно поэтому формул в книге не очень много, а те объяснения, которые приводятся, зачастую далеки от строгого научного освещения рассматриваемых вопросов, но зато данные объяснения построены таким образом, чтобы была понятна суть. По крайней мере, мы старались сделать их такими.
Что касается инструментов. В мире существует довольно большое количество специализированного программного обеспечения для моделирования и статистической обработки данных. Мы постарались излагать материал без «привязки» к какому-либо конкретному программному обеспечению, хотя более опытные читатели без труда смогут заметить скриншоты из наиболее распространенных прикладных программ для моделирования. Тем не менее все, что здесь изложено, может быть приложено к любому существующему программному обеспечению (мы так думаем!).
Теперь о том, для кого предназначена эта книга. Нам кажется, что книга будет полезна геологам, которые начинают заниматься моделированием месторождений. Или уже начали, но ушли не очень далеко от начала. Или ушли далеко, но некоторые начальные моменты все равно не очень поняли. Также нам кажется, что книга может быть полезна студентам геологических специальностей вузов. К сожалению, в настоящее время геологические вузы дают не очень большую базу по вопросам моделирования, а в том, что дают, нередко присутствуют пробелы на довольно важных местах. Данная книга предназначена (в том числе), чтобы эти пробелы максимально сократить.
В случае, если вы постараетесь читать материал не совсем «по диагонали» и попытаетесь делать задания, которые приведены в данной книге, нам кажется, что у вас есть неплохой шанс овладеть следующими навыками:
– проводить статистический анализ данных опробования полезных компонентов;
– выполнять декластеризацию и композитирование;
– определять уровни аномальных («ураганных») содержаний;
– подготавливать данные опробования к интерполяции;
– определять изменчивость содержаний в зависимости от направлений;
– правильно подбирать модели вариограмм (или хотя бы не совсем наобум);
– подбирать настроечные параметры для интерполяции содержаний;
– производить оценку содержаний методами ближайшего соседа, обратных расстояний, обычного кригинга и индикаторного кригинга;
– сопоставлять исходные данные опробования с оценкой в блочной модели;
– производить классификацию минерализации согласно кодексу JORC.
Книга создана на основе учебного курса, который можно найти на широко известном обучающем ресурсе Stepik1. Если книга покажется интересной – милости просим и туда. Книга – штука неизменяемая, а в учебном курсе что-то может быть изложено по-другому – понятнее или глубже.
Примеры файлов и тренажеры, используемые по ходу книги, расположены на GitHub2.
Да, чуть не забыли. Кратко об авторах. Авторы настоящей книги – геологи, более 10 лет занимающиеся моделированием месторождений непосредственно в добывающих организациях. Основная часть того, что мы намоделировали за свою профессиональную жизнь – это месторождения золота и цветных металлов. Те примеры, которые встречаются в книге, либо взяты непосредственно из нашей практики, либо созданы «по мотивам» реальных ситуаций.
Авторы выражают благодарность Некрасову Андрею за вычитку книги, устранение ошибок и внесение рациональных предложений по ее дополнению.
Если в ходе изучения изложенного материала у вас возникнет недопонимание прочитанного и/или горячее желание что-то переспросить или возразить – добро пожаловать в telegram-канал «Ресурсные геологи3». Мы, скорее всего, где-то там присутствуем.
ГЛАВА 1. СОЗДАНИЕ И ОБРАБОТКА РУДНОЙ ВЫБОРКИ
Рудная выборка
Что это – «рудная выборка»?
Рудную выборку можно определить как часть данных опробования, которая характеризует «возможно рудную» часть геологического пространства, моделируемую зону минерализации. Рудная выборка – это единственный источник для оценки содержания полезных компонентов в вашей модели. Пробы, по каким-либо причинам не включенные в рудную выборку, в оценке содержаний не участвуют.
Создание рудной выборки – очень важный шаг в процессе моделирования. Рудная выборка – это основа вашей будущей модели. Ошибки, сделанные на этом этапе, скорее всего, приведут к ошибкам в модели и вполне могут создать проблемы при обработке данных.
Способ формирования рудной выборки зависит от выбранной методики моделирования. В данной главе будем считать, что моделирование выполняется способом, который является наиболее часто используемым, а именно – с помощью построения каркасов минерализации. Необходимо сделать замечание, что каркасное моделирование – отдельная большая тема и в книге не рассматривается.
В описанном случае рудная выборка – это те пробы, которые находятся внутри каркасов минерализации. При этом не все пробы, попавшие в каркасы, могут входить в рудную выборку.
Причин, по которым проба в пределах каркасов может быть исключена из рудной выборки, масса. В качестве примера можно привести:
– проблемы при проходке выработок, приведшие к низкому выходу материала проб (например, низкому выходу керна). Тут также возможны варианты: от попадания скважины в ослабленную зону разрывного нарушения до низкой квалификации персонала буровой;
– недоверие к данным опробования, полученным в предыдущие периоды. Чаще всего такая неприятность случается с «историческими» данными, полученными несколько десятилетий назад;
– несоответствие выбранного способа опробования геологическим особенностям месторождения – например, бурение слишком малым диаметром на месторождении с высокой локальной изменчивостью (например, на месторождениях с крупным видимым золотом);
– неудачная схема опробования, не соответствующая моделируемому объему. Например, зачастую на месторождениях, разведанных в 40-50-е годы прошлого века на Северо-Востоке России, опробование месторождений выполнялось бороздовым способом по подземным выработкам и только по наиболее «интересной» части – по визуально видимой жиле или зоне прожилкования. А зона околорудных изменений либо не опробовалась вовсе, либо опробовалась по сильно разреженной сети (или вообще 5-7-10 проб на весь объект). В итоге такой схемы опробования мы имеем огромную массу бороздовых проб, освещающих только богатую часть минерализации и редкие пробы, дающие отдаленное представление о качестве измененных пород за пределами визуально выделяемого оруденения (и которые показывают вполне себе промышленные содержания по нынешним временам). В принципе, и в более позднее советское время (60—70—80-е) бороздовые пробы на месторождениях, отрабатываемых подземным способом, были крайне популярны. Да, в позднее время бороздами старались осветить всю мощность зоны минерализации, но даже в этом случае опробовать то, что осталось «за стенкой» подземной выработки, физически невозможно. При интерполяции по такой выборке «в лоб» мы неизбежно получим существенное завышение содержаний. Поэтому при такой ситуации приходится как-то выкручиваться, в том числе и исключая пробы из рудной выборки. В ряде случаев приходится поступать как в той сценке: «здесь играть, здесь не играть, здесь я рыбу заворачивал» – т. е. использовать бороздовые пробы при оконтуривании, но не использовать при интерполяции (или использовать фрагментарно).
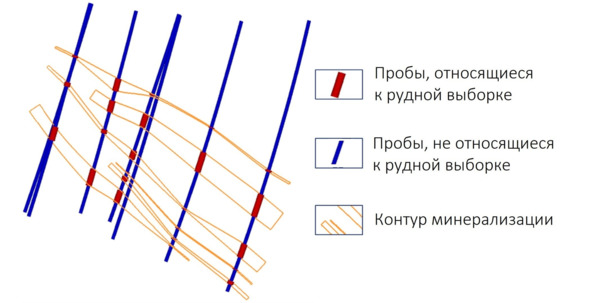
Рудная выборка
Оценку содержания в вашей будущей модели вы будете выполнять только по рудной выборке. Все пробы, которые остались за пределами каркасов минерализации, а также пробы, попавшие в каркасы, но исключенные из выборки, сколь бы «интересными» содержаниями они ни характеризовались, на качество вашей модели оказывать влияние не будут.
Этапы формирования рудной выборки
Рудная выборка – это важная часть ваших отчетных материалов. Практически это один из «китов» моделирования. Отсутствие рудной выборки в составе материалов моделирования – случай нередкий и очень печальный. По сути, отсутствие возможности понять, по каким данным выполнена оценка, кардинально снижает «ценность» модели (например, в этом случае невозможно достоверно сказать – использованы ли данные за тот или иной период разведки для построения модели или нет). Процесс моделирования должен быть «прозрачным» для любого, кто работает с моделью: у такого специалиста должна быть возможность понять, по каким данным выполнена оценка содержаний. Да, в общем, не исключен вариант, что этим специалистом будете вы сами через N месяцев. Неужели вы считаете, что будете помнить все аспекты моделирования? Или, может, вы настолько не любите себя, что не хотите облегчить жизнь себе из будущего?
Необходимо отметить следующий важный момент: пробы, исключенные из рудной выборки, в обязательном порядке также должны быть освещены в отчетных материалах с четким обоснованием причин исключения. Причина «что-то она мне не понравилась» вряд ли может считаться приемлемой.
К моменту формирования рудной выборки в вашем распоряжении уже есть каркасные модели минерализации. В каркасах может присутствовать поле зонального контроля, т. е. индивидуальный номер рудного тела или домена, а может и не присутствовать – опять же, зависит от выбранной методики моделирования. Методика построения каркасов в данной книге не рассматривается – как уже было сказано, это отдельная большая тема. Просто давайте будем считать, что каркасы минерализации вы уже построили, вы их проверили, и вы в них уверены.
«Стандартные» этапы формирования рудной выборки включают в себя:
– Выборка проб каркасами минерализации или кодирование проб каркасами (зависит от используемого программного обеспечения).
– Композитирование проб.
– Определение необходимости декластеризации и собственно декластеризация (если нужна).
– Определение необходимости урезки аномальных содержаний («ураганов»).
– Прочие трудно формализуемые манипуляции с рудной выборкой.
Каждый шаг должен сопровождаться анализом результатов этого шага. Крайне не рекомендуется «шагать вслепую», то есть выполнять следующий шаг, не оценив и не проанализировав результат сделанного. Такие действия рано или поздно приведут к тому же, к чему может привести прогулка с завязанными глазами – либо вляпаетесь во что-то нехорошее, либо вовсе куда-нибудь провалитесь.
Забегая немного вперед: все этапы моделирования, а не только создание рудной выборки, должны быть «прозрачными» – то есть стороннему наблюдателю должно быть «видно», что и как вы делали с вашими данными. Поэтому каждый шаг моделирования (в том числе и создание рудной выборки) должен сопровождаться прилагаемым результатом шага. То есть выбрали пробы каркасами – файл необработанной выборки сохранили в составе отчетных материалов. Композитировали – композитированная выборка отправляется в отчетные материалы. Урезали – аналогично. И то же самое с каждым этапом моделирования.
Выборка проб каркасами минерализации
Выборка/кодирование проб каркасами минерализации, в принципе, довольно простой шаг и в большинстве ПО выполняется с помощью нескольких «взмахов мышкой», тем не менее напомним о важных моментах в этой процедуре:
1. Если в каркасах минерализации присутствует номер рудного тела (рудной зоны, рудного домена), то выбор/кодирование проб каркасами должен выполняться с учетом этой особенности каркасов – т. е. в рудной выборке это поле также должно присутствовать.
2. При использовании номера рудного тела перечень номеров в рудной выборке должен совпадать с таковым в рудных каркасах. То есть количество и номера рудных тел в рудной выборке должны полностью соответствовать таковым в каркасах минерализации. Если внезапно в рудной выборке номеров рудных тел оказалось меньше, чем в каркасах, это, скорее всего, свидетельствует о проблемах с каркасами. Как бы вы ни были уверены в корректности последних, проверить их еще раз будет нелишним.
3. Крайне желателен визуальный анализ выбранных проб в сочетании с каркасами минерализации на предмет необоснованных изменений залегания тел или непонятных «подвесок» – вполне возможно, что в этих участках есть какая-то неприятность с каркасом.

Рудное тело и соответствующая ему рудная выборка. В рудной выборке нет ни одного интервала, на который бы опирался обведенный угол рудного тела. Очевидно, здесь какая-то проблема
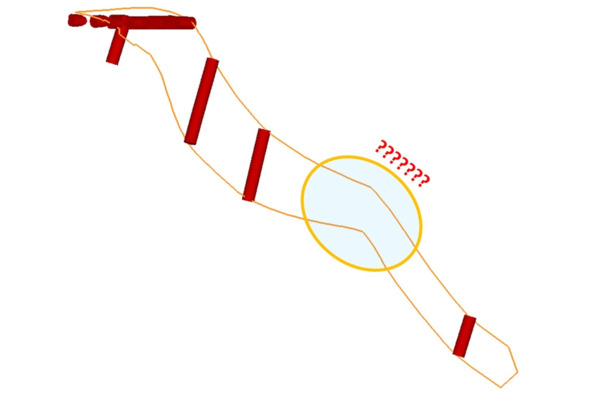
Неясна причина обведенного «колена». Вероятно, и здесь какая-то неприятность – почему-то интервал (который здесь, очевидно, должен быть) выпал из рудной выборки
4. Также нелишним будет произвести анализ количества выработок, освещающих каждое рудное тело. Схема проверки примерно следующая:
– Составляется список номеров рудных тел. Если моделирование велось с использованием каркасов, лучше всего такой список составить именно на основе каркасов.
– Для каждого номера рудного тела выполняется подсчет количества выработок, освещающих данное тело. Если в результате подобной проверки обнаружатся рудные тела с нулевым количеством выработок, это однозначно ошибка (это может быть как ошибка в данных опробования, так и ошибка в каркасах – тут уж ищите причину сами). В случае наличия номеров, для которых количество выработок равно 1, необходимо напрячь память и вспомнить, присутствовали ли в ваших каркасах линзы, опирающиеся на единичные пересечения.
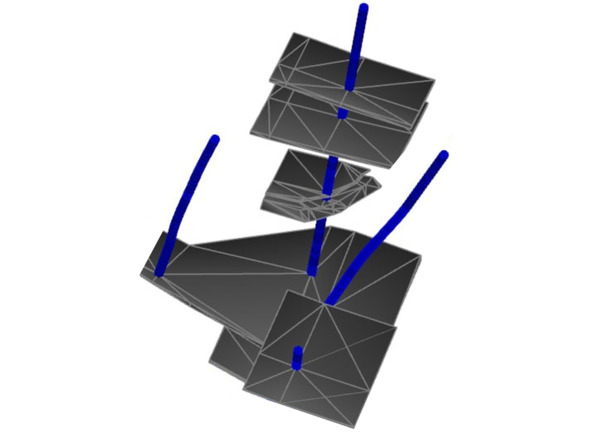
Линзы на единичных пересечениях
Если вы таких линз не строили, а тела с числом выработок равным единице присутствуют – очевидно, это тоже ошибка. Вообще, вопрос о целесообразности построения линз на единичных пересечениях – не самый однозначный. С одной стороны, этим мало кто занимается – возни много, толку мало: подобные линзы имеют низкую категорию достоверности и при технико-экономических расчетах обычно не используются. Кроме того, при нормальной степени разведанности месторождения на долю таких линз обычно приходится крайне незначительная часть ресурсов. И это при том, что оконтуривание таких линз должно выполняться по тем же принципам, что и оконтуривание «больших» тел – т. е. трудозатраты для их построения довольно значительны (а если считать трудозатраты «на единицу металла», значительно выше, чем для «больших» тел). Исходя из этого, кажется, что смысла в таких построениях почти нет. С другой стороны, подобная линза представляет собой цель для постановки доразведки: ну раз одна выработка что-то подсекла, давайте сгустим сеть – вдруг будет что-то интересное. И при редкой разведочной сети такое единичное пересечение может дать рудное тело неплохого размера, что, в свою очередь, может изменить перспективы того или иного локального участка (а если дело происходит на фланге рудной зоны – то может и не локального). В общем, решение о том, стоит ли возиться с подобными случаями, принимаете вы. Но мы бы рекомендовали при наличии времени постараться построить линзы хотя бы на наиболее «интересных» пересечениях, которые невозможно проследить.
5. Выбранные пересечения очень нелишне проанализировать на соответствие их используемым параметрам кондиций. В случае обнаружения пересечений, которые таким параметрам не удовлетворяют, будет полезным проанализировать причины попадания таких пересечений в контуры рудных тел (то есть это не обязательно ошибка).
6. Если вот совсем хочется помучиться, будет нелишним проанализировать рудную выборку на предмет «геометрического» соответствия каркасам: совпадают ли концы пересечений с узлами каркасов. По-хорошему должны совпадать полностью. Если вдруг обнаружилось, что это «не совсем так», стоит проанализировать причины такого несоответствия.
Краткое резюме
1. Рудная выборка – та часть данных опробования, которая характеризует моделируемую зону минерализации. Это единственный источник оценки содержаний в вашей модели.
2. Рудная выборка – это не просто исходные пробы, характеризующие минерализацию. Это пробы, которые подверглись всем тем трансформациям, которые вы посчитали необходимым произвести с исходными данными: выборка, композитирование, декластеризация, исключение отдельных групп проб, урезка ураганных содержаний и т. д.
3. Отчетные материалы должны отражать все манипуляции с пробами для получения рудной выборки. При этом в отчетных материалах должны присутствовать результаты всех сделанных вами шагов обработки:
– Вы выполнили выборку проб каркасами рудных тел – файл проб, выбранных каркасами, отправляется в состав отчетных материалов.
– Вы решили, что та или иная группа проб (или отдельные пробы) не должна участвовать в оценке содержаний – файл рудной выборки с исключенными пробами отправляется в состав отчетных материалов (то есть это уже второй файл рудной выборки в отчетных материалах).
– Вы композитировали пробы на среднюю длину (вычислили вес декластеризации) – аналогично: результат в отчетные материалы.
– Вы урезали аномально высокие содержания… ну, вы поняли.
4. Отчетные материалы, не содержащие рудную выборку, «стоят» очень немного. Отчетные материалы также в обязательном порядке должны содержать обоснование всех манипуляций:
– Выполнили композитирование – приводите гистограмму (гистограммы), из которых следует, что длина композитирования выбрана верно.
– Выполнили исключение проб – очень внятно и подробно пишем, почему эти пробы не достойны носить гордое звание членов рудной выборки.
– Урезали содержания – приводим все необходимые графики, расчеты и, естественно, уровни урезки (авторам встречались довольно забавные случаи, когда в отчете приведены графики, расчеты, скриншоты и т. д., но таблицу с уровнями урезки исполнитель предоставить забыл).
5. Кроме всего прочего, рудная выборка – неплохой инструмент проверки ваших построений.
Рудная выборка – это основа вашей будущей модели. В отношении нее в полную силу действует стандартное правило «мусор на входе – мусор на выходе». Попытаемся пояснить эту неложную истину реальными примерами из собственной практики работ.
# Пример из практики
Месторождение золота. Минерализация представлена серией тел субмеридионального простирания с размерами ~300—400×150—200 м и средней мощностью около 30 м. Месторождение имеет довольно длительную историю освоения: оно изучалось начиная с 60-х годов прошлого века. В результате этих работ на площади месторождения была создана разведочная сеть с шагом 50×50 м (в центральной части). В текущем веке изучение продолжилось, и разведочная сеть была сгущена до 50×25 м и 25×25 м.
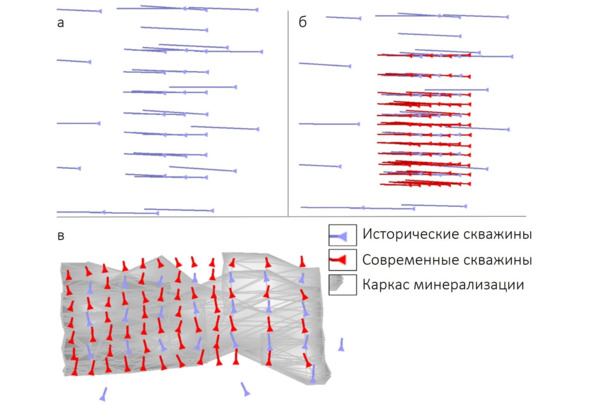
Разведочная сеть и зона минерализации. а – исторические скважины (вид в плане), б – исторические и современные скважины (вид в плане), в – 3D-проекция исторических и современных скважин с каркасами минерализации
Далее на основании всей имеющейся информации по опробованию было выполнено моделирование зон минерализации и запланированы добычные работы. При этом на некоторых участках, запланированных к первоочередной отработке, к моменту начала добычи разведочная сеть не была сгущена до 25×25 м. Внезапно при добычных работах был получен довольно ощутимый «неотход» металла на фабрике. Разница между «содержаниями по модели» и «содержаниями по факту переработки» составила -18%.
Возникли закономерные стандартные вопросы «Почему не выполнили?». И вот только на этом этапе у геологов появилось желание выполнить анализ данных, т. е. сопоставить данные исторического и современного бурения. По результам переработки сделали вывод, что причина неотхода кроется в ошибочной оценке содержаний, тогда как оценка количества минерализации выполнена верно.
Предположение о том, что исторические данные завышают содержания, было изначально проверено с помощью гистограммы, построенной по полному набору данных. Подобная гистограмма, к некоторому удивлению, наличие полимодальности не обнаружила. Разбивка полного набора данных на группы «исторические»/«современные» особой ясности не внесла.
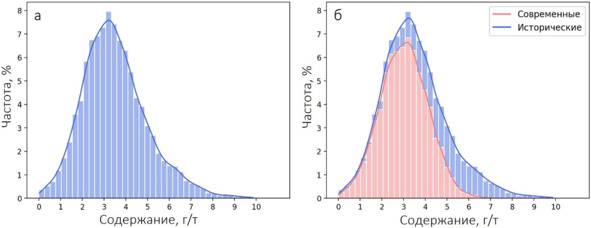
a – гистограмма по всему набору данных, б – гистограмма по всему набору данных с группировкой
Однако геологов не покидало ощущение, что что-то здесь не так. А что именно? Давайте посмотрим на гистограмму с разбивкой. Невооруженным взглядом видно, что исторических данных намного меньше, чем современных. Кроме того, если присмотреться чуть внимательнее, можно заметить некоторый рост количества исторических данных в области повышенных содержаний.
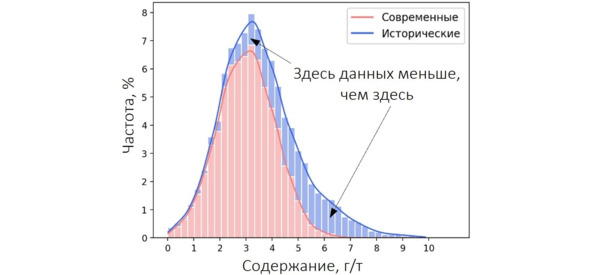
Гистограмма по всему набору данных с группировкой
При этом доли соответствующих данных рассчитаны от общего количества наблюдений (исторические + современные). Почему это важно? А потому, что при одинаковом масштабе отображения разницу между (условно) 50 и 30 на глаз видно прекрасно, между 5 и 3 – уже хуже, между 0.5 и 0.3 – намного хуже, а разницу между 0.05 и 0.03 вы на глаз не увидите, хотя соотношение между перечисленными величинами сохраняется. То есть чем меньше сравниваемые величины, тем сложнее их различить визуально. Давайте теперь построим ту же гистограмму, но без какого-либо смешивания выборок. И доли проб будем считать от количества данных соответствующего периода: доли исторических данных – в процентах от количества исторических данных, доли современных – в процентах от современных данных.
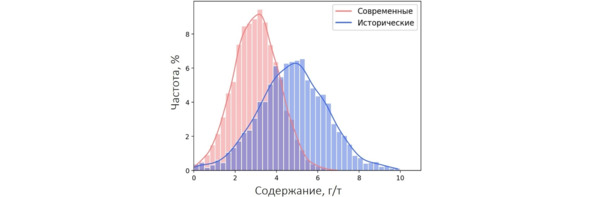
Гистограмма по двум наборам данных
Что тут скажешь… Полимодальность, однако. Давайте дополнительно посмотрим квантиль-квантильную диаграмму.
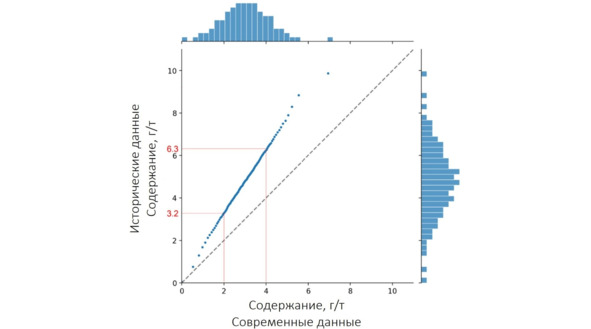
График квантиль-квантиль
Вот тут вообще красота: систематическое завышение содержаний в исторических данных по всему диапазону содержаний. В результате тяжких раздумий было принято решение выполнить полное перемоделирование месторождения, исключив из рассмотрения исторические данные. Закономерный финал: количество минерализации осталось почти тем же, а вот содержания упали довольно ощутимо. Неприятно, но это лучше, чем недополучение металла в процессе переработки. Вывод из описанного душераздирающего примера очень прост: получив в руки перед началом моделирования исторические данные, не поленитесь выполнить сравнительный анализ данных, полученных в разное время и/или разными способами. Иначе на вас запросто «повесят» недополученный металл. А оно вам надо?



