
Полная версия:
Цифровое моделирование на C#

Цифровое моделирование на C#
Дмитрий Павлов
Редактор Светлана Малышева
Корректор Светлана Малышева
Иллюстратор Дмитрий Павлов
Иллюстратор Анна Панкратова
Дизайнер обложки Анна Панкратова
© Дмитрий Павлов, 2024
© Дмитрий Павлов, иллюстрации, 2024
© Анна Панкратова, иллюстрации, 2024
© Анна Панкратова, дизайн обложки, 2024
ISBN 978-5-0062-8618-4
Создано в интеллектуальной издательской системе Ridero
Посвящается моей семье: моей жене Наталье, моим сыновьям Тимофею, Павлу и дочери Любови.
Предисловие
Моделирование – это процесс замены реального объекта его двойником с целью последующего изучения. Можно ли изучать непосредственно сам объект? Иногда можно, но даже в этих случаях мы часто, сами того не подозревая, переходим от объекта к модели. Например, перед нами стоит задача вычислить площадь стола. Для решения задачи мы подменяем стол его моделью – прямоугольником. А как вычислить площадь прямоугольника, мы хорошо знаем еще из школьного курса геометрии. В этом примере реальный объект – стол, мы заменили его абстрактной моделью – прямоугольником. Прямоугольник, как и стол, обладает свойствами, которые необходимы для решения нашей задачи: шириной и длиной. То есть модель всегда в некотором смысле похожа на реальный объект. Она должна обладать теми свойствами объекта, которые мы собираемся изучать или использовать.
С другой стороны, если мы захотим узнать, насколько прочен наш стол, наша модель (прямоугольник) становится бесполезной. Таким образом, модель всегда отражает лишь часть свойств реального объекта. Примеры, которые мы рассмотрели выше, конечно, очень просты. В реальных задачах выбор модели для изучения и ее создание, будь то изготовление копии на токарном станке или цифрового двойника на компьютере, может быть делом нетривиальным. И все-таки моделирование – это то, что упрощает, формализует процесс изучения окружающего мира, способствует эффективности и точности работы в различных отраслях. Благодаря моделированию можно изучать взаимодействие различных частей системы, анализировать их поведение и делать прогнозы. Моделирование помогает выявлять потенциально слабые места в системе, оптимизировать ее работу и принимать более взвешенные решения.
Благодаря всестороннему вхождению информационных технологий в нашу жизнь моделирование вышло на принципиально новый уровень. Экспоненциальное развитие вычислительных мощностей и постоянное совершенствование алгоритмов привели к возможности создания нового типа моделирования – компьютерного (цифрового). Цифровое моделирование – это процесс создания и использования виртуальных моделей для анализа, оптимизации различных систем и процессов, а также предсказания их поведения в ситуациях, связанных с реальной эксплуатацией. Цифровое моделирование позволяет создавать виртуальные модели объектов и систем, а затем использовать их для тестирования различных сценариев и принимать решения на основе полученных результатов. Цифровое моделирование дает возможность понять, как будет работать та или иная система еще до того, как эта система будет создана. С помощью этого подхода можно проводить краш-тесты автомобилей, реконструировать военные сражения, разрабатывать крыло самолета – и этот список ограничивается лишь нашей фантазией. Круг областей, где могут использоваться цифровые модели, очень широк – это медицина, биология, транспорт, логистика, строительство, финансы и т. д. Кроме практических сфер и бизнеса цифровое моделирование может использоваться в естественных науках, например, в физике, чтобы заменить дорогостоящий эксперимент виртуальным.
Необходимые знания и навыки
Читателю для понимания материала необходимо следующее:
– базовые знания математики: большая часть теоретического материала этой книги не подразумевает знаний, выходящих за рамки школьной программы, однако для понимания некоторых глав следует знать о векторах, матрицах, умножении матриц, стандартных математических функциях, производной и интеграле. Если в процессе чтения та или иная теоретическая часть будет вам непонятна в силу пробелов в знаниях, то при первом чтении ее можно пропустить без ущерба для общего понимания;
– для работы с программами, которые поставляются вместе с этой книгой, желательно иметь начальный опыт программирования на C#: необходимо уметь пользоваться средой разработки, иметь представление о типах данных в. NET, классах, интерфейсах, коллекциях; уметь использовать операторы ветвления и циклы.
Как устроена эта книга
Эта книга представляет собой доступное введение в практические вопросы цифрового моделирования. В книге изложены теоретические и алгоритмические основы, связанные с построением цифровых моделей. Она ориентирована на старшеклассников, студентов, профессиональных разработчиков, а также на всех тех, для кого программирование, помимо всего прочего, является увлекательным хобби.
Книга состоит из десяти глав-уроков. На каждом из уроков мы разберем конкретную задачу, связанную с цифровым моделированием. Я ставил себе целью сделать так, чтобы каждый урок являлся замкнутым с точки зрения изложения материала. То есть для понимания урока N вам не потребуется изучение урока N-1. Таким образом, вы можете читать эту книгу в том порядке, в каком пожелаете.
Отмечу, что данная книга – прежде всего, практическое руководство, поэтому я постарался изложить материал так, чтобы у читателя возникло желание открыть на своем компьютере программы, которые поставляются вместе с этим изданием. Каждый урок этой книги содержит минимальный набор теоретических сведений, необходимых для начала работы над цифровым моделированием. В некоторых местах книги не удалось уйти от формальных определений, но они нужны для того, чтобы материал был как можно более самодостаточным.
Миссия
Книга призвана способствовать рождению идеи и побудить вас к самостоятельным исследованиям, а также дать вам интересные примеры для вдохновения.
Дополнительные материалы
Вместе с этой книгой вы получаете доступ к программам, которые написаны на C# и демонстрируют практические аспекты цифрового моделирования. Дополнительные материалы – это не просто отдельные кусочки кода, а детально проработанные проекты. В конце каждого урока вы найдете описание программ, которые являются практическим дополнением к его теоретической части.
Книга поможет вам в создании ваших собственных проектов, поэтому вы можете использовать код из дополнительных материалов как вам угодно. Если при копировании кода вы сделаете ссылку на это издание, я буду вам очень признателен.
Программы можно скачать по ссылке:
https://gitverse.ru/dmitrypavlov74/DMBook
или воспользуйтесь QR-кодом для перехода на сайт:

По ссылке ниже (кроме исходников) вы сможете скачать и скомпилированные примеры:
https://disk.yandex.ru/d/33V3WI3A3mjyTA
Обратная связь
Написание книги – дело непростое. Даже если книга успешно продается, понять, насколько она была полезна читателю, очень сложно, поэтому я буду благодарен за любую обратную связь. Вы можете писать мне на адрес электронной почты dmitrypavlov74@gmail.com. Я стараюсь оперативно отвечать на поступающие вопросы. Это касается не только самой книги, но и дополнительных материалов.
Об авторе
Павлов Дмитрий является большим энтузиастом языка C#. Работал в таких компаниях, как «Danfoss», «Intel». Сейчас трудится в компании «Ридан», где курирует центр технических компетенций в области теплофизического моделирования. По образованию математик, кроме этого, получил дополнительное образование в области машинного обучения. В свободное время ведет свое сообщество в социальной сети «ВКонтакте» https://vk.ru/digitalmodelsru, где занимается популяризацией программирования и математики. В настоящее время проживает в Нижнем Новгороде.
QR-код для перехода в сообщество:

Урок 1. Построение графиков функций. Элементы интерполяции
Построения на плоскости
Введение
Большую часть информации об окружающем мире человек получает от органов зрения. Часто визуальный анализ данных может быть намного эффективнее, чем разглядывание длинных колонок чисел. Рассматривая таблицу чисел (рис 1.1), не сразу удастся понять, с какими данными мы имеем дело. Но взглянув на кривую, построенную по этим данным, мы легко угадаем знакомую нам еще со школы параболу.
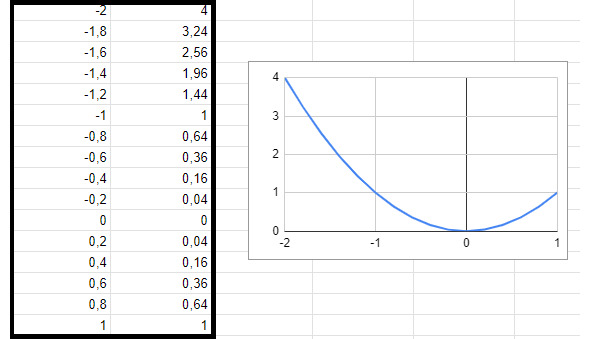
рис. 1.1
График функции представляет собой цифровую модель одномерных данных. С помощью этой модели у нас есть возможность лучше понять их природу, например, оценить интервалы монотонности и наличие экстремумов.
На этом уроке мы разберем одну из «вечных» задач – построение графиков функций. Мы научимся строить графики в декартовой и полярной системах координат, оптимизировать процедуру их построения; разберем особенности построения разрывных функций. Также мы узнаем, что такое интерполяция и разберем несколько ее видов.
Системы координат
Прежде, чем перейти к алгоритмам построения графиков, вкратце приведем некоторые сведения о координатных системах. В любой системе координат на плоскости точка задается парой значений (a, b). Каждая такая пара однозначно определяет место точки на плоскости. Обратное, вообще говоря, выполняется не всегда.
Декартова система координат
В декартовой системе координат, как правило, пары обозначаются (x, y), хотя это и не принципиально. Смысл значения x – это проекция точки на ось OX, y – это проекция на ось OY.
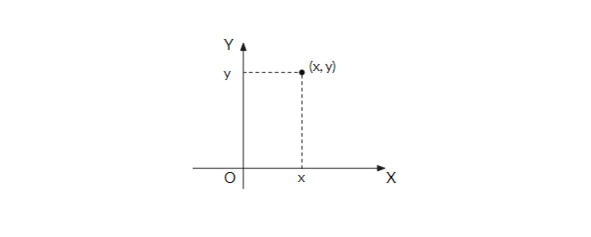
рис. 1.2
Полярная система координат
В полярной системе координат точки будем обозначать парой (r, t). Где r – это расстояние от точки О, называемой полюсом, а t – угол между горизонтальным лучом, исходящим из полюса, направленным вправо, и радиусом-вектором, указывающим на точку (рис. 1.3).
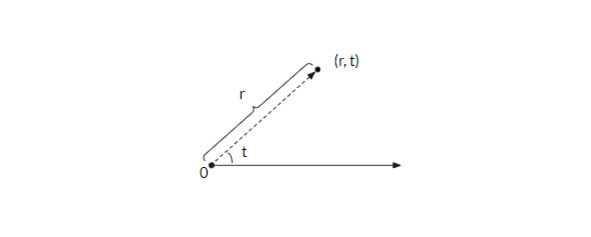
рис. 1.3
В ряде случаев полярные координаты оказываются удобнее декартовых. Например, для задания кривых на плоскости, особенно для задания различных спиралей, таких как спираль Архимеда, логарифмическая спираль, трилистника. Также полярная система координат используется:
– в астрономических наблюдениях;
– в фотографии – используют фильтр, переводящий координаты точек из прямоугольной системы в полярную, создавая сферический эффект снимка;
– в биржевых графиках – необычный формат на основе полярных координат предложил в 1990-е годы российский математик Владимир Иванович Елисеев;
– во взаимосвязи градусов и времени (в году 365 дней, в окружности – 360 градусов);
– в медицине – компьютерная томография сердца изображается в полярной системе координат;
– в системах безопасности при идентификации по радужной оболочке глаза.
Способы задания функций
Функции, заданные следующим образом y = f (x), называются заданными явно. Здесь y явно зависит от переменной x, а f определяет некоторое правило, по которому, взяв переменную x, можно получить y. При этом переменная x называется независимой переменной, а y зависимой. Или говорят, что y является функцией x.
Например: y = 2x + sin2x.
Функция может быть задана следующим образом:
x = X (t)
y = Y (t)
Здесь x и y являются функциями независимой переменной t. Такой способ задания функций называется параметрическим. Например, следующая пара функций определяет окружность радиусом 1:
x=cos (t)
y=sin (t)
Построение графика в декартовой системе координат
Для определенности мы начнем с построения графика функции, заданной явно в декартовой системе. Сформулируем шаги, необходимые для построения:
– Получить список точек в обычной системе координат.
– Получить список точек в компьютерной системе координат, преобразовав точки из обычной системы.
– Соединить получившиеся точки линией.
Ниже представлен пример кода, с помощью которого можно получить массив точек с координатами в обычной системе координат.
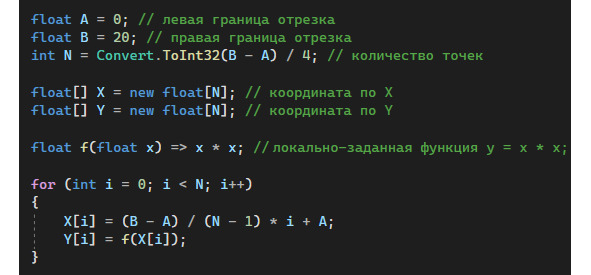
Код достаточно простой, но поскольку мы с вами находимся в начале пути, немного комментариев к нему не будут лишними. Во-первых, в коде присутствуют границы отрезка, на котором мы собираемся строим наш график – это A и B. Во-вторых, сама функция f (x) задана локально и в нашем случае это y=x2. От исходной функции требуется, чтобы она была определена при всех значениях внутри заданного отрезка. Очевидно, что наша функция этому условию удовлетворяет. Далее, N – это число точек для построения. На самом деле выбор этого значения – сама по себе весьма интересная задача. От выбора числа N зависит, как будет выглядеть наш график. Понятно, что нет смысла брать слишком много точек, поскольку разрешение экрана конечно. С другой стороны, точек не может быть мало, иначе график будет угловатым и не будет отображать истинное поведение функции. Обратите внимание на формулу для вычисления X [i]. При i=0, X [i] =A, а при i=N-1 (максимальной значение i в цикле), мы получаем X [i] =B. Поскольку формула для X [i] линейна относительно i, значит в массиве X будут лежать значения от A до B с равномерным шагом.
Согласно шагу 2, необходимо преобразовать данные из обычной системы координат в компьютерную. Экран монитора тоже представляет из себя декартову систему координат, с той лишь разницей, что ось Y здесь направлена вниз. Определим несколько величин:
[A, B] – отрезок, на котором задана исходная функция.
Ymax – максимальное значение функции на отрезке.
Ymin – минимальное значение функции на отрезке.
(X_win_min, Y_win_min) – левый верхний угол на экране монитора.
(X_win_max, Y_win_min) – правый верхний угол на экране монитора.
(X_win_min, Y_win_max) – левый нижний угол на экране монитора.
(X_win_max, Y_win_max) – правый нижний угол на экране монитора.
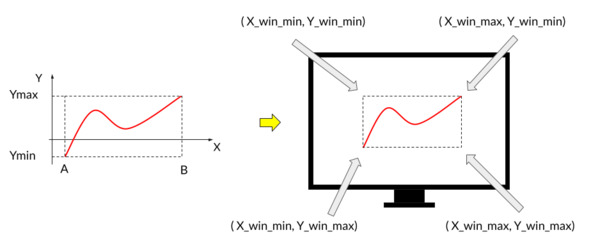
рис. 1.4
Теперь, когда у нас все готово, приведем формулы преобразования точек из обычной системы координат в компьютерную.
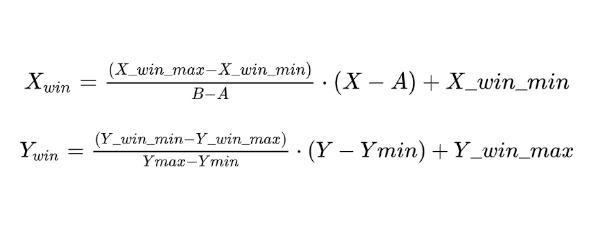
В данных формулах (X, Y) – это координаты точки в обычной системе координат, а (Xwin, Ywin) – координаты на экране монитора. Обратите внимание, что формулы не симметричны относительно осей X и Y. Как уже было упомянуто, это связано с тем, что компьютерная система координат устроена так, что ось Y направлена вниз, в то время, как в обычной системе эта ось направлена вверх. Данные формулы универсальны – используя их, можно вписать график любой функции в любой прямоугольник на экране. Тем не менее, все-таки есть очевидные ограничения на их использование. Во-первых, Ymax и Ymin должны достигаться на отрезке [A, B]. Существуют функции, которые не имеют максимума или минимума на заданном отрезке. Например, гипербола y=1/x не имеет ни того, ни другого на отрезке [-1, 1]. Ниже мы разберем как строить графики таких функций. Во-вторых, Ymax и Ymin должны быть различны, иначе в знаменателе мы получим ноль. Этот случай, впрочем, разрешается элементарно. Если у нас Ymax равен Ymin, то мы имеем дело с функцией y=const и в этом случае ее графиком будет просто горизонтальная линия.
Определим две функции, с помощью которых мы будем производить конвертацию.

Сама конвертация выглядит так, как показано на листинге ниже. В данном коде мы воспользовались функционалом, который предоставляет нам System.Linq для поиска минимального и максимального значений в массиве Y, а также для самой конвертации.
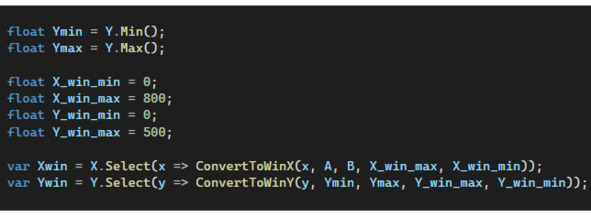
В переменных Xwin и Ywin теперь у нас лежит коллекция координат точек, которые мы соединим линией.
Построение графика в полярной системе координат
Для построения графика функции, заданной в полярной системе координат, мы сначала научимся конвертировать значения функции в декартову систему. Итак, пусть есть пара значений в полярной системе координат (r, t), давайте получим для нее соответствие в декартовой системе. Как видно из иллюстрации ниже, координата по оси OX равна произведению длины радиуса вектора r на косинус угла t, а по оси Y, соответственно, это произведение r на синус t.
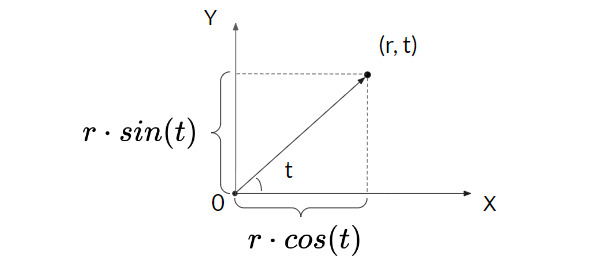
рис. 1.6
Таким образом получаем: x=r⋅cos (t), y=r⋅sin (t);
Сами формулы перехода достаточно просты. А поскольку мы теперь умеем переводить полярные координаты в декартовы, то можем считать, что мы успешно свели задачу к предыдущей.
Построение графика функции, заданной параметрически
Построение графика такой функции во многом схоже с построением функции, заданной явно. Более того, явное задание функции может быть сведено к параметрическому, а именно:
y = f (x) => X=t, Y=f (t)
Обратное преобразование от параметрического к явному не всегда возможно. В целом, как уже было сказано, построение графика такой функции не несет в себе принципиально иного подхода. Немного изменятся лишь функции конвертации значений из обычной системы в экранную.
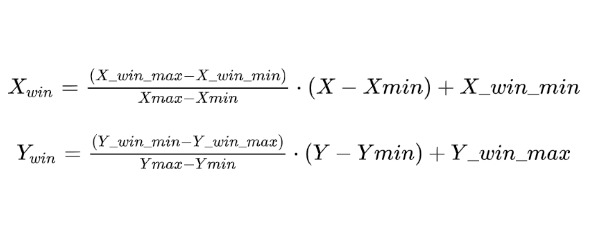
Как видим в формуле для X (преобразование по оси Y не претерпело изменений), величины A и B заменены на Xmin и Xmax соответственно.
Выбор N
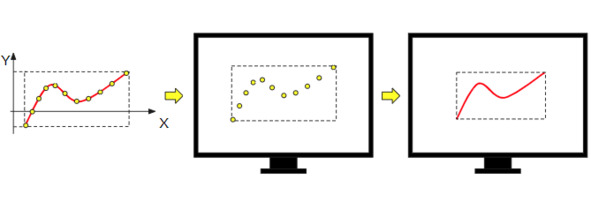
График может занимать маленькую часть на экране монитора или весь экран, но в любом случае мы хотим чтобы он был гладким и приятным для восприятия. Возникает вопрос: сколько требуется точек, чтобы график выглядел хорошо? Вообще число точек должно быть пропорционально длине графика. Исходя из этого, можно предложить следующий метод. Изначально мы берем довольно много точек в обычной системе координат, например, 10000. Далее конвертируем эти точки в экранную систему, а затем формируем новую коллекцию точек по следующему алгоритму – добавляем первую точку, а следующую точку добавляем с условием, что она отстает от предыдущей не менее, чем на 4 (например) пикселя. Получившуюся коллекцию соединяем линией. При таком подходе мы обеспечиваем приемлемый вид графика вне зависимости от того, сколько места он занимает на экране.
Оптимизация построения
Следуя вышеизложенному алгоритму, можно построить график, где точки, по которым мы его строим, следуют друг за другом с равномерным шагом. Однако часто такой подход не является оптимальным с точки зрения производительности. Например, известно, что в окрестности нуля функции y=sin (x) и y=x ведут себя почти одинаково. То есть синус очень похож на прямую, а прямую можно построить всего по двум точкам. Идея оптимизации состоит в том, чтобы там, где график близок к прямой, можно удалить лишние точки без потери качества. Далее мы разберем простой алгоритм, который на основе кривизны графика сможет уменьшать количество точек для построения.
Пусть точки p1 и p2 уже принадлежат списку точек, по которым строится график в экранной системе координат. Точку p3 включаем в этот список, только если ее отклонение от прямой, задаваемой точками p1 и p2, больше некоторой величины d.
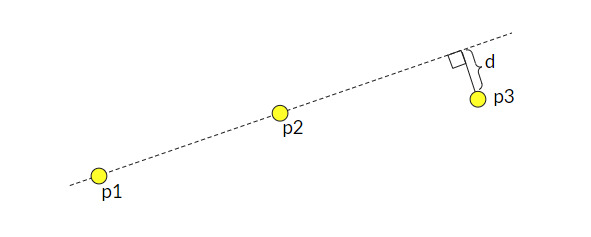
рис. 1.7
Определить расстояние от точки p3 (x3, y3) до прямой определяемой точками p1 (x1, y1) и p2 (x2, y2) можно по следующей формуле:
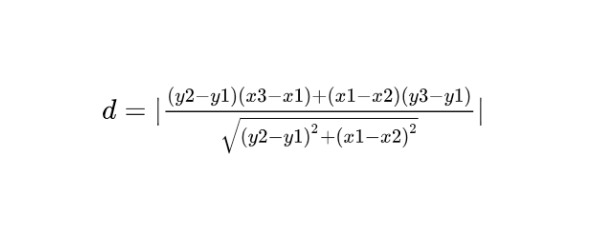
Такая простая модификация алгоритма построения позволяет уменьшить количество точек без потери качества отображения. Мы используем участки графика, где он близок к прямой, и на этих участках удаляем избыточные для построения точки.
На рисунке 1.8 мы видим график, построенный с равномерным шагом (без оптимизации).
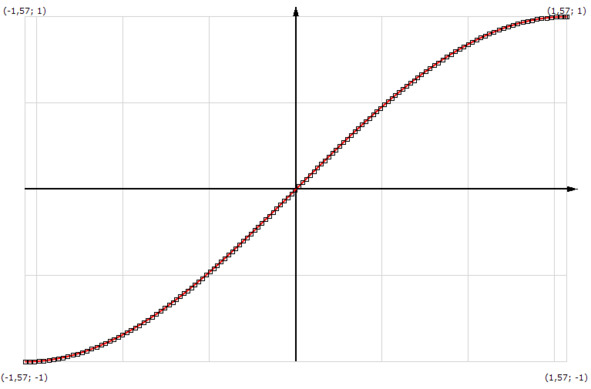
рис. 1.8
Число точек здесь равно 134. Сами точки отмечены квадратиками. Ниже представлен график той же функции, но к которому была применена вышеописанная процедура. График нисколько не потерял в качестве, а между тем число точек сократилось до 47.

рис. 1.9
Графики разрывных функций
Формулы, конвертирующие координаты точки из обычной системы координат в компьютерную, содержат минимальное и максимальное значения, которые достигает функция на отрезке. Для непрерывных функций эти величины обязательно существуют. Для разрывных функций это выполняется не всегда. По причине того, что минимум и максимум для разрывных функций могут не достигаться, использовать формулы, приведенные выше, нельзя.
Существует несколько типов разрывов функций. В данном разделе мы рассмотрим вариант построения графика разрывной функции с разрывом типа «скачок через бесконечность». Такой разрыв называется разрывом второго рода. Например, функция y=1/x на отрезке [-1, 1] как раз претерпевает такой разрыв в точке 0.
Чтобы научиться строить графики функций, имеющих разрыв, давайте попробуем понять поведение функции в окрестности точки разрыва. Как видно из рисунка ниже, при приближении к точке разрыва начинается быстрый рост приращения функции, при этом шаг по X остается фиксированным:
y2 – y1
Такое поведение функции указывает на то, что мы предположительно подошли к точке разрыва.
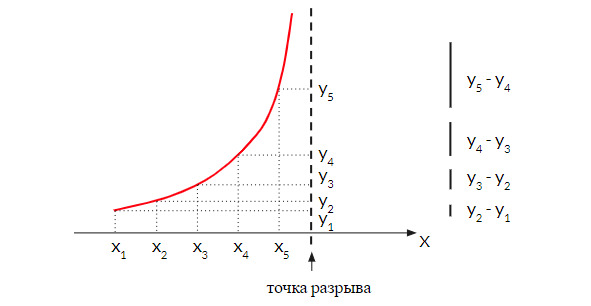
рис. 1.10
Необходимо вырезать из области определения точки разрыва вместе с некоторой окрестностью. После этого график функции распадается на две или более непрерывных кривых, заданных на участках, где точки разрыва отсутствуют. На каждом таком участке максимум и минимум будут достигнуты. Затем среди этих максимумов и минимумов нужно найти самое большое и самое маленькое значение и использовать их в качестве Ymax и Ymin, которые присутствуют в формуле для конвертации. Таким образом, мы снова сможем использовать формулы для конвертации точек из обычной системы в компьютерную.
Быстрый рост приращения функции в окрестности точки разрыва типа «скачок через бесконечность» является необходимым условием разрыва, но не достаточным. Можно привести пример функции, когда значение приращения будет сколь угодно велико, но тем не менее функция может оставаться непрерывной. Данный подход построения разрывного графика не является универсальным и подходит только для некоторых функций. Наиболее правильным было бы проанализировать аналитическое уравнение функции и найти, например, точки, где знаменатель обращается в ноль. Такие точки всегда являются точками разрыва, но не всегда относятся к типу «скачок через бесконечность».



