
Полная версия:
Статистический анализ взаимосвязи. Учебное пособие

Статистический анализ взаимосвязи
Учебное пособие
Валентин Юльевич Арьков
© Валентин Юльевич Арьков, 2020
ISBN 978-5-0050-4525-6
Создано в интеллектуальной издательской системе Ridero
Предисловие
Предлагаемое учебное пособие позволяет освоить базовые методы исследования взаимосвязей в пакете Microsoft Excel. Все действия описаны подробно, шаг за шагом, с примерами и комментариями. Попутно можно улучшить навыки работы в Excel, что само по себе уже полезно как элемент современной компьютерной грамотности.
Данное учебное пособие представляет собой второй выпуск серии «Бизнес-аналитика и статистика в Excel». При выполнении работы советуем использовать знания и навыки, полученные при изучении первого выпуска под названием «Анализ распределения в Excel». Рекомендуем изучать материал последовательно – и в рамках данной работы, и в рамках данной серии.
Мы будем использовать простые условные обозначения и названия:
– жирный шрифт – названия функций и пунктов меню;
– ЗАГЛАВНЫЕ БУКВЫ – выделение основных терминов и ключевых данных;
– КНОПКИ – кнопки на экране компьютера;
– КЛАВИШИ – клавиши на клавиатуре компьютера.
В тексте описана работа в текущей англоязычной версии Microsoft Excel из пакета Microsoft Office 365. Далее будем называть этот программный продукт просто Excel. При указании функций и пунктов меню мы будем давать оба варианта – на английском и на русском языке. На рисунках будем давать примеры англоязычного интерфейса.
Введение
Взаимосвязи между явлениями бывают самые разные. В данном выпуске мы будем рассматривать самый популярный вид взаимосвязи между случайными величинами, когда текущее значение одной случайной величины Y В СРЕДНЕМ определяется значением другой случайной величины X. Вокруг этого предсказуемого среднего имеется случайный непредсказуемый разброс. Лучше всего, если этот разброс постоянного размаха, то есть «сигма» разброса не меняется. Это так называемая КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ.
Эта две случайные величины называют по-разному:
X – факторный признак, фактор, независимая переменная, independent variable;
Y – результативный признак, результат, зависимая переменная, dependent variable.
На графике «иксы» откладывают по горизонтальной оси, а «игреки» – по вертикальной. В математике принято откладывать аргумент функции по оси X, а значение функции – по оси Y. В данном случае мы поступаем точно так же. Это намекает, что Y зависит от Х. Например, люди высокого роста в среднем весят больше. Поэтому рост можно будет обозначить через X, а вес – через Y.
Корреляционная зависимость изучается с помощью методов КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА. Кроме того, здесь мы снова проведём СВОДКУ И ГРУППИРОВКУ ДАННЫХ, но не для изучения распределения, а для анализа взаимосвязи.
Отчёт о работе оформляется по общим правилам, которые мы уже описали в первом выпуске серии и которые (как мы надеемся) уже удалось освоить в процессе выполнения заданий. Поэтому повторять рекомендации не будем, а сразу займёмся делом.
Общие сведения
В данной работе мы будем исследовать взаимосвязь между случайными величинами статистическими методами.
Мы познакомимся с одним из самых известных видов взаимосвязи под названием КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ, или просто КОРРЕЛЯЦИЯ. Можно сказать, что это «зависимость в среднем». Пример показан на рисунке ниже.
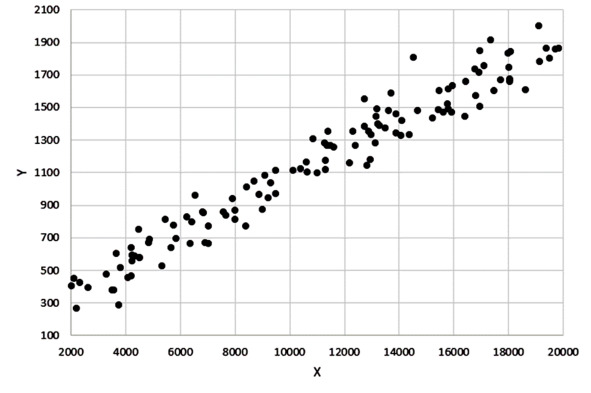
Корреляционная зависимость
На нашем рисунке видно, что с увеличением «икса» В СРЕДНЕМ увеличивается «игрек». Можно сказать, что здесь просматривается линия и разброс точек вокруг этой воображаемой линии. В этом случае говорят, что между «иксом» и «игреком» есть КОРРЕЛЯЦИЯ, или корреляционная зависимость, или корреляционная взаимосвязь.
Изображение того, как разбросаны точки по графику, называют по-разному:
– корреляционное поле;
– поле корреляции;
– диаграмма разброса;
– диаграмма рассеяния;
– «точечная диаграммма»;
– scatter plot.
Далее мы будем использовать название ДИАГРАММА РАЗБРОСА.
Корреляционная зависимость встречается в жизни. Вот некоторые примеры такой зависимости «в среднем»:
– рост и вес человека;
– площадь квартиры и её цена;
– уровень доходов и продолжительность жизни;
– доходы и расходы домашнего хозяйства;
– длина поездки и расход бензина;
– посещаемость занятий и оценка на экзамене.
Если рассматривать картину в целом, то здесь будет какая-то общая тенденция (прямая или кривая линия), а в каждом конкретном случае к ней добавляется случайный разброс, непредсказуемость, погрешность. По реальным данным можно оценить наличие (силу, степень, тесноту) взаимосвязи и даже построить уравнение такой зависимости. Такое уравнение даст нам только ориентир, среднюю картину и позволит делать приблизительные прогнозы.
Мы будем строить модель в виде одного уравнения, в котором есть один факторный признак и один результативный. Такая модель называется ПÁРНАЯ РЕГРЕССИЯ. Это означает, что у нас рассматривается ПАРА случайных величин, то есть в уравнении участвуют ДВЕ переменные.
Как и в предыдущей работе, вначале мы смоделируем исходные данные и познакомимся со статистическими методами. Затем мы возьмём реальные данные и применим к ним эти изученные технологии. Моделирование даёт идеальные, «красивые» данные, по которым можно начать обучение. Реальные данные всегда «угловатые», «шершавые», «некрасивые», неидеальные. Но это жизнь, и именно с реальными данными приходится иметь дело исследователям, инженерам, программистам, экономистам.
Модели описывают реальную жизнь очень приблизительно, но даже такое приближённое описание может быть полезно при решении реальных задач на производстве и в бизнесе. Слово ПРИБЛИЖЁННОЕ указывает, что есть некоторая погрешность и что наша модель, наше уравнение ПРИБЛИЖАЕТСЯ к реальной жизни. То есть близко, но не точно. И это уже лучше, чем полная неизвестность и неопределённость. А полной, абсолютной точности никогда не бывает. Даже на рынке можно поторговаться, и цена изменится, причём у разных покупателей получится по-разному. Так что, выходя из дома за покупками, человек только очень приблизительно может оценить предстоящие расходы.
Варианты задания
Варианты заданий представлены в таблице ниже. Здесь мы используем следующие условные обозначения.
X – факторный признак, или фактор, или независимая переменная. Мы моделируем Х как случайную величину с РАВНОМЕРНЫМ РАСПРЕДЕЛЕНИЕМ в указанном диапазоне.
E – случайная составляющая. Будем моделировать Е как случайную величину со СТАНДАРТНЫМ НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ, то есть с нулевым средним и единичной дисперсией.
Y – результативный признак, или результат, или зависимая переменная. При моделировании мы вычисляем Y по формуле, в которой участвуют фактор X и случайность E. Коэффициент при случайной составляющей определяет её СИГМУ (стандартное отклонение) и, соответственно, разброс вокруг среднего.
n – объём выборки. Это количество изучаемых объектов (статистических единиц), например, людей, квартир или жёстких дисков. У каждого объекта будут свои значения X и Y. Например, у каждого человека будет своя пара значений: роста и вес. Можно сказать, что в нашем случае объём выборки – это число строк в таблице с данными, или число записей в базе данных, или КОЛИЧЕСТВО ПАР случайных чисел {X, Y}. Для каждого объекта будет своя пара чисел Х и Y. В нашей работе объём выборки равен 200 для всех вариантов.
Оформление отчёта подробно описано в предыдущем выпуске серии. Создадим новую рабочую книгу. Сохраним отчёт в файле с коротким информативным названием. Сделаем титульный лист отчёта и заготовку оглавления.
В данной работе мы будем вначале рассматривать линейную функцию, а затем нелинейную. Соответственно, у нас имеется две таблицы с вариантами заданий.
Выберем свой вариант задания и опишем его на новом листе отчёта.
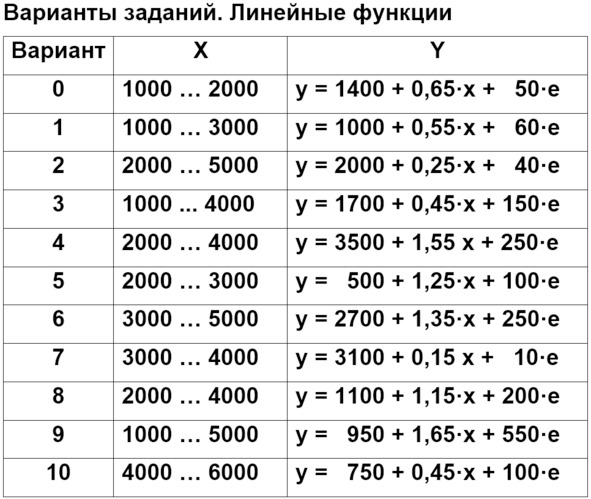
Зарисовка линейной функции
Вначале надо представить себе, что представляют собой наши данные, как будет выглядеть график. Для этого сделаем зарисовку на бумаге – как в предыдущей работе.
Нам предстоит изобразить расположение нашей линии и форму диаграммы разброса – в самых общих чертах.
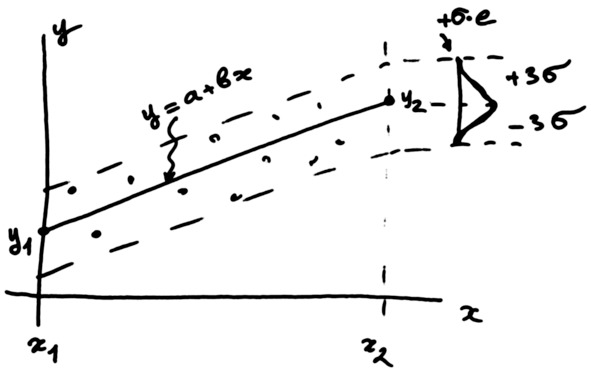
Зарисовка диаграммы разброса
Изобразим оси координат и займём нужное место на листе бумаги.
Масштаб на графике необязательно должен начинаться от нуля. Главное, чтобы диаграмма разброса занимала всё поле графика. Метки на осях – «красивые», круглые числа.
В нулевом варианте задания X изменяется в пределах от 1000 до 2000. По оси «икс» указываем крайние значения 1000 и 2000 в начале и конце оси.
Теперь оценим диапазон значений Y. Берём формулу для Y, пока без учёта случайности Е:
Y = 1400 +0,065 · X
Подставляем крайние значения X:
Y (1000) = 1400 +0,065 · 1000 = 2050
Y (2000) = 1400 +0,065 · 2000 = 2700
Выбираем масштаб по оси «игрек» от 2000 до 3000.
Получаем 2 точки, через них проводим прямую линию.
Добавим разброс вокруг линии. Для этого используем ПРАВИЛО ТРЁХ СИГМ: почти все значения случайной величины находятся в диапазоне «среднее плюс-минус три сигмы». Когда мы строим разброс вокруг линии, в роли среднего значения будет точка на линии.
В нулевом варианте случайный разброс равен 50 · Е. Случайная составляющая Е имеет единичную дисперсию. Сигма Е тоже будет равна единице, потому что сигма – это квадратный корень из дисперсии. Если умножить случайную величину Е на 50, то её сигма тоже увечивается в 50 раз. Стало быть, сигма равна 50, а три сигмы равно
3 · 50 = 150.
Вокруг первой и последней точек на графике строим разброс «плюс-минус три сигмы».
2050 – 150 = 1900
2050 +150 = 2200
2700 – 150 = 2550
2700 +150 = 2850
Проводим пунктиром две параллельные линии. Это будут границы случайного разброса.
Заполняем эту «полосу» точками – случайным образом.
Вот что мы ожидаем увидеть, когда смоделируем исходные данные – см. рисунок.
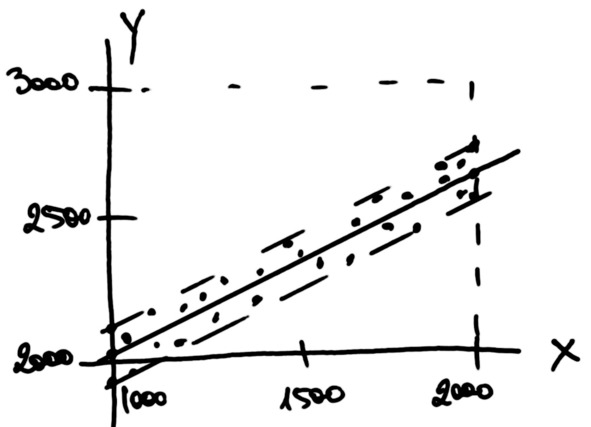
Зарисовка
Зачем в этой работе мы делаем зарисовку? При любых вычислениях нужно уметь ЗАРАНЕЕ ОЦЕНИВАТЬ и МЫСЛЕННО ПРЕДСТАВЛЯТЬ себе будущие результаты. Тогда сразу будут видны ГРУБЫЕ ОШИБКИ. И эти ошибки можно будет сразу же выявить и исправить. Ну а ошибки будут всегда.
Если не оценивать будущий результат, то можно легко сказать: «Это компьютер так посчитал». Проблема в том, что исходные данные вводит человек и результаты будет использовать тоже человек. Программу тоже написал человек, и не один. Поэтому ОТВЕТСТВЕННОСТЬ за результаты расчётов несёт не компьютер, а человек.
Зарисовка нелинейной функции
Вторая часть задания – это нелинейная функция второго порядка. Варианты заданий приводятся в таблице. Другие названия: квадратичная функция, парабола – см. формулу.
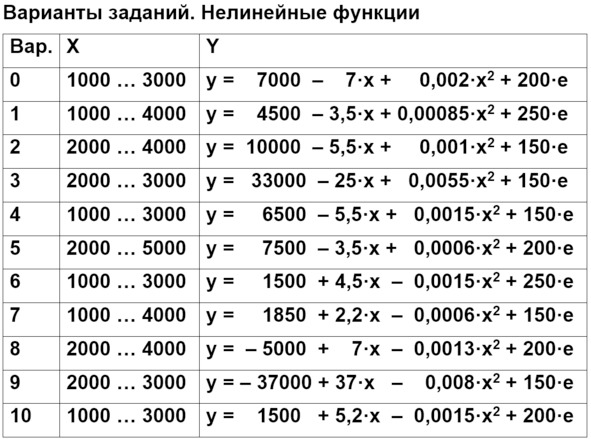
Уравнение параболы можно записать разными способами, поэтому нужно следить за тем, в каком порядке расположены члены уравнения.
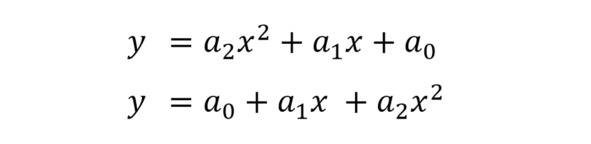
Уравнение параболы
В первом примере степени аргумента расположены по убыванию. Во втором – по возрастанию. Как записать уравнение – не так важно. Главное – правильно прочитать те результаты, которые нам выдаст программа.
На новом листе отчёта опишем свой вариант задания. Напомним, что мы в качестве примера рассматриваем нулевой вариант.
Пределы изменения факторного признака: от 1000 до 3000.
Уравнение функции:
y = 7000 – 7 · x +0,002 · x2 +200 · e
Коэффициенты уравнения:
a0 = 7000
a1 = – 7
a2 = 0,002
s = 200
Коэффициент при случайной составляющей E обозначим буквой S, поскольку он определяет значение «сигмы».
Чтобы сделать зарисовку параболы, нужно определить два основных момента.
Вначале определим знак старшего коэффициента при второй степени фактора a2. Если коэффициент a2 положителен, то ветви параболы напрaвлены вверх. И наоборот.
В нулевом варианте старший коэффициент равен
a2 = 0,002.
Коэффициент положительный, следовательно ветви параболы смотрят вверх.
Затем определим положение вершины параболы.
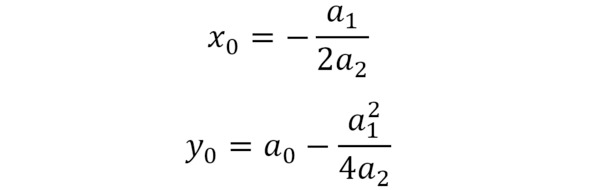
Вершина параболы
Докажите справедливость формул для нахождения координат вершины параболы, приравняв первую производную функции к нулю. Затем подставьте полученное значение х0 в уравнение параболы и упростите выражение.
Подставляем наши коэффициенты и находим координаты вершины – см. формулы.
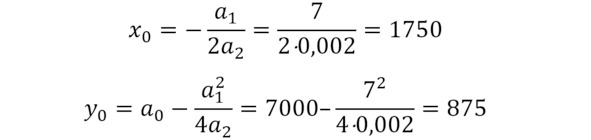
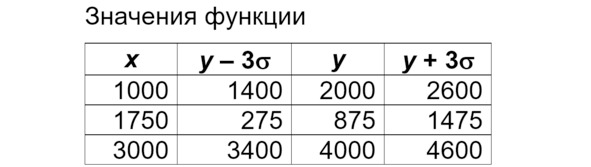
Координаты вершины
Далее определим значения функции на границах диапазона значений – см. формулы.

Крайние значения
И наконец добавляем границы случайного разброса по «правилу трёх сигм». Сигма в нулевом варианте равна 200, соответственно, три сигмы равно 600. Добавляем и отнимаем 600 в каждой из трёх точек – см. формулы.
Делаем зарисовку и вставляем в отчёт, как описано в предыдущем выпуске. Цель этого упражнения – представить общую форму графика, а не демонстрировать художественный талант или способности к черчению.
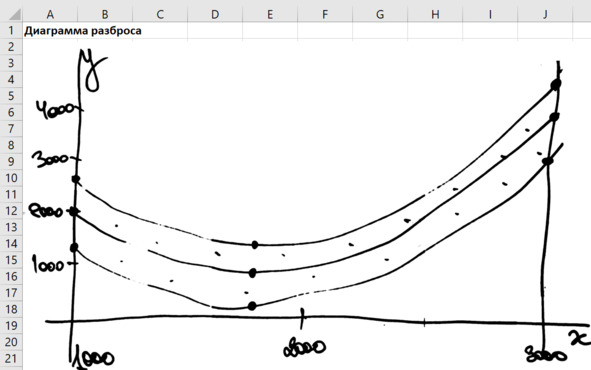
Зарисовка
Исходные данные
Сгенерируем исходные данные – значения двух переменных x и y – в соответствии c вариантом задания. В качестве примера разбираем нулевой вариант. Используем функцию
Random Number Generation
Генерация случайных чисел
надстройки
Data Analysis
Анализ данных.
Подробности использования генератора мы уже описали в предыдущей работе. Числа округляем до целых.
Создаём столбец случайных чисел X.
Распределение – Равномерное
Левая и правая границы – 1000 и 2000.
Начальное состояние – 1234. Можно взять любые другие числа, но их нужно зафиксировать в отчёте, чтобы не использовать второй раз.
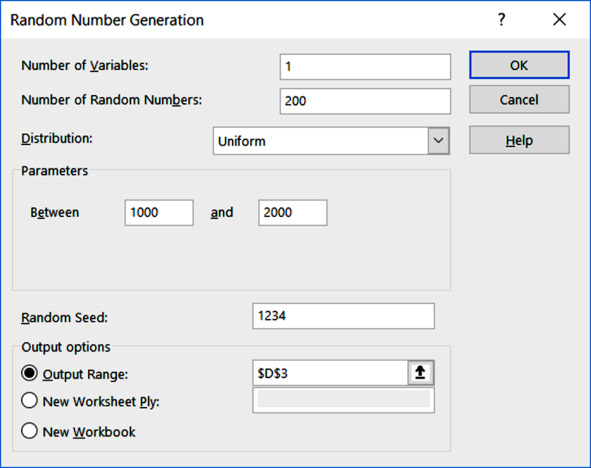
Настройки генератора
Полученные значения X округляем до целых и записываем в другой столбец. Для округления используем функцию
ROUND (number, num_digits)
ОКРУГЛ (число; число разрядов).
Обратим внимание, что в английской версии аргументы функции разделяют ЗАПЯТОЙ, а в русской – ТОЧКОЙ С ЗАПЯТОЙ. Причина в том, что в английской версии десятичный разделитель целой и дробной частей – точка, а в русской – запятая.
Пример результата генерации данных и округления можно видеть на рисунке ниже. В дальнейшей работе используются именно округлённые значения X и Y.
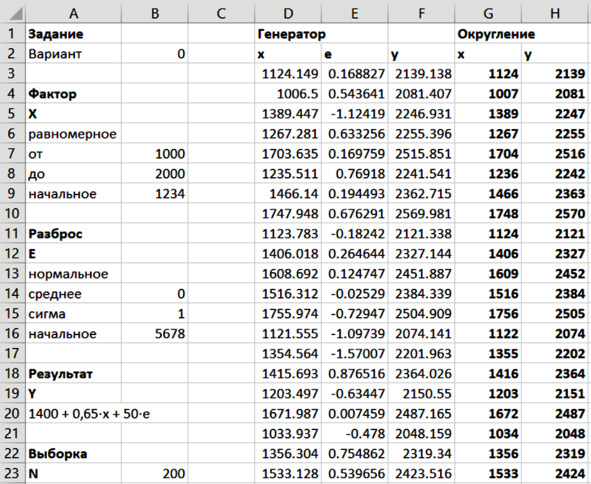
Сгенерированные данные
Вспомогательная случайная составляющая E поможет нам сформировать случайный разброс вокруг линии. Она имеет нормальное распределение с нулевым математическим ожиданием и единичным стандартным отклонением. Значения E следует сгенерировать в отдельном столбце с ДРУГИМ начальным состоянием генератора.
Программный генератор случайных чисел на самом деле создаёт ПСЕВДОСЛУЧАЙНЫЕ числа. Другими словами, они только кажутся случайными. Если задавать одно и то же начальное состояние генератора, мы получим одну и ту же последовательность «случайных» чисел.
Проведём опыт и убедимся, к чему приводят одинаковые настройки генератора. Сгенерируем столбцы Х и Е с одинаковым начальным состоянием генератора: 1234. Результат – на рисунке слева. Теперь сгенерируем Х и Е с настройками 1234 и 5678. Результат показан справа.
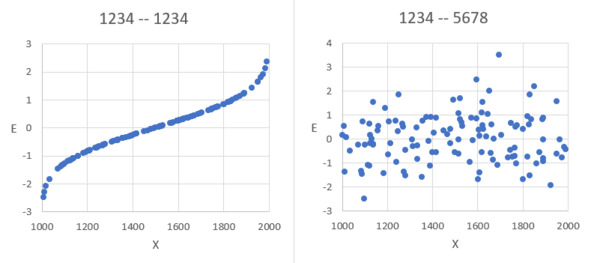
Влияние начального состояния
На левом графике можно видеть явную связь (точную функциональную зависимость) между случайными числами Х и Е – при одинаковой настройке генератора: 1234 и 1234. На этом графике просматривается кривая нормального распределения. Она используется для создания случайного числа с заданным распределением. Разные настройки 1234 и 5678 дают действительно независимые случайные числа. Учтём на будущее.
Выделим два столбца с готовыми данными – с заголовками. Вставим данные на новый лист. Выберем режим вставки значений из буфера обмена.
Вставка значений
При выборе режима вставки из буфера можно сразу увидеть результат на экране. Нажимаем кнопку
Values
Значения.
После вставки получаем числа вместо формул в ячейках таблицы. Теперь никакие наши действия не приведут к обновлению и изменению данных.
Диаграмма разброса
Пришло время посмотреть на график наших исходных данных. На диаграмме разброса каждая пара чисел Х и Y изображается отдельной точкой. Точки на графике НЕ СОЕДИНЯЮТ линиями. В примере «Рост – Вес» нет никакой связи между параметрами соседей по парте. Поэтому каждый человек – это отдельная точка на графике.
Выделяем два столбца с округлёнными значениями X и Y. Выбираем в меню:
Insert – Charts – Insert Scatter (X, Y) or Bubble Chart – Scatter – Scatter
Вставка – Диаграммы – Вставить точечную (X, Y) или пузырьковую диаграмму – Точечная – Точечная.
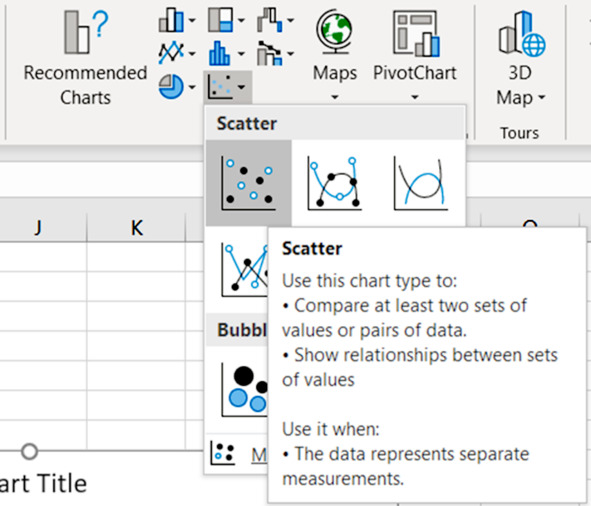
Вставка диаграммы разброса
По умолчанию диаграмма разброса выглядит не слишком привлекательно – см. график. Настроим оформление графика.
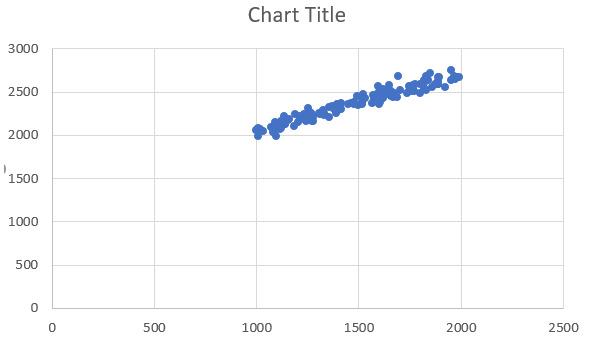
Диаграмма разброса по умолчанию
Настроим масштаб по осям, чтобы диаграмма заполняла всё поле графика. Дважды щёлкнем по горизонтальной оси. В диалоговом окне
Format Axis
Формат оси
выбираем раздел
Axis Options
Параметры оси.
Устанавливаем пределы по горизонтальной оси от 1000 до 2000.
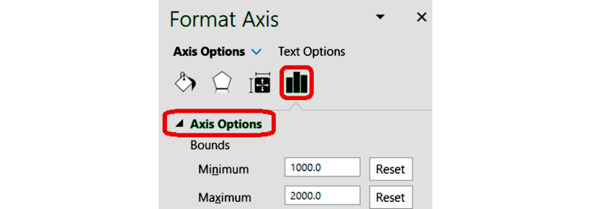
Масштаб по оси
Щёлкнем по вертикальной оси и выберем такие значения, чтобы диаграмма разброса занимала всё место на графике.
Теперь настроим заголовки. Щёлкнем по графику и нажмём на кнопку
Chart Elements
Элементы диаграммы.
Это квадратная кнопка с символом ПЛЮС справа вверху.
Элементы графика
Отмечаем пункт
Axis Titles
Названия осей.
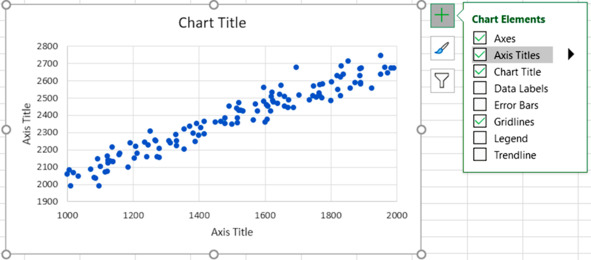
Заголовки осей
Отредактируем заголовки и укажем, где находятся наши «иксы» и «игреки». Для дальнейшего украшения развернём заголовок вертикальной оси на 45 градусов. Щёлкнем по заголовку вертикальной оси и выберем в меню:
Format Axis Title – Text Options – TextBox – Text Box – Text direction – Horizontal
Формат названия оси – Параметры текста – Надпись – Надпись – Направление текста – Горизонтально.
Далее установим чёрный цвет для точек-маркеров. Щёлкнем по маркерам и установим в меню чёрный цвет:
Format Data Series – Series Options – Fill & Line – Marker – Marker Options – Fill – Solid fill – Color – Black
Формат ряда данных – Параметры ряда – Заливка и границы – Маркер – Параметры маркера – Заливка – Сплошная заливка – Цвет – Чёрный.
Здесь же отключим обрамление маркеров:
Format Data Series – Series Options – Fill & Line – Marker – Marker Options – Border – No line
Формат ряда данных – Параметры ряда – Заливка и границы – Маркер – Параметры маркера – Граница – Нет линий.
После настроек диаграмма разброса должна выглядеть следующим образом – см. рисунок.
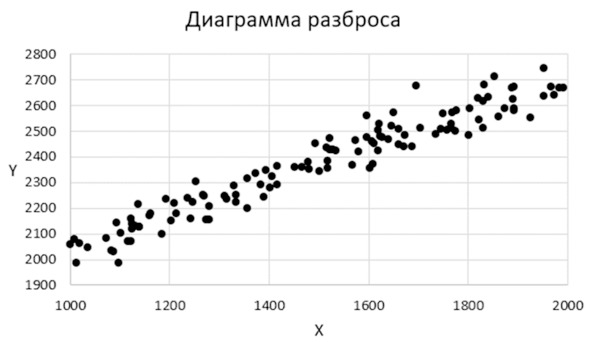
Оформленная диаграмма
Корреляционный анализ
Корреляционный анализ позволяет исследовать тесноту связи, то есть степень разброса точек вокруг линии. Чем ближе точки к линии регрессии, тем лучше ТЕСНОТА СВЯЗИ. Имеется в виду линия, которую МОЖНО построить в среднем по этом точкам. На самом деле при анализе взаимосвязи перед нами находятся только точки, а линии пока ещё НЕТ.
Теснота линейной связи оценивается с помощью КОЭФФИЦИЕНТА ЛИНЕЙНОЙ КОРРЕЛЯЦИИ r. Здесь говорится именно о ЛИНЕЙНОЙ связи и анализируется разброс вокруг будущей, возможной ПРЯМОЙ линии. Другими словами, мы выясняем, есть ли смысл в построении прямой линии в среднем по нашим точкам.
Коэффициент корреляции принимает значения от —1 до +1 включительно.
Знак коэффициента указывает на НАПРАВЛЕНИЕ связи – прямую или обратную связь. Положительная корреляция означает, что с увеличением фактора в среднем возрастает результативный признак. Это прямая связь. Отрицательная корреляция – это обратное направление связи, то есть снижение, убывание, падение графика. С увеличением фактора убывает результат.
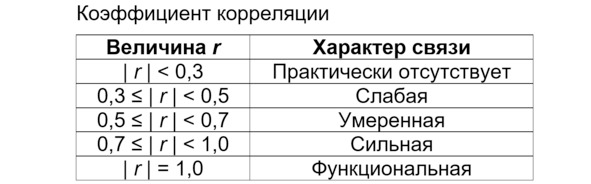
Величина (модуль, абсолютное значение) коэффициента характеризует ТЕСНОТУ линейной связи. Чем ближе значение к единице, тем меньше разброс, тем ближе точки к прямой линии. Чем ближе коэффициент к нулю, тем сильнее разброс вокруг прямой. Традиционное толкование величины коэффициента корреляции приводится в таблице.
Возможна и другая ситуация – НЕЛИНЕЙНАЯ зависимость, которая тоже представляет собой отсутствие линейной связи. Нелинейной зависимостью является всё, что не является линейным, например, кривая или ломаная линия. В этом случае коэффициент линейной корреляции будет близок к нулю. Но при этом точки могут быть очень тесно расположены вокруг кривой или ломаной линии. Для анализа степени нелинейной связи используют другие коэффициенты корреляции. В данной работе мы ограничимся только анализом тесноты линейной зависимости.



